저등급 열원의 변환을 위한 칼리나 사이클과 유기 랭킨 사이클의 엑서지 성능의 비교 해석
2020 The Korean Hydrogen and New Energy Society. All rights reserved.
Abstract
The organic Rankine cycle (ORC) and the Kalina cycle system (KCS) are being considered as the most feasible and promising ways to recover the low-grade finite heat sources. This paper presents a comparative exergetical performance analysis for ORC and Kalina cycle using ammonia-water mixture as the working fluid for the recovery of low-grade heat. Effects of the system parameters such as working fluid selection, turbine inlet pressure, and mass fraction of ammonia on the exergetical performance are parametrically investigated. KCS gives lower lower exergy destruction ratio at evaporator and higher second-law efficiency than ORC. The maximum exergy efficiency of ORC is higher than KCS.
Keywords:
Low-grade heat source, Organic Rankine cycle(ORC), Kalina cycle system(KCS), Ammonia-water mixture, Exergy키워드:
저등급 열원, 유기 랭킨 사이클, 칼리나 사이클 시스템, 암모니아-물 혼합물, 엑서지1. 서 론
재생에너지 사용의 확대는 지난 수십 년 동안 많은 나라에서 국가 중요 정책으로 다루어져 왔다. 현재 많은 국가와 국제기구는 재생에너지를 에너지 안보, 경제 개발, 환경 보호 및 온실가스 배출 감소 노력의 중요한 요소로 보고 있다1). 저등급 열원의 에너지를 전기와 같이 더 가치 있는 에너지 형태로 변환하는 방법으로서, 근년에는 유기 랭킨 사이클(organic Rankine cycle, ORC)과 칼리나 사이클 시스템(Kalina cycle system, KCS)이 가장 경쟁력 있는 시스템들로 평가되고 있으며, 이에 대한 많은 연구들이 수행되어 왔다2-4).
저등급 열원은 온도가 상대적으로 낮고 일반적으로 열이 전달됨에 따라 온도가 변하는 현열 에너지 형태로 공급된다. 물을 작동유체로 사용하는 전통적인 수증기 랭킨 사이클(steam Rankine cycle, SRC)은 열원 온도가 370℃ 이하가 되면 일반적으로 경제성을 잃는 것으로 알려져 있다5). ORC는 SRC와 구조는 기본적으로 같지만 작동 유체로서 물보다 비등점이 낮은 냉매나 유기물을 사용한다. ORC는 구조가 간단하고 신뢰도가 높으며, 다양한 열원에 대한 적응성이 좋은 점 등 장점들이 많다6-8). ORC의 경제성은 작동 유체의 열역학적 특성과 밀접하게 연관되기 때문에, 부적절한 작동 유체의 선택은 높은 경비와 낮은 효율로 이어질 수 있다9-11).
KCS는 암모니아-물 혼합물을 작동 유체로 사용한다. 암모니아-물과 같은 비공비 혼합물(zeotropic mixture)은 등압 조건에서도 온도가 변하면서 상변화가 일어나기 때문에 열전달에 따라 온도가 변하는, 현열 형태의 저등급 열원 유체와 작동 유체 사이에 열이 전달되는 과정에서 온도차의 불균형과 엑서지 파괴를 줄일 수 있어서 에너지 변환 효율을 높일 수 있다12,13). 그러나 암모니아-물의 혼합물을 작동 유체로 하는 랭킨 사이클은 팽창기에서의 고온 특성은 우수하나 작동 유체의 응축 압력을 낮추기 어려워 경제성이 떨어진다. KCS는 작동 유체의 기액 분리를 통해 고농도의 기체로 팽창기에서 팽창하면서 동력을 생산한 다음 저농도의 액체와 혼합해 작동유체의 농도를 낮추어 응축시키기 때문에 팽창기의 압력비를 높일 수 있어 시스템의 에너지 변환 효율이 우수하다14-16).
엑서지는 시스템의 상태가 주위 환경의 상태(사장 상태)로부터 벗어난 양의 척도로서, 시스템이 주어진 상태로부터 사장 상태까지 가역 과정으로 이행하는 동안 얻을 수 있는 최대 일 에너지 또는 유용도이다. 열역학 제2법칙에 기초한 시스템의 엑서지 해석은 에너지 해석을 보완해서, 시스템의 각 위치에서 파괴되거나 손실되는 유용 에너지의 크기와 원인에 대한 정보를 제공하므로 더 효과적인 에너지 자원 사용을 위한 해석에 적합하다17).
ORC나 KCS를 통하여 에너지를 변환하는 경우, 작동 유체의 선택이나 혼합물의 농도 설정, 열교환기의 용량 그리고 각 구성 요소의 운전 압력과 온도 범위에 따라 시스템의 효율과 경제성이 크게 달라진다18). 본 논문에서는 현열 형태의 저등급 열원을 사용하는 ORC와 KCS에 대하여 열역학 제2법칙에 기초하여 엑서지 성능을 비교 해석한다. ORC는 사용하는 작동 유체를, KCS는 암모니아 농도를 바꾸면서 터빈 입구 압력에 따라 주요 구성 요소에서 파괴되거나 손실되는 엑서지의 크기와 그 원인을 비교 분석하고, 이어서 시스템 전체 성능을 나타내는 엑서지 효율과 2법칙 효율의 변화에 대하여 조사한다.
2. 시스템 해석
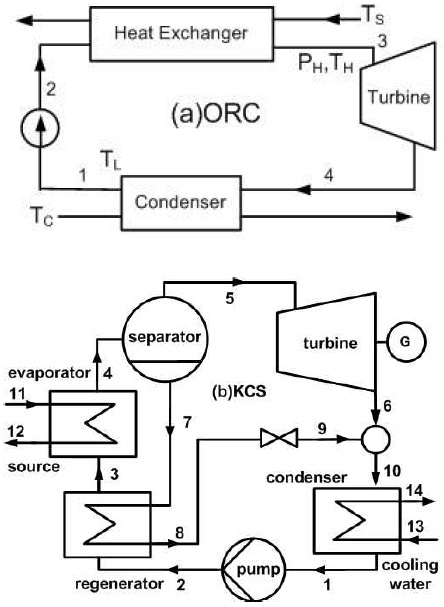
본 논문에서 해석하는 시스템의 모식도를 Fig. 1에 나타내었다. 유기 랭킨 사이클(ORC) 시스템은 증발기(열교환기), 터빈, 응축기 및 펌프 등으로 구성되며, 칼리나 사이클 시스템(KCS)은 증발기, 분리기, 터빈, 교축 밸브, 응축기, 펌프 및 재생기 등으로 구성된다.
본 논문에서는 효과적인 시스템 해석을 위해 다음과 같은 가정을 사용한다18,19): 1) 시스템은 정상상태로 운용된다. 2) 압력 강하는 펌프와 터빈에서만 생기고, 그에 따라 열교환기에서 유체의 압력은 일정하다. 3) 열교환기 내부 열전달을 제외한 열손실은 무시한다. 4) 펌프와 터빈의 등엔트로피 효율은 일정하다. 5) 터빈 입구에서 작동 유체는 순수 증기이며, 터빈 출구에서 작동 유체의 건도는 기준값 90% 이상을 유지한다.
열교환기는 고온 유체와 저온 유체의 최소 온도차가 주어진 핀치포인트온도차 ΔTpp가 되도록 운전된다고 가정한다18). 열원 유체의 질량 유량이 ms일 때 펌프에서 작동 유체의 질량 유량 mw와 응축수의 질량 유량 mc는 증발기에서의 에너지 균형으로부터 다음과 같이 구한다.
| (1) |
| (2) |
여기에서 cp는 정압 비열, T는 온도, h는 비엔탈피이며 하첨자 w, s, c, in, out은 각각 작동 유체, 열원 유체, 냉각수, 입구 및 출구를 나타낸다.
KCS에서 시스템의 유입열, 재생기 열전달, 시스템 출력 및 열효율을 각각 Qin, Qr, Wnet, ηth라 하면 각각 다음과 같이 구할 수 있다.
| (3) |
| (4) |
| (5) |
| (6) |
질량 유량을 m, 사장 상태를 하첨자 0으로 나타내면 엑서지 유량 E는
| (7) |
로 쓸 수 있다. 열역학 2법칙 효율 ηII와 엑서지 효율 ηex는 다음과 같이 정의된다.
| (8) |
| (9) |
증발기, 재생기, 응축기, 교축밸브, 터빈-펌프의 엑서지 파괴율 Dh, Dr, Dc, Dtv, Dtp와 열원 유체 및 냉각수에 의한 엑서지 손실률 Dso 및 Dco는 다음과 같이 구할 수 있다.
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
재생기, 분리기, 교축 밸브가 없는 ORC에서 식 (3)-(16)에 대응하는 식들은 Fig. 1의 두 시스템을 비교하면 쉽게 알아낼 수 있다.
본 논문에서는 KCS에서 암모니아-물 혼합물과, ORC에서 작동 유체에 대한 열역학적 상태량을 각각 문헌 20-21과 문헌 22-23의 방법을 사용하여 계산하였다.
3. 결과 및 고찰
본 연구에서 열원 유체는 1 kg/s의 공기로 가정하며 시뮬레이션을 위한 기본적인 시스템 데이터는 다음과 같다. 열원 온도 TS = 200℃, 터빈 입구 온도 TH = 185℃, 응축 온도 TL = 30℃, 냉각수 온도 TC = 15℃, 핀치포인트온도차 ΔTpp = 8℃, 사장 상태 온도 T0 = 15℃, 사장 상태 압력 P0 = 1 atm, 펌프 효율 ηp = 0.85, 터빈 효율 ηt = 0.85. 또한 암모니아 기본 질량 농도 xb는 10%, 20%, 30%, 40%, 50%, 60%를 고려한다18).
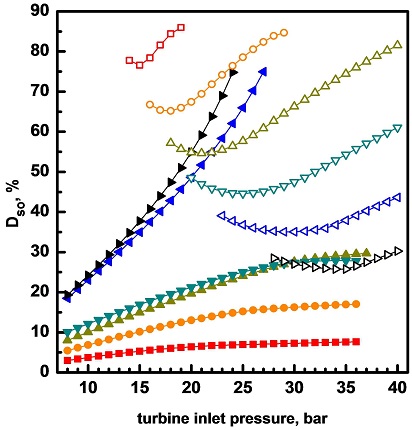
Fig. 2에서는 터빈 입구 압력, 작동 유체, 암모니아 농도의 변화가 열원 유체 배기가스의 엑서지 손실률 Dso에 미치는 영향을 보여준다. ORC에서 터빈 입구 압력이 높아지면 증발 온도가 상승하면서 결과적으로 열원 유체의 증발기 출구 온도가 높아지기 때문에 엑서지 손실률이 증가한다. 주어진 터빈 입구 압력에서는 작동 유체의 임계온도가 높아짐에 따라 엑서지 손실률이 증가해서 R601a인 경우에 가장 높고 R134a의 경우에 가장 낮다. KCS에서는 터빈 입구 압력이 증가함에 따라 엑서지 손실률이 감소하다가 최솟값에 도달한 후 다시 증가한다. 이는 다음과 같이 설명할 수 있다. 터빈 입구 압력이 증가하면 작동 유체의 증발 온도가 높아지면서 열원 유체 출구 온도를 높이는 요인이 된다. 그러나 다른 한편으로 터빈 입구 압력이 높아지면 터빈 출구 온도도 떨어지며, 이 감소 효과가 전술한 증가 요인보다 지배적이 되어 재생기를 통한 열전달이 감소하고 결과적으로 열원 유체의 출구 온도가 감소하게 된다19). 주어진 터빈 입구 압력의 경우 암모니아 농도가 증가함에 따라 엑서지 손실률이 감소하여, 엑서지 손실률은 농도가 10%인 경우에 가장 높고 농도가 60%인 경우에 가장 낮다.
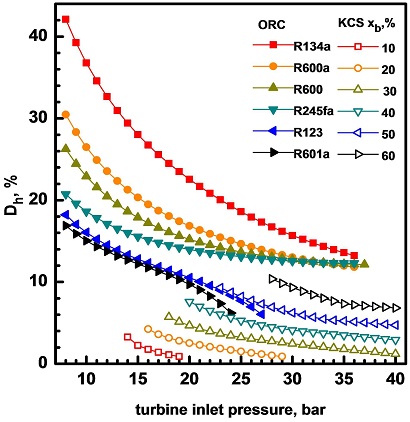
Fig. 3은 터빈 입구 압력, 작동 유체, 암모니아 농도의 변화가 증발기의 엑서지 파괴율 Dh에 미치는 영향을 보여준다. ORC에서는 터빈 입구 압력이 높을수록 엑서지 파괴율이 낮다. 이는 터빈 입구 압력이 증가하면 증발 잠열이 감소하면서 증발기의 열전달이 감소하기 때문이다. 또한 엑서지 파괴율은 작동 유체의 임계 온도가 높아짐에 따라 감소하여, R134a의 경우에 가장 높고 R601a의 경우에 가장 낮다. KCS에서는 터빈 입구 압력이 증가함에 따라 증발기의 엑서지 파괴율이 감소하며, 이는 터빈 입구 압력의 증가함에 따라 증발기의 열전달이 감소하기 때문이다. 주어진 터빈 입구 압력에서 암모니아 농도가 높아지면 증발기의 고온과 저온 유체 사이의 온도차가 확대되면서 엑서지 파괴율도 높아진다. 또한 KCS에서 증발기의 엑서지 파괴율이 ORC에 비해 훨씬 낮다는 점에 유의해야 하며, 이는 KCS의 경우에 작동 유체의 상변화가 온도가 변하면서 진행되어 엑서지 파괴가 크게 감소하는 것을 의미한다.
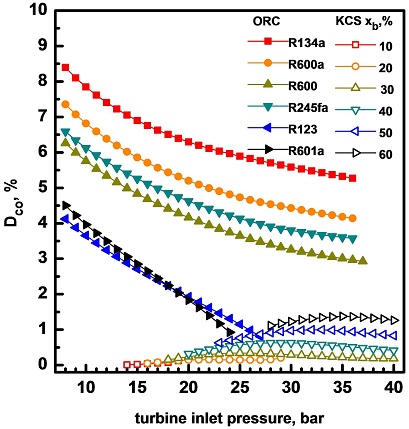
Fig. 4는 응축기 출구에서 냉각수에 의한 엑서지 손실률 Dco가 터빈 입구 압력, 작동 유체, 암모니아 농도의 변화에 따라 어떻게 변화하는지를 보여준다. ORC에서는 터빈 입구 압력이 높을수록 터빈을 통한 작동 유체의 팽창비가 증가하면서 작동 유체의 터빈 출구 온도가 떨어지기 때문에 결과적으로 엑서지 손실률이 감소한다. 주어진 터빈 입구 압력에서 엑서지 손실률은 작동 유체의 임계 온도가 높을수록 작아져서 R134a의 경우에 가장 높고 R123이나 R601a의 경우에 가장 낮다. KCS에서는 터빈 입구 압력이 높아지면 터빈 출구에서 작동 유체의 온도가 낮아지기 때문에 엑서지 손실률이 낮아지며, KCS의 엑서지 손실률은 ORC에 비해 훨씬 낮다는 것이 잘 드러난다.
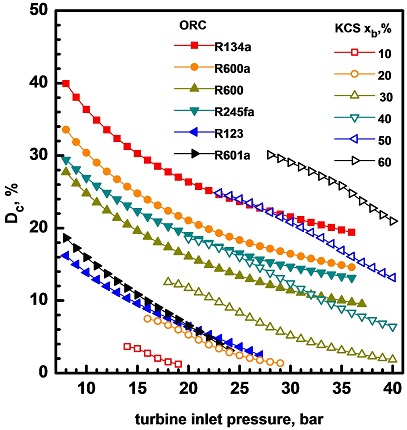
Fig. 5는 터빈 입구 압력, 작동 유체, 암모니아 농도의 변화에 따른 응축기에서의 엑서지 파괴율 Dc의 변화를 보여준다. ORC에서는 터빈 입구 압력이 높을수록 터빈 출구에서의 작동 유체의 온도가 낮아지면서 결과적으로 응축기에서 제거되는 열이 감소하므로 터빈 입구 압력이 높아지면 엑서지 파괴율이 낮아진다. 또한 작동유체의 임계 온도가 높을수록 엑서지 파괴율이 낮아져서 응축기에서의 엑서지 파괴율은 R134a의 경우에 가장 높고 R601a의 경우에 가장 낮다. KCS에서는 터빈 입구 압력이 증가함에 따라 터빈 출구에서 작동 유체의 온도가 낮아지기 때문에 응축기의 엑서지 파괴율이 감소한다. 또한 응축기의 엑서지 파괴율은 암모니아 농도가 높아질수록 높아져서 암모니아 농도가 10%일 때 가장 낮고 60%일 때 가장 높다.
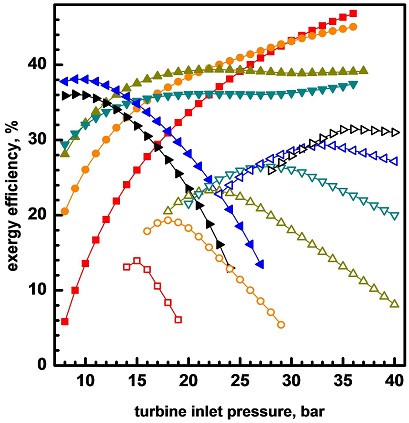
Fig. 6은 터빈 입구 압력, 작동유체, 암모니아 농도의 변화가 시스템의 엑서지 효율에 미치는 영향을 보여준다. ORC에서 터빈 입구 압력이 엑서지 효율에 미치는 영향은 작동 유체에 따라 다르다. 터빈 입구 압력이 증가함에 따라 엑서지 효율은 R134a나 R600a처럼 임계온도가 낮은 작동 유체의 경우에는 단조 증가하나, R600이나 R245fa의 경우에는 낮은 압력 범위에서는 증가하다가 압력이 높아지면 변화가 거의 없고, R123 및 R601a와 같이 임계 온도가 높은 작동 유체의 경우에는 처음에는 증가하다가 감소하여 극댓값을 갖는다. 이에 따라 터빈 입구 압력이 낮은 범위에서는 R123, 중간 범위에서는 R600과 R600a 그리고 높은 범위에서는 R134a인 경우 엑서지 효율이 가장 높은 것을 알 수 있다. KCS에서는 터빈 입구 압력이 증가함에 따라 엑서지 효율은 먼저 증가하다가 극댓값에 도달한 후 다시 감소한다. 최대 엑서지 효율과 그에 상응하는 최적의 터빈 입구 압력은 암모니아 농도가 높아짐에 따라 증가하여 암모니아 농도가 10%일 때 13.9% 및 15 bar, 20%일 때 19.3% 및 18 bar, 30%일 때 23.3% 및 22 bar, 40%일 때 26.4% 및 28 bar, 50%일 때 29.3% 및 33 bar 그리고 60%일 때 30.8% 및 34 bar가 된다. 주어진 데이터 범위에서 엑서지 최대 효율은 ORC의 경우가 KCS에 비해 높다.
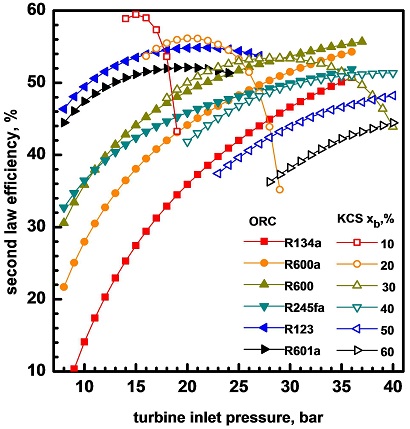
Fig. 7은 터빈 입구 압력, 작동 유체, 암모니아 농도의 변화가 2법칙 효율에 미치는 영향을 보여준다. 일반적으로 증발기를 나온 열원 유체가 추가적으로 에너지 시스템에 활용되면 2법칙 효율이 더 의미가 있으며, 그렇지 않으면 엑서지 효율이 더 의미가 있다고 할 수 있다. ORC의 2법칙 효율은 R134a, R600a, R600, R245fa와 같이 임계 온도가 상대적으로 낮은 작동 유체의 경우 터빈 입구 압력이 높아짐에 따라 단순 증가하며, R123 및 R601a와 같이 임계 온도가 상대적으로 높은 작동 유체의 경우에는 터빈 입구 압력이 변화함에 따라 극댓값을 갖는다. KCS의 2법칙 효율은 암모니아 농도가 10%에서 30%까지 낮은 경우에는 터빈 입구 압력에 대해 극댓값을 갖지만, 암모니아 농도가 40%에서 60%까지 높은 경우에는 터빈 입구 압력이 높아짐에 따라 단순 증가한다. 주어진 데이터 범위에서 2법칙 최대 효율은 KCS의 경우가 ORC에 비해 높다.
4. 결 론
본 논문에서는 현열 형태의 저등급 열원으로 구동되는 ORC와 KCS에 대한 엑서지 성능을 비교 해석하였다. ORC에서는 R134a, R600a, R600, R245fa, R123 및 R601a의 여섯 가지 물질을 작동 유체로 고려하였으며, KCS에서는 10%부터 60%까지의 암모니아 농도를 고려하였다.
주요 해석 결과는 다음과 같다. 열원 유체의 엑서지 손실률은 ORC의 경우에는 작동 유체의 임계온도가 높아질수록 증가하며, KCS에서는 암모니아 농도가 높아질수록 감소한다. 응축기 냉각수의 엑서지 손실률은 이와 반대로 ORC의 경우에는 작동유체의 임계온도가 높아질수록 감소하며 KCS에서는 암모니아 농도가 높아질수록 증가한다.
증발기에서 엑서지 파괴율은 KCS가 ORC에 비해 훨씬 낮고, ORC와 KCS 모두 터빈 입구 압력이 높아짐에 따라 감소하며, ORC의 경우에는 작동 유체의 임계 온도가 높을수록 감소하고 KCS에서는 암모니아 농도가 높을수록 증가한다.
주어진 데이터 범위에서 최대 엑서지 효율은 ORC가 KCS에 비해 높지만 최대 2법칙 효율은 KCS가 ORC에 비해 높다.
Acknowledgments
이 연구는 금오공과대학교 학술연구비로 지원되었습니다.
References
-
M. Aguirre and G. Ibikunle, “Determinants of renewable energy growth: a global sample analysis”, Energy Policy, Vol. 69, 2014, pp. 374-384.
[https://doi.org/10.1016/j.enpol.2014.02.036]

-
P. Roy, M. Désilets, N. Galanis, H. Nesreddine, and E. Cayer, “Thermodynamic analysis of a power cycle using a low-temperature source and a binary NH3–H2O mixture as working fluid”, Int. J. Therm. Sci., Vol. 49, No. 1, 2010, pp. 48-58.
[https://doi.org/10.1016/j.ijthermalsci.2009.05.014]

-
K. H. Kim, H. J. Ko, and K. Kim, “Assessment of pinch point characteristics in heat exchangers and condensers of ammonia–water based power cycles”, Applied Energy, Vol. 113, 2014, pp. 970-981.
[https://doi.org/10.1016/j.apenergy.2013.08.055]

-
A. Schuster, S. Karellas, E. Kakaras, and H. Spliethoff, “Energetic and economic investigation of organic Rankine cycle applications”, Appl. Therm. Eng., Vol. 29, No. 8-9, 2009, pp. 1809-1817.
[https://doi.org/10.1016/j.applthermaleng.2008.08.016]

-
K. H. Kim, C. H. Han, and K. Kim, “Effects of ammonia concentration on the thermodynamic performances of ammonia–water based power cycles”, Thermochimica Acta, Vol. 530, 2012, pp. 7-16.
[https://doi.org/10.1016/j.tca.2011.11.028]

-
T. C. Hung, S. K. Wang, C. H. Kuo, B. S. Pei, and K. F. Tsai, “A study of organic working fluids on system efficiency of an ORC using low-grade energy sources”, Energy, Vol. 35, No. 3, 2010, pp. 1403-1411.
[https://doi.org/10.1016/j.energy.2009.11.025]

-
K. H. Kim and H. Perez-Blanco, “Performance analysis of a combined organic Rankine cycle and vapor compression cycle for power and refrigeration cogeneration”, Appl. Therm. Eng., Vol. 91, 2015, pp. 964-974.
[https://doi.org/10.1016/j.applthermaleng.2015.04.062]

-
Y. Dai, J. Wang, and L. Gao, “Parametric optimization and comparative study of organic Rankine cycle (ORC) for low grade waste heat recovery”, Energy Convers. Manag., Vol. 50, No. 3, 2009, pp. 576-582.
[https://doi.org/10.1016/j.enconman.2008.10.018]

-
U. Drescher and D. Brüeggemann, “Fluid selection for the organic Rankine cycle (ORC) in biomass power and heat plants”, Appl. Therm. Eng., Vol. 27, No. 1, 2007, pp. 223-228.
[https://doi.org/10.1016/j.applthermaleng.2006.04.024]

-
N. A. Lai, M. Wendland, and J. Fischer, “Working fluids for high-temperature organic Rankine cycles”, Energy, Vol. 36, No. 1, 2011, pp. 199-211.
[https://doi.org/10.1016/j.energy.2010.10.051]

-
B. F. Tchanche, G. Papadakis, G. Lambrinos, and A. Frangoudakis, “Fluid selection for a low-temperature solar organic Rankine cycle”, Appl. Therm. Eng., Vol. 29, No. 11-12, 2009, pp. 2468-2476.
[https://doi.org/10.1016/j.applthermaleng.2008.12.025]

-
V. A. Prisyazhniuk, “Alternative trends in development of thermal power plants”, Appl. Therm. Eng., Vol. 28, No. 2-3, 2008, pp. 190-194.
[https://doi.org/10.1016/j.applthermaleng.2007.03.025]

-
K. H. Kim and K. C. Kim, “Thermodynamic performance analysis of a combined power cycle using low grade heat source and LNG cold energy”, Appl. Therm. Eng., Vol. 70, No. 1, 2014, pp. 50-60.
[https://doi.org/10.1016/j.applthermaleng.2014.04.064]

-
S. Ogriseck, “Integration of Kalina cycle in a combined heat and power plant, a case study”, Appl. Therm. Eng., Vol. 29, No. 14-15, 2009, pp. 2843-2848.
[https://doi.org/10.1016/j.applthermaleng.2009.02.006]

-
A. Modi and F. Haglind, “Thermodynamic optimisation and analysis of four Kalina cycle layouts for high temperature applications”, Appl. Therm. Eng., Vol. 76, 2015, pp. 196-205.
[https://doi.org/10.1016/j.applthermaleng.2014.11.047]

-
F. Sun, W. Zhou, Y. Ikegami, K. Nakagami, and X. Su, “Energy–exergy analysis and optimization of the solar-boosted Kalina cycle system 11 (KCS-11)”, Renewable Energy, Vol. 66, 2014, pp. 268-279.
[https://doi.org/10.1016/j.renene.2013.12.015]

- A. Bejan, “Advanced engineering thermodynamics”, 3rd ed, John Wiley & Sons, USA, 2006.
- K. H. Kim, Y. G. Bae, Y. G. Jung, and S. W. Kim, “Comparative performance analysis of ammonia-water Rankine cycle and Kalina cycle for recovery of low-temperature heat source”, Trans. of Korean Hydrogen and New Energy Society, Vol. 29, No. 2, 2018, pp. 148-154.
- S. W. Kim and K. H. Kim, “Comparative exergy analysis of organic and ammonia-water Rankine cycles”, Int. J. Mech. Prod. Eng., Vol. 5, No. 4, 2017, pp. 89-93. Retrieved from http://www.iraj.in/journal/journal_file/journal_pdf/2-365-149854409889-93.pdf, .
-
F. Xu and D. Y. Goswami, “Thermodynamic properties of ammonia–water mixtures for power-cycle applications”, Energy, Vol. 24, No. 6, 1999, pp. 525-536.
[https://doi.org/10.1016/S0360-5442(99)00007-9]

- J. M. Smith, H. C. Van Ness, and M. M. Abbott, “Introduction to chemical engineering thermodynamics”, 7th Ed. McGraw-Hill, USA, 2005.
-
T. Yang, G. J. Chen, and T. M. Guo, “Extension of the Wong-Sandler mixing rule to the three-parameter Patel-Teja equation of state: application up to the near-critical region”, Chem. Eng. J., Vol. 67, No. 1, 1997, pp. 27-36.
[https://doi.org/10.1016/S1385-8947(97)00012-0]

-
J. Gao, L. D. Li, Z. Y. Zhu, and S. G. Ru, “Vapor–liquid equilibria calculation for asymmetric systems using Patel–Teja equation of state with a new mixing rule”, Fluid Phase Equilibrium, Vol. 224, No. 2, 2004, pp. 213-219.
[https://doi.org/10.1016/j.fluid.2004.05.007]