반도체 칩 테스트용 챔버 형상에 따른 유동 균일성에 대한 수치적 연구

2.1 기준 챔버 형상

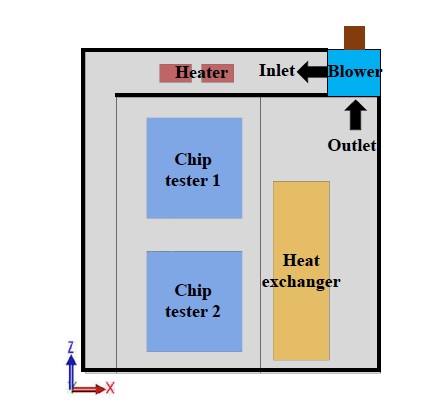
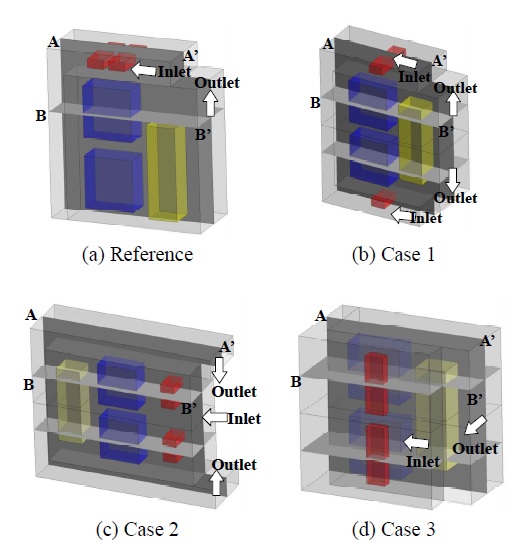
외부 형상은 직육면체 형태를 하고 있으며 내부에는 공기를 가열하는 히터(heater), 반도체 칩 검사를 위한 칩 테스터 및 공기를 냉각하는 열교환기(heat exchanger)로 구성되어 있다. 챔버 내부 유동제어를 위해 Fig. 1에서 보는 바와 같이 우측 상단에 송풍기가 설치되어 있으며, 송풍기에 의한 유동은 챔버의 입구에서 일정한 유량이 반시계방향으로 순환하여 출구로 토출되는 구조로 되어있다.

Fig. 1.

Cross-sectional view of the test chamber

2.2 수치해석 방법

본 연구에서는 챔버의 유로 변경에 따른 칩 테스터 내부의 유속 표준편차 및 유동 특성 분석을 위해 상용 유동해석 프로그램인 ANSYS CFX 19.1 (ANSYS Inc., Pennsylvania Cannonsburg, USA)⁸⁾을 이용하였다. 챔버 내부 유동영역은 삼차원 비압축성 정상상태 Reynolds-averaged Navier-Stokes (RANS) 방정식을 사용하여 유동해석을 수행하였으며, 난류모델로는 k-ε 난류 모델⁹⁾을 사용하였다.

작동유체는 25˚C의 공기를 사용하였으며, 입구의 경계조건으로는 송풍기 정격 사양의 유량이 흐르도록 9.57 m/s의 속도로 설정하였으며, 출구 경계조건은 표준 상태의 대기압으로 가정하여 부여하였다. 챔버의 벽 및 히터와 칩 테스터 1 사이에는 no-slip condition의 벽 경계조건을 부여하였다. 주요 구성품인 히터, 열교환기 및 칩 테스터는 다공성 매질(porous media)로 가정하였고, 각 구성품의 다공성질을 모사하기 위하여 손실모델을 적용하였다. 손실모델은 ANSYS CFX에서 다공성 매질로 해석하고자 하는 경우 사용하는 모델이다. 주요 구성품에 대한 주 유동방향의 손실은 2차 저항계수 손실모델을 사용하였으며, 1차 및 2차 저항계수는 주요 구성품의 압력강하 실험결과로부터 계산된 값을 적용하였다. 주 유동방향에 대한 수직방향의 손실은 횡손실 옵션에서 주 유동방향 저항계수에 대한 지수를 적용하여 계산하였다.

유동해석을 위한 삼차원 형상생성, 격자생성, 경계조건 부여, 유동해석 및 결과분석은 각각 Solidworks, ANSYS-Mesh, CFX-Pre, CFX-Solver 및 CFX-Post를 사용하였다.

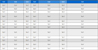
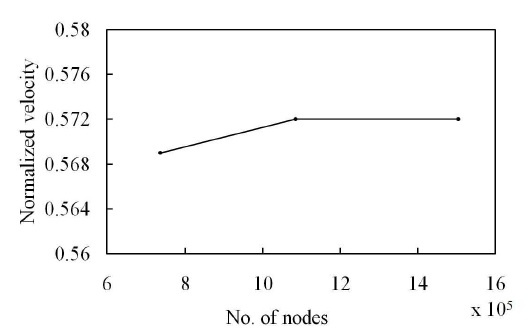
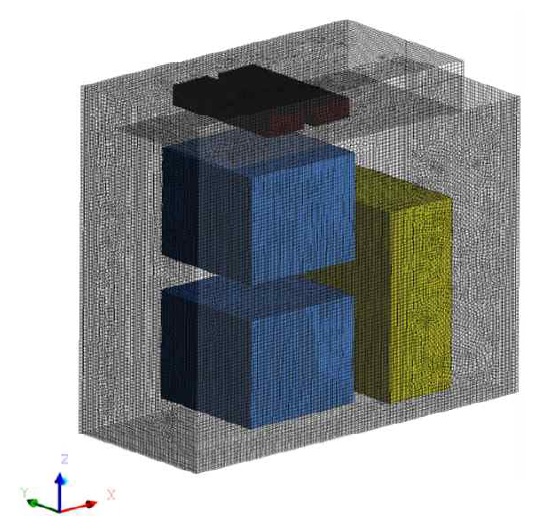
본 연구에서 구성한 계산영역의 격자 의존성을 제거하기 위해 Roache¹⁰⁾, Celik과 Karatekin¹¹⁾에 의해 제안된 방법에 따라 격자 의존성 시험을 진행하였다. 이 방법은 Richardson 외삽법(extrapolation)을 기반으로 이산화 오류를 예측하여 수치해석의 불확실성을 지표로 나타내는 grid convergence index (GCI)를 분석하는 과정이다. 이를 위해 서로 다른 3개의 격자계(N₁, N₂ 및 N₃)를 구성하였고, 격자 세분화 인자(grid refinement factor, r)를 1.3으로 설정한 격자 의존성 시험 결과를 Table 1에 나타내었다. 이산화 오류를 비교하기 위해 칩 테스터 내부의 평균속도(V_c)를 사용하였으며, 송풍기 정격유량의 속도로 무차원화한 속도(V_cn)가 비교되었다. 격자수가 증가할수록 칩 테스터 내부의 평균 유속이 점차 수렴하는 경향을 보이고 있으며, N₁을 사용한 경우 외삽 상대 오차(e_ext²¹)는 0.00138%, GCI_fine²¹은 0.00172%로 매우 작은 수치적 불확실성이 확인되었다. 따라서 Richardson 외삽법을 기반으로 최적 격자계를 N₁으로 선정하였고, Fig. 2와 같이 격자수에 따른 칩 테스터 내부 평균유속을 도식화하였다. Fig. 2에 나타난 바와 같이 격자수가 증가할수록 칩 테스터 내부의 유동속도가 수렴하는 경향을 보이고 있으며, 약 150만 개의 격자수를 사용한 N₁의 격자계를 Fig. 3에 나타내었다.

Table 1.

Grid convergence index for the grid dependency test

Fig. 2.

Result of the grid dependency test

Fig. 3.

Grid system of the reference chamber

2.3 챔버 주요 부품 성능시험

반도체 챔버의 주요 구성품은 실제형상이 매우 복잡하기 때문에 원형 모델을 직접 모사하여 계산하면 많은 수의 격자가 필요하며 높은 계산비용 때문에 유동해석이 매우 어렵거나 불가능한 경우가 많다. 따라서 각 구성품의 형상을 단순화하여 다공성 매질로 가정하여 유동해석을 수행하였다. Jeong과 Lee¹²⁾ 및 Jung 등¹³⁾은 다공성 매질로 대체하는 모델링 기법의 유효성을 확인하기 위하여 원형모델과 다공성 모델을 선정하여 유동해석을 진행하였으며, 유동해석 결과 차이는 미비하고 전반적인 경향은 일치함을 확인하였다. 다공성 매질로 모사하기 위하여 각 구성품에 대한 손실모델을 도출하였다. 이를 위해 챔버를 구성하는 각 구성품의 시스템 저항곡선을 Fig. 4와 같이 실험을 통해 도출하였다. 각 구성품에 대한 속도에 따른 손실계수는 식 (1)의 손실법칙(Darcy’s Law)¹⁴⁾을 이용하여 구하였으며, 각 부품에 대한 계수값은 Table 2에 나타내었다.

Fig. 4.

Experimental set up for investigating the system loss

Table 2.

Coefficients of Darcy’s Law for chamber components

여기서 P, x 및 V는 각각 정압력, 측정 기준점으로부터의 거리 및 유동속도를 의미한다.

2.4 챔버 형상 사례 연구

본 연구에서 사용된 챔버 형상은 Fig. 5의 Cases 1-3과 같다. 칩 테스터는 기준 챔버 형상과 같이 2단으로 유지하였으며, 히터와 열교환기의 위치는 챔버의 입구와 출구의 위치에 따라 변경하였다. Case 1의 경우 챔버의 입구와 출구 위치를 각각 위·아래로 한 쌍으로 위치하며, 기존 송풍기의 절반 용량인 송풍기2대가 각각 상단과 하단에 위치한다. 열교환기는 기준 모델과 같은 위치로 구성하였고, 히터는 상단과 하단에 각각 1개씩 위치하고 있다. Case 2의 경우 히터를 통해 가열된 공기가 칩 테스터로 직접적으로 유입될 수 있도록 송풍기를 위치시켰고, 열교환기의 경우 기존 열교환기의 열교환 면적을 반으로 줄여 상단과 하단부에 각각 위치시켰다. Case 3은 각 구성품의 위치가 기준 챔버 모델과 동일하게 설정하였고, 유동 방향이 옆으로 더 넓은 면적으로 진행하도록 송풍기를 위치시켰다.

Fig. 5.

Three-dimensional geometry of the test chamber

3.1 챔버 내부 유동특성 분석

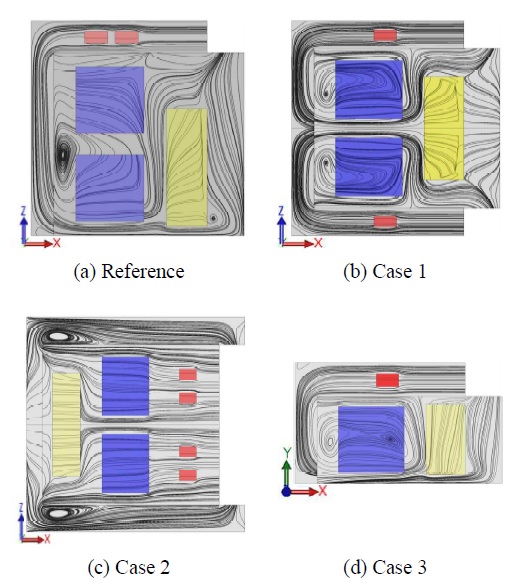
챔버 내부 3차원 유동을 Fig. 6에 나타내었다. 기준 챔버 형상의 경우, Fig. 6(a) (Fig. 5[a] 내 A-A` 단면)에서 보는 바와 같이 유선이 칩 테스터 2 아래에 상대적으로 많이 분포하고 있는 것을 알 수 있다. 즉, 송풍기로부터 유입된 유동이 챔버의 벽면을 따라 진행하여 챔버의 출구부로 토출되고 있고, 칩 테스터 1 내부로의 공기 유입은 송풍기로부터 직접 유입되지 않고 칩 테스터 2를 통과한 공기가 유입됨이 관찰되었다.

Fig. 6.

Comparison of the streamline distribution

Case 1 (Fig. 5[b] 내 A-A` 단면)은 상단부와 하단부에 위치한 각각의 송풍기로부터 공기가 유입되어 유동이 칩 테스터를 기준으로 대칭적으로 분포하고 있다. 즉, 상단과 하단 송풍기로부터 유입되는 공기는 각각 반시계방향과 시계방향으로 토출된다. 이러한 유동특성으로 인해 칩 테스터 1의 하단과 칩 테스터 2의 상단으로 유동이 많이 유입되며, 칩 테스터 1의 상단과 칩 테스터 2의 하단의 경우 송풍기로부터 직접적으로 유입되지 않는 것이 관찰되었다.

Case 2는 Fig. 6(c) (Fig. 5[c] 내 A-A` 단면)에서 보는 바와 같이 송풍기로부터 유입되는 공기가 칩 테스터 내부로 직접 통과하여 상단과 하단에 위치한 챔버의 출구로 토출되는 것을 알 수 있다. 또한, 칩 테스터 전체 층으로 송풍기 유동이 고르게 유입되는 것을 관찰하였다.

Fig. 6(d) (Fig. 5[d] 내 B-B` 단면)에 나타낸 Case 3의 경우 기준 챔버 형상과 같이 챔버의 벽면을 따라 진행한 유동이 칩 테스터 하단부로 유입되고, 다시 칩 테스터 상단부로 재순환되는 유동 특성이 관찰되었다.

3.2 칩 테스터 내부 유동 균일성 분석

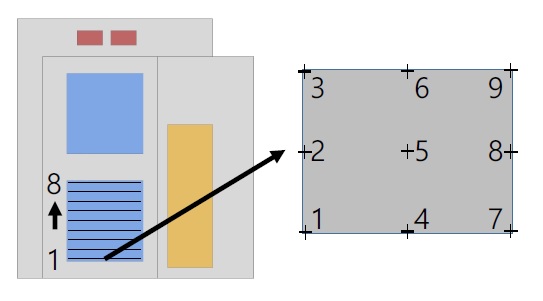
앞서 살펴본 바와 같이 유동해석을 통해 챔버 형상 사례 연구를 수행하였으며, 각 구성품의 위치 변화에 따라서 챔버 내부의 유동특성에 상당한 영향을 미치는 것이 확인되었다. 아울러, 이러한 유동특성 변화로 인해서 칩 테스터 내부로 유입되는 유량 및 균일성도 영향을 받는 것을 알 수 있었다. 따라서, 칩 테스터 내부의 유속 분포를 정량적으로 분석하기 위해 Fig. 7과 같이 칩 테스터 내부에 수직방향으로 일정한 간격의 8개의 층을 생성하였으며, 각 층에서 동일한 간격으로 9개의 점을 찍어 속도를 측정하였다. 각 지점에서 측정한 속도는 송풍기의 유입 속도인 9.57 m/s로 나누어 무차원화 하였으며, 칩 테스터 1과 칩 테스터 2 내부의 평균유속을 비교하였다. 기준 챔버 모델은 칩 테스터 1 내부의 무차원화 된 평균유속이 1.43으로 예측되었고, 칩 테스터 2는 0.57로 예측되었다. 각 구성품의 위치를 변경한 챔버 모델인 Case 1, 2 및 3의 경우 송풍기의 유동방향으로 칩 테스터가 대칭으로 배치되어 있기 때문에 각 칩 테스터에서의 평균 유속이 다음과 같이 동일하게 예측되었다. Case 1의 경우 0.56, Case 2의 경우 0.45 그리고 Case 3의 경우 0.96으로 예측되었다. 변경 챔버 모델의 경우 기준 챔버 모델과 비교하여 칩 테스터 간의 평균유속의 차이가 없고, 동일하였다.

Fig. 7.

Location of comparison planes and points for measuring the velocity

챔버 내부의 속도 분포를 가시화하여 비교하기 위해 Fig. 5에 나타낸 각 단면에서 무차원화된 속도 분포를 Fig. 8에 나타내었다.

Fig. 8.

Comparison of the velocity distribution

기준 챔버 형상의 경우, Fig. 8(a)에서 보는 바와 같이 칩 테스터 2 하단부에서 상대적으로 빠른 속도분포가 관찰되었다. 칩 테스터 1 내부에는 속도가 0.4 이하로 분포하였고, 칩 테스터 2보다 내부 유속이 상대적으로 낮게 형성되었다. 이는 송풍기로부터 유입된 공기가 상대적으로 저항이 적은 챔버의 벽면과 바닥면을 따라 진행하여 출구부로 토출되므로 칩 테스터 2의 하단부에서 빠른 속도가 관찰된 것으로 볼 수 있다.

Case 1은 상단부와 하단부에 위치한 각각의 송풍기로부터 공기가 유입되어 칩 테스터를 기준으로 대칭적으로 흐른다. 이러한 유동특성으로 인해 칩 테스터 1의 하단과 칩 테스터 2의 상단에 상대적으로 속도가 높게 형성되는 것을 확인할 수 있으며, 칩 테스터 1의 상단과 칩 테스터 2의 하단의 경우 상대적으로 낮은 속도가 관찰되었다.

Case 2는 송풍기로부터 유입되는 공기가 칩 테스터 내부로 직접 통과하기 때문에 칩 테스터 내부의 공기속도는 0.3 이하로 일정하게 분포하고 있었으며, Fig. 6에서 확인한 바와 같이 칩 테스터 내부에서 유동이 재순환되지 않기 때문에 유속의 균일성이 우수할 것으로 사료된다.

Case 3의 경우 기준 챔버 형상과 유사하게 공기가 챔버의 벽면과 바닥면을 따라 진행하였고, 칩 테스터 하단부에 상대적으로 많은 공기가 유입되었다. 그러나 기준 형상과 다르게 칩 테스터가 평행하게 배치되어 있어서 칩 테스터 1과 2의 내부 유속분포는 동일한 것으로 예측되었다.

칩 테스터 내부 유동 균일성을 보다 정량적으로 비교하기 위해 Fig. 7에 표기한 각 층마다 9개의 점에서 속도를 측정하여 표준편차를 비교하였다. 표준편차는 식 (2)를 사용하여 계산하였고, 정의는 다음과 같다.

여기서 S는 표본의 표본표준편차, $$ \stackrel{-}{y}$$는 표본평균을 나타낸다.

칩 테스터 1과 칩 테스터 2의 각 층마다 계산된 표준편차를 Table 3에 나타냈으며, 이를 통해 각 층의 유속분포의 균일도를 확인할 수 있었다. Case 2는 다른 챔버 모델 보다 모든 층에서 균일한 유속분포를 나타냈으며, 이러한 결과는 송풍기로부터 유입되는 공기가 칩 테스터 내부로 직접 통과하여 칩 테스터 전체 층으로 유동이 고르게 유입됐기 때문이다. 그리고 공기가 챔버의 벽면과 바닥면을 따라 진행하고, 칩 테스터 하단부에 상대적으로 많은 공기가 유입되는 Case 3은 모든 층에서 불균일한 유속분포를 나타내었다. 기준 챔버 모델과 Case 2는 상대적으로 공기가 많이 유입되는 층에서 유속분포가 불균일하였으며, 공기가 적게 유입되는 층에서는 상대적으로 유속분포가 균일하였다.

Table 3.

Standard deviation of the comparison planes

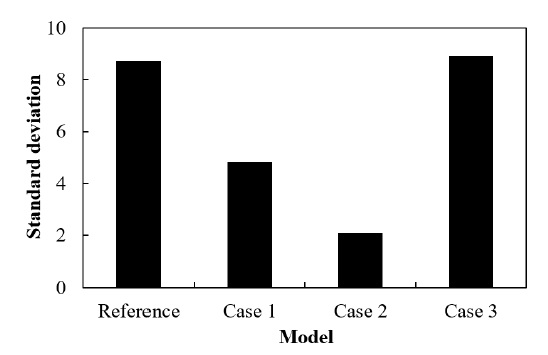
Fig. 9는 각 챔버 모델의 칩 테스터 전체에 대한 총 144개 점에서 속도를 측정하여 계산된 표준편차를 나타낸 그림이다. 기존 챔버 모델의 경우 8.73의 표준편차를 나타낸 반면, Cases 1-3의 표준편차는 각각 4.83, 2.10 및 8.93을 나타내었다. 결과적으로 Case 2의 표준편차가 가장 작았으며, 기존 챔버 모델과 비교하여 유동 균일성이 약 4배 정도 향상되었다. 칩 테스터 내부의 유속분포는 Case 2일 때 가장 균일함을 Table 3과 Fig. 9를 통해 정량적으로 확인하였다.

Fig. 9.

Comparison of the standard deviation in the chip testers