액화 수소 저장 조건에서 오르토-파라 수소 평형 분석
2025 The Korean Hydrogen and New Energy Society. All rights reserved.
Abstract
Due to its significantly higher storage density compared to gaseous hydrogen, liquefied hydrogen is gaining attention as a key storage method for hydrogen infrastructure, including hydrogen refueling stations. However, the ortho-to-para hydrogen conversion process generates heat, which can lead to vaporization of the liquid hydrogen. Therefore, the transition must be carefully considered in any safety analysis of liquefied hydrogen storage systems. The present study develops a thermodynamic equilibrium model to analyze the ortho-para hydrogen conversion behavior under liquefied hydrogen storage conditions. By considering chemical and phase equilibria between isomers, the model predicts equilibrium composition, temperature, pressure, and phase distribution. Simulation results reveal that insufficient catalytic conversion to para-hydrogen can lead to significant pressure rise due to exothermic ortho-para transition, potentially exceeding critical limits. The findings highlight the necessity of maximizing para-hydrogen content during liquefaction for safe storage, especially under isochoric and cryogenic conditions.
Keywords:
Liquefied hydrogen, Hydrogen storage, Ortho-hydrogen, Para-hydrogen, Hydrogen equilibrium키워드:
액화 수소, 수소 저장, 오르토 수소, 파라 수소, 수소 평형1. 서 론
에너지는 인류가 유지되기 위한 필수적인 자원이며 화석연료는 산업혁명 이후 급속한 경제 발전을 가능하게 해준 에너지원으로서 오랜 기간 동안 중요한 역할을 담당해 왔다. 에너지 자원으로서 안정적인 확보와 사용의 편의성과 함께 인류가 장기간 화석연료에 의존하게 된 주요 원인 중 하나는 화석연료 사용에 의한 환경 파괴가 인식하지 못할 수준으로 느리게 진행되었기 때문이다. 그러나 지난 3세기 동안 화석연료 사용으로 배출된 온실가스에 의한 기후 변화 문제는 더 이상 외면할 수 없는 수준에 도달하였다.
화석연료에 대한 의존성을 낮추는 동시에 지속 가능한 에너지 시스템을 구축하는 것은 전 지구적인 에너지 전환 흐름 속에서 가장 시급한 과제로 대두되고 있다. 현재 추세대로라면 2050년까지 지구 평균 온도는 산업화 이전 대비 3-6℃ 상승할 것으로 전망되며1) 이는 생태계, 사회, 경제 전반에 걸쳐 치명적인 영향을 미칠 것으로 예측된다. 이러한 배경 속에서 수소는 탄소중립(net-zero emissions, NZE)을 달성하기 위한 핵심 에너지원으로 부상하고 있다2-4).
수소는 가장 가벼운 원소로 연소 시 수증기만 배출하는 청정에너지 매체이다. 태양광, 풍력 등 다양한 재생에너지를 활용한 생산이 가능하기 때문에 재생에너지의 간헐성을 보완할 수 있는 에너지 저장 수단으로서 전력망 안정성에도 기여할 수 있다5,6).
활용 측면에서 이산화탄소 발생이 많은 운송 분야에서 수소 연료전지 차량(fuel cell electric vehicle, FCEV)은 기존 내연기관 차량보다 2-3배 높은 효율을 갖고 있으며 장거리 주행과 빠른 충전이 가능하다는 장점이 있다. 따라서 제철, 화학과 같은 전기화가 어려운 산업, 장거리 운송, 항공, 해운 등에서의 탈탄소화 수단으로 수소가 주목받고 있다1).
수소는 단위 질량당 에너지 밀도가 약 120 MJ/kg으로 매우 높아 미래 청정에너지의 핵심 자원으로 주목받고 있다7). 그러나 수소는 상온, 상압에서의 밀도(0.0899 kg/m3)가 매우 낮아 실질적인 활용을 위해서는 고밀도 저장 기술이 필수적이다. 특히 운송용 연료로 활용하기 위해서는 한 번 충전으로 장거리 주행이 가능한 수준의 저장 밀도가 요구되며 이는 기존 내연기관 차량과의 경쟁력을 확보하기 위한 핵심 조건 중 하나이다8). 현재 상용화된 고압(350-700 bar) 기체 저장은 비교적 기술 성숙도가 높지만 중량 대비 저장 효율이 낮고 압축 과정에서 수소 에너지의 약 13-18%가 소비되는 단점이 있다7). 이에 따라 저장 효율을 높이기 위한 액체 수소 저장(-253℃) 또는 금속 수소화물과 같은 고체 저장 방식이 대안으로 제시되고 있으며 이들 방식은 부피 대비 수소 저장 밀도가 높은 것이 특징이다9). 이러한 고밀도 저장의 필요성은 에너지 인프라 및 모빌리티 분야 전반에 걸쳐 더욱 강조되고 있다.
액체 수소 저장 방식은 동일한 부피 내에서 약 70.8 kg/m3의 밀도를 구현하여 저장 효율은 우수하지만 액화 공정에서 수소 에너지의 약 30-40%가 손실되고 상온 노출에 따른 boil-off 현상도 해결 과제로 남아 있다7,9). 한편 고체 수소 저장체(MgH2, NaBH4 등)는 안정적인 상온 저장이 가능하다는 장점이 있으나 수소 방출 온도가 높고 반응 속도 제어가 어려워 아직까지 실용화에 제약이 따른다8,10). 따라서 다양한 저장 기술의 병용과 기술 간 통합 설계가 향후 수소 경제 실현을 위한 관건이 될 것이다.
최근에는 액체 수소를 이용하는 수소 인프라 구축 확대가 활발히 진행되고 있다. 액체 수소 저장은 높은 에너지 밀도 덕분에 고출력과 장거리 운송이 요구되는 분야, 예컨대 고속철, 선박, 항공기 등에 적합한 저장 방식으로 주목받고 있다. 이는 동일한 저장 공간 대비 기체 수소보다 약 850배 높은 저장 밀도를 제공하며 고압 기체 저장(최대 70 MPa)보다도 공간 효율성이 뛰어나기 때문이다11). 특히 액체 수소는 연료전지나 가스터빈 시스템에서 바로 기체 수소로 증발시켜 사용할 수 있기 때문에 전환 효율이 우수하며 낮은 중량으로 인하여 차량의 적재 중량 증가와 항속거리 확장에도 기여한다12). 열손실을 줄이기 위한 고진공 다층 단열(multilayer insulation, MLI) 및 스프레이형 발포 단열재(spray on foam insulation, SOFI)의 기술 발전은 저장 안정성과 장기 보존 가능성을 개선하고 있으며 기화 손실(boil-off gas, BOG) 최소화를 위한 진공 단열 시스템 및 증기 냉각 차폐 기술(vapor cooled shield, VCS) 역시 고도화되고 있다11). 따라서 액체 수소 저장은 이동성과 에너지 밀도를 동시에 요구하는 미래 수소 모빌리티의 핵심 기술로 간주된다.
두 개의 수소 원자가 결합되었기 때문에 수소 분자는 두 개의 양성자로 구성되어 있으며 이들의 핵스핀 배열에 따라 두 가지 이성질체인 오르토-수소(ortho-hydrogen, o-H2)와 파라-수소(para-hydrogen, p-H2) 로 존재한다. o-H2는 두 양성자의 핵스핀이 평행하게 정렬된 상태이고 p-H2는 두 양성자의 핵스핀이 반평행하게 정렬된 상태로 존재한다(Fig. 1).
온도에 따라 o-H2와 p-H2의 비율이 달라지며 상온에서는 약 75%의 o-H2와 25%의 p-H2가 존재한다. 상온에서 이러한 비율로 존재하는 수소를 정상 수소(normal hydrogen, n-H2)라 한다. 그러나 낮은 온도에서는 p-H2가 더 안정한 형태이므로(Fig. 1) 액화 수소 저장 시 o-H2가 p-H2로 전환되면서 발열 반응이 발생하게 된다.
o-H2에서 p-H2로의 전환은 자연적으로는 매우 느리지만 증발 엔탈피와 유사한 수준의 엔탈피 변화가 동반되는 강한 발열 반응이라는 점에서 열역학적으로 중요한 특성을 가진다12). 이러한 전환은 액화 수소 저장 과정에서 중요한 고려 사항으로 전환 과정에서 발생하는 열은 액화 수소의 일부를 기화시킬 수 있으므로 저장 효율을 높이기 위해서는 촉매를 사용하여 o-H2를 p-H2로 전환하는 과정이 필요하다13).
수소 액화 공정에서 오르토-파라 전환은 냉각 단계에서 촉매 반응을 통해 촉진된다. 촉매는 열교환기의 수소 유로 측면에 분포될 수 있으며 수소가 촉매와 완전한 접촉을 유지하는 연속적인 흐름 속에서 안정화된다. 그러나 수소 액화 공정에서 촉매를 거쳐 p-H2의 조성을 높이더라도 전환율은 평형 조성에 못 미치는 95-98%로14,15) 여전히 일부 존재하는 o-H2의 자발적인 p-H2로의 전환이 발생할 가능성이 있다.
기존 연구들13,14)은 수소의 전환 과정에 대한 기초 연구로 촉매 성능에 관심을 두고 있어 실제 상업적 액화 공정 이후 평형에 도달하지 않은 o-H2와 p-H2 사이의 전환에는 크게 관심을 두고 있지 않다.
수소의 활용 측면에서는 비평형 상태에서 평형 상태로의 전환이 액화 수소의 질적 가치를 평가하기 위해 요구된다. 액화 공정을 통해 생산된 액체 수소는 평형 조성에 있지 않기 때문에 저장 탱크 내에서 전환 반응이 발생하게 된다. 이러한 o-H2와 p-H2의 전환 특성은 수소의 저장 및 활용에 중요한 영향을 미치며 특히 액화 수소 저장 시스템의 설계 및 운용에 있어서 핵심적인 요소이다.
본 연구에서는 이전 연구들과는 달리 액화 수소의 초기 p-H2 조성에 따라 평형에 도달하였을 때 저장 탱크에서 고려해야 할 안전성의 범위를 제시하고자 하였다. 이를 위하여 두 종류의 수소 각각에 대한 기-액 상평형과 두 수소 사이의 화학반응 평형에 기초한 모델을 개발하였다. 이를 바탕으로 초기 p-H2 조성, 초기 온도, 초기 액상의 비율에 따른 평형 상태 거동을 예측하였다.
2. 수소 이성질체 전환 평형 모델
2.1 수지식
액화 수소 저장 탱크가 완전한 단열 성능을 구현하고 있어 저장 탱크에 수소가 충전된 후 추가적인 유출입이 없다면 저장 탱크를 대상으로 하는 계는 고립계(isolated system)가 된다.
수소 분자의 두 이성질체인 p-H2와 o-H2를 서로 다른 화학종으로 간주하고 두 화학종 사이의 전환을 화학 반응으로 취급한다면 액화 수소 저장 탱크는 이성분계 반응 평형 및 상평형 해석으로 해석할 수 있기 때문에 이러한 평형 모델을 개발할 수 있다.
초기에는 기상과 액상에 각각 두 종류의 수소가 존재하므로 초기 총 몰수()는 다음과 같다.
| (1) |
위 식에서 아래첨자 p와 o는 각각 p-H2와 o-H2를 의미하고 위첨자 v와 l은 각각 기상과 액상을 나타낸다. 고립계에서는 물질의 유출입이 없으므로 평형 상태에 도달하였을 때에도 총 몰수는 다음과 같이 유지된다.
| (2) |
아래첨자 e는 고립계가 최종적으로 도달하게 되는 평형 상태를 의미한다.
고립계에서는 총 내부에너지(Ut) 변화가 없기 때문에 열역학 제1법칙에 의하여 에너지 수지 또한 물질 수지와 유사하게 표현된다.
| (3) |
| (4) |
이와 함께 저장 탱크에 한정된 공간에 의한 제약으로 인하여 계의 경계가 고정되어 있는 고립계의 특성으로 전체 부피(Vt) 역시 일정한 제한 조건으로 모델에 포함된다.
| (5) |
| (6) |
초기 또는 평형 상태에서 정량적인 크기 특성인 내부에너지와 부피는 다음과 같이 단위 몰당 값인 비내부에너지(u)와 밀도(ρ)를 이용하여 계산될 수 있다.
| (7) |
| (8) |
위 식에서 i(= o,p)는 화학종을, j(= v,l)는 상을 의미하며 이후 수식들에서도 동일한 의미로 사용된다.
본 모델에서는 식 (2), (4), (6)을 각각 모델 계산의 경계 조건들을 나타내는 물질, 에너지, 부피 수지식으로 사용하였다.
2.2 평형 관계식
수소 이성질체를 다른 두 화학종으로 간주하고 이들 상호 간의 전환을 화학 반응으로 취급하면 화학 반응 평형상수 개념을 이용하여 o-H2와 p-H2의 평형 상태를 계산할 수 있다.
온도에 따른 o-H2에 대한 p-H2의 비율은 Harkness와 Deming16)이 제안한 다음과 같은 무한 급수식을 이용하여 얻을 수 있다.
| (9) |
위 식에서 x=h2/8π2JkT이고 본 연구에서는 식 (9)와 같이 분자는 4개의 항, 분모는 3개의 항까지 고려한 식을 사용하였으며 문헌에서 제시된 값들을 참고하여 cgs 단위계로 플랑크 상수 h=6.547 × 10-27, 볼츠만 상수 k=1.371 × 10-16, 수소 분자의 관성 모멘트 J=0.466 × 10-40을 이용하였다. 정확한 볼츠만 상수 값 k=1.381 × 10-16이나 본 연구에서는 다른 물성들을 포함한 모든 수치들을 문헌에서 제시한 값을 이용하기 위하여 k=1.371 × 10-16를 사용하였다.
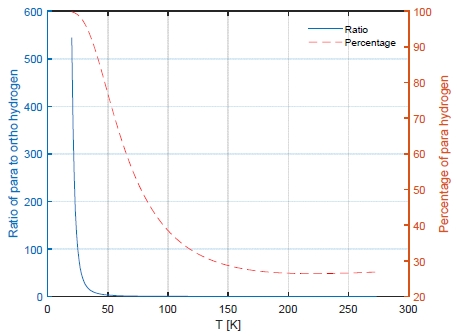
온도에 따른 평형 수소(equilibrium hydrogen, e-H2)의 조성은 p-H2를 기준으로 Fig. 2에 도시되었다. 수소의 정상 끓는점(normal boiling point) 근처인 20 K에서는 p-H2의 조성은 약 99.8%이고 온도가 증가함에 따라 n-H2에서 p-H2의 조성인 25%에 수렴하는 거동을 잘 모사하고 있다.
수소의 두 이성질체는 분자의 구조와 크기가 동일하기 때문에 이성분계 액체 상태에서 이상 용액을 가정할 수 있으며 기상 또한 이상 기체 상태에서 크게 벗어나지 않는 것으로 가정하여 기-액 평형 관계에 대해서는 Raoult의 법칙을 이용하였다.
| (10) |
여기에서 yi, xi는 각각 기상과 액상에서의 평형 조성이고 는 성분 i의 증기압을 나타낸다.
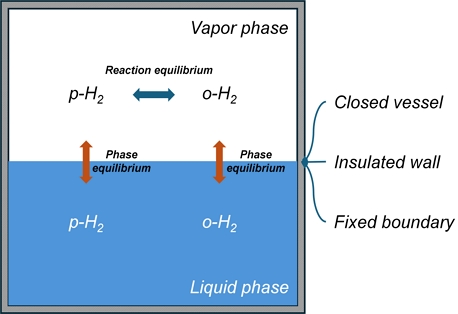
Fig. 3에는 본 모델의 평형 모델 개념을 도시하였다. 액상에서 o-H2와 p-H2의 평형 조성은 수식으로 알려져 있지 않으며 Fig. 3에서와 같이 각 화학종의 상평형과 기상에서의 두 화학종 간의 반응 평형 상태에서는 액상에서도 평형 상태로 존재하게 되므로 별도의 관계식이 필요하지 않게 된다.
2.3 수소 열역학 물성
개발된 모델을 사용하기 위해서는 수소의 열역학적 물성이 필요하다. 본 연구에서는 고립계에 대한 모델을 수립하였기 때문에 식 (7)의 비내부에너지, 식 (8)의 밀도에 대한 물성들과 함께 식 (10)에서 요구되는 증기압이 수소의 물성으로 사용된다.
일반적으로 순수한 물질의 물성은 두 열역학적 상태 변수에 의해 결정되지만 액화 수소 저장 탱크에서 기-액 평형을 유지한다면 포화 상태이기 때문에 물성들은 온도만의 함수가 된다.
포화 상태 수소 물성은 대부분 n-H2, p-H2 또는 e-H2에 대한 자료17,18)이며 o-H2에 대한 자료는 찾기 어렵다. 이는 실험적으로 순수한 o-H2를 얻을 수 없기 때문으로 판단된다. 온도가 상승하면 Fig. 2에서 보인 것과 같이 o-H2의 비율이 증가하지만 n-H2로 알려진 25% p-H2와 75%의 o-H2의 혼합물 조성에 다다르면 더 이상 온도 상승에 따른 조성의 변화를 얻을 수 없게 된다. 따라서 순수한 o-H2의 물성 데이터는 측정할 수 없게 된다. 하지만 다양한 물질의 물성 데이터들을 보유하고 있는 NIST의 데이터베이스19)에서는 o-H2의 물성을 p-H2 또는 n-H2와 구분하여 제공하고 있다. 추정컨데 p-H2와 혼합물인 n-H2로부터 o-H2 물성치를 수치적으로 계산하여 제시하는 것으로 판단된다.
본 연구에서는 순수한 o-H2의 물성이 필요하기 때문에 데이터들의 일관성을 유지하기 위하여 실험 데이터가 존재하는 p-H2에 대해서도 NIST 데이터베이스18)를 이용하였다.
데이터 범위는 기액 상평형이 존재할 수 있는 정상 끓는점부터 임계점까지로 하였으며 온도 범위 내에서 0.5 K 간격으로 데이터를 추출하였다. 데이터 범위는 Table 1에 정리되었다.
모델 계산에서는 물성들이 수식으로 표현되는 것이 편리하므로 추출된 데이터들은 적절한 상관관계식으로 회귀분석되었다.
증기압은 기화열과 열역학적으로 관계되기 때문에 열역학 이론에 기초하여 제시된다. 수소에 대해서는 복잡한 형식의 수식이 제안20)되기도 하였으나 본 연구에서는 온도와 증기압의 관계를 나타내는 일반적인 형식인 식 (11)을 이용하여 데이터로부터 수식의 계수들을 결정하였다.
| (11) |
위 식에서 증기압()과 온도(T)의 단위는 각각 bar와 K이다. 두 종류의 수소에 대해 결정된 상관관계식 계수들은 Table 2에 제시되었다.
증기압 상관관계식의 정확도는 정성적으로 Fig. 4와 Fig. 5에 각각 p-H2와 o-H2에 대해 나타내었다. 주어진 온도 범위에서 두 식 모두 정확하게 실제 데이터를 모사하고 있다.
상관관계식의 정량적 정확도는 식 (12)로 정의되는 평균 절대 비율 오차(mean absolute percentage error, MAPE)로 판단하였으며 p-H2와 o-H2에 대해 계산된 값들은 각각 0.0297%와 0.0256%로 온도 범위 내에서 증기압을 정확하게 재현하고 있는 것으로 분석되었다.
| (12) |
여기에서 ndat는 사용된 데이터의 수이며 M은 임의의 열역학 물성을 의미한다. 위첨자 dat와 cal은 각각 데이터와 계산치를 나타낸다.
밀도와 비내부에너지는 계산의 편의성을 위하여 다음과 같이 다항식으로 표현된 상관관계식을 사용하였다.
| (13) |
식 (13)에서 온도는 K 단위이며 밀도와 비내부에너지는 각각 mol/L와 kJ/mol의 단위를 갖는다.
본 연구에서는 각 물성에 대해 식 (13)의 ak를 NIST 데이터를 이용하여 회귀분석을 통해 결정하였다. 밀도와 비내부에너지에 대한 ak 값과 식 (12)로 계산된 MAPE는 각각 Table 3과 Table 4에 정리되었다.
Table 3과 Table 4에서 보인 것과 같이 식 (13)으로 밀도와 비내부에너지를 회귀분석한 결과는 만족할 만한 정확도를 보이는 것으로 확인되었다. 정성적 거동 비교는 각각 Fig. 6과 Fig. 7에 제시되었다.
3. 액체 수소 저장 평형 모사
3.1 초기 탱크 저장 조건
모델 계산을 위해 초기 조건은 p-H2와 o-H2가 평형 상태에 있는 기상에 액상 수소를 충전하는 과정을 염두에 두고 설정하였다. 시뮬레이션 조건은 온도, 초기 액상 부피 비율, 초기 액체 내 p-H2와 o-H2의 공존 비율에 따라 변경하였다. 온도 조건은 두 수소가 모두 기-액 평형을 나타낼 수 있는 범위에서 영향을 비교하기 위하여 결정하였으며 초기 액상 부피 비율은 저장 탱크 내 액체 수소 충전 최대 비율을 95%로 제한하여 다양한 조건을 설정하였다. 초기 액체 내 p-H2 비율은 급속한 액화로 인한 상평형 미도달 조건으로 n-H2에서 p-H2의 비율인 25%에서 액화 과정에서 촉매를 사용한 95%까지를 범위로 하여 조건들에 따른 영향을 평가하였다. 본 연구에서 고려한 초기 탱크 저장 조건은 Table 5와 같다.
액체의 밀도와 내부 에너지는 압력에 의존성이 낮기 때문에 저장 탱크의 초기 압력은 식 (14)와 같이 초기 온도(T0)에서 두 수소 증기압의 산술 평균으로 가정하였다.
| (14) |
3.2 평형 수소 조성 및 온도 압력 계산 알고리즘
본 모델에서는 6개의 변수(, , , , T, P)를 계산함으로써 평형을 결정하게 된다. 이를 위하여 식 (2), (7), (8), (9), (10)이 사용된다. 이때 식 (10)은 두 종류의 수소에 각각 적용되므로 모두 6개의 식이 되어 원하는 변수들을 모두 구할 수 있다. 그러나 평형 계산에 반복적으로 계산되는 물성들이 상관관계에 의해 온도에 비선형적으로 연결되어 있으므로 반복 계산 방법에 의하여 계산이 수행된다.
본 연구에서는 초기 조건에서 계의 총 부피, 몰수 및 총 내부에너지를 결정한 후 평형 온도를 가정한 후 반복 계산을 통해 수렴시키는 알고리즘을 개발하여 적용하였다. 계산 속도를 높이기 위하여 몰수에 대해 유사한 형식을 보이는 경계 조건들인 식 (2), (7), (8)을 행렬 형식으로 전개하였다.
식 (9)의 우변을 K로 정의한다면 다음과 같이 몰수에 대한 변수의 수를 축소시킬 수 있다.
| (15) |
식 (15)를 이용하여 몰수에 대한 일차 연립방정식들인 식 (2), (7), (8)을 다음과 같이 간략하게 행렬 형식으로 구성할 수 있다.
| (16) |
평형에서의 압력은 위 식으로부터 몰수들이 얻어지면 몰수로부터 계산되는 액상 조성을 이용하여 각 성분에 대한 식 (10)의 합으로 결정된다.
| (17) |
이렇게 계산된 압력은 전압(total pressure)이기 때문에 기-액 평형 관계를 포함하고 있지 않다. 따라서분압(partial pressure)에 대한 관계식인 식 (10)에서 계산된 압력과 비교하여 오차가 수렴할 때까지 온도를 변화시키며 반복 계산을 수행하였다.
모델에 적용된 계산 알고리즘은 순서도 형식으로 Fig. 8에 표현되었다.
3.3 평형에 의한 온도 및 압력 변화 평가
Table 5의 초기 조건으로부터 평형에 도달하였을 때 온도 변화는 Fig. 9에 도시되었다. 초기에 액상 o-H2의 양이 많은 조건(높은 초기 액상 부피비 및 낮은 액상 p-H2 조성)에서는 o-H2의 p-H2로의 전환에 의하여 온도 상승이 높은 경향을 보이고 있다.
액상에서 p-H2의 조성이 95%인 경우에는 고려하고 있는 초기 액상 부피비의 전 영역에서 최종 온도가 임계 온도보다 낮은 것으로 나타났다. 그러나 이외의 조건에서는 초기 액상 부피비가 증가함에 따라 액상에 존재하는 o-H2의 p-H2로의 전환 과정에서 발생하는 열량에 의해 높은 초기 액상 부피비에서는 임계 한계 이상인 영역으로 기-액 상평형을 형성하지 못하였다. 특히 초기 액상에서 p-H2 조성이 25%일 때에는 초기 온도 22 K, 초기 액상 부피비가 0.1인 경우를 제외하면 모든 조건에서 초임계가 되어 단일상으로 존재할 것으로 예상되었다.
고립계에서 온도가 상승하면 고정된 계의 경계면에 의하여 팽창할 수 없기 때문에 압력이 급격히 상승하게 된다. 수소 이성질체 사이의 전환 반응에 의하여 액화 수소 저장 탱크의 압력 변화는 Fig. 10과 같이 추산되었다.
압력 상승은 발열 반응에 의한 온도 상승과 밀접한 관계가 있으므로 Fig. 10의 거동은 Fig. 9와 유사하게 높은 초기 액상 부피비와 낮은 액상 p-H2 조성에서 크게 상승하는 것으로 나타났다.
세 온도 조건(22, 26, 30 K)에서 초기 압력은 각각 1.634, 4.036, 8.229 bar로 모델에서는 임계 온도 근처까지 계산을 수행하였으나 실제 상용 수소 저장 탱크는 22 K의 포화 온도 영역(Fig. 9[a], Fig. 10[a])에서 사용될 것으로 예상된다.
상용 액체 수소 저장 탱크는 안전성을 위하여 과도한 압력 상승 시 압력을 분출하는 안전밸브를 장착하고 있다. Fig. 10(a)에서 보인 것과 같이 액상에서 p-H2 조성이 95% 수준인 상태에서는 탱크 내 수소의 저장량에 무관하게 평형에 도달하여도 압력 상승은 크지 않은 것으로 판단된다. 그러나 수소 액화 공정에서 촉매의 성능 저하 등으로 인하여 o-H2의 조성이 높아지면 적은 양의 액화 수소 충전으로도 안전밸브의 작동 압력에 도달할 가능성이 높아지며 저장되는 액체의 양을 증가시키기 어려워진다.
본 연구에서는 o-H2의 p-H2로의 전환 속도는 고려하지 않았으며 평형 상태를 기준으로 판단하고 있기 때문에 압력 상승 속도에 대해서는 검토하지 않고 있다. 그러나 평형 상태는 압력의 최대 한계를 추산할 수 있는 방법이기 때문에 안전성 측면에서 반드시 고려되어야 할 기준이다.
3.4 액체 부피 변화 평가
수소의 전환 과정에서 증기가 발생하고 이에 따라 액체의 부피는 변화하게 된다. 액체의 부피는 단순히 감소하지는 않으며 이는 정적 공정(isochoric process)의 특성으로 설명된다.
Table 6은 초기 액상 p-H2의 조성이 95%인 경우에 대해 본 연구에서 고려된 전 영역의 초기 부피 비율과 온도에 따라 최종 평형 상태 액체의 비율을 계산하여 나타낸 결과이다. 초기 충전되는 액체의 비율이 10%, 20%, 30%에서는 모든 온도 조건에서의 최종 평형 상태에서 액체의 부피는 감소하여 o-H2의 p-H2로의 전환 과정에서 발생하는 열량과 이 열량으로 인한 기화 과정을 설명하고 있다. 그러나 초기 액상의 비율이 50-90%일 때에는 초기보다 최종 평형 상태 액상의 비율이 증가하는 것으로 추산되었다. 이 조건들에서도 발열에 의하여 기화가 발생하지만 정적 공정의 특성으로 인하여 제한된 공간에 기상으로 존재하기보다 밀도가 높은 액상으로 존재할 수밖에 없기 때문에 액상의 비율이 증가하게 된다. 보다 쉽게 두 단계로 설명하면 기화에 의하여 액상이 감소하고 기상이 증가하지만 부피가 고정되어 있기 때문에 기상 증가로 압력이 증가하고 이에 따라 다시 액화되는 과정으로 이해할 수 있다.
초기 액상 비율이 40%인 경우에는 초기 온도에 따라 최종 액상 비율이 증가할 수도 있고 감소할 수도 있는 것으로 추산되어 초기 액상 비율 40%는 본 연구에서 액체 부피 변화 경향의 경계에 있는 것으로 판단된다.
4. 결 론
e-H2는 온도에 따라 변화하는 o-H2와 p-H2 사이의 평형 조성으로 존재하게 된다. 본 연구에서는 액체 수소의 저장 안전성을 분석하기 위하여 비평형 상태로 액화된 수소가 평형 포화 상태로 존재하는 기체 수소가 있는 탱크에 저장될 때 o-H2의 p-H2로의 평형 전환에 의하여 변화하는 저장 특성을 분석하였다.
기-액 상평형과 두 수소 사이의 화학 평형에 기초하여 개발된 열역학적 모델에 의해 분석한 결과 액화 공정에서 촉매를 사용하지 않거나 급속한 액화 공정으로 n-H2 조성으로 수소를 액화시켰을 경우에는 저장 탱크 내에서 쉽게 임계 조건을 넘어서는 것으로 나타났다.
초기 액상의 p-H2 조성이 높아지면 최종 평형 상태에서 안정적인 기-액 상평형을 형성하는 조건이 확대되는 것으로 파악되었다. 초임계 상태에서는 저장 탱크에 연결되어 있는 펌프 작동에 문제를 야기할 수 있기 때문에 저장 탱크에 액체 수소를 저장할 경우에는 액화 공정에서 p-H2의 조성을 최대한 높일 필요가 있다.
실제 상업적으로 이용되고 있는 액화 수소 저장 탱크 온도 조건 근처인 22 K에서 계산 결과를 보면 일반적으로 고려되고 있는 저장 탱크의 압력 한계(to 6 bar)에 의해 초기 액상의 p-H2 조성은 75% 이상이 되어야 할 것으로 보인다. 그러나 저장 기간 동안 외부로부터 침입할 열을 생각해 보면 이보다 높은 p-H2 조성이 요구될 것으로 판단된다.
액체 수소 저장 탱크의 저장 안전성을 위해서는 저장 탱크의 압력 상승은 억제되어야 한다. 저장 탱크에 부착된 안전밸브가 정상적으로 작동한다면 수소의 배출에 의하여 압력이 조절되므로 수소의 손실을 피할 수 없게 된다. 따라서 액체 수소 저장 탱크의 압력 상승 요인은 다각적으로 분석될 필요가 있으며 본 연구에서는 비평형 액체 수소의 평형 상태로의 전이 과정에서 발생하는 압력 및 온도 변화를 정량적으로 제시하였다.
본 연구에서는 열역학 모델에 기초하여 개발된 모델을 사용하여 전환 속도를 고려한 압력 상승 속도에 대한 분석은 포함되지 않았다. 그러나 열역학적 평형이 공정의 한계를 결정하기 때문에 단열 성능 해석과 함께 본 연구 결과인 최종 평형 상태에 대한 분석이 수소 액화 공정과 액체 수소 저장 공정을 연계하여 이용될 수 있을 것으로 기대된다.
Acknowledgments
본 연구는 산업통상자원부(MOTIE)와 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 연구 과제이다(No. RS-2022-KP002758).
References
-
M. M. H. Bhuiyan and Z. Siddique, “Hydrogen as an alternative fuel: a comprehensive review of challenges and opportunities in production, storage, and transportation”, International Journal of Hydrogen Energy, Vol. 102, 2025, pp. 1026-1044.
[https://doi.org/10.1016/j.ijhydene.2025.01.033]

-
M. SaberiKamarposhti, H. Kamyab, S. Krishnan, M. Yusuf, S. Rezania, S. Chelliapan, and M. Khorami, “A comprehensive review of AI-enhanced smart grid integration for hydrogen energy: advances, challenges, and future prospects”, International Journal of Hydrogen Energy, Vol. 67, 2024, pp. 1009-1025.
[https://doi.org/10.1016/j.ijhydene.2024.01.129]

-
F. Qureshi, M. Yusuf, M. A. Khan, H. Ibrahim, B. C. Ekeoma, H. Kamyab, M. M. Rahman, A. K. Nadda, and S. Chelliapan, “A state-of-the-art review on the latest trends in hydrogen production, storage, and transportation techniques”, Fuel, Vol. 340, 2023, pp. 127574.
[https://doi.org/10.1016/j.fuel.2023.127574]

-
A. Chaube, A. Chapman, Y. Shigetomi, K. Huff, and J. Stubbins, “The role of hydrogen in achieving long term Japanese energy system goals”, Energies, Vol. 13, No. 17, 2020, pp. 4539.
[https://doi.org/10.3390/en13174539]

-
T. T. Le, P. Sharma, B. J. Bora, V. D. Tran, T. H. Truong, H. C. Le, and P. Q. P. Nguyen, “Fueling the future: a comprehensive review of hydrogen energy systems and their challenges”, International Journal of Hydrogen Energy, Vol. 54, 2024, pp. 791-816.
[https://doi.org/10.1016/j.ijhydene.2023.08.044]

-
G. Glenk and S. Reichelstein, “Economics of converting renewable power to hydrogen”, Nature Energy, Vol. 4, 2019, pp. 216-222.
[https://doi.org/10.1038/s41560-019-0326-1]

-
M. R. Usman, “Hydrogen storage methods: review and current status”, Renewable and Sustainable Energy Reviews, Vol. 167, 2022, pp. 112743.
[https://doi.org/10.1016/j.rser.2022.112743]

-
S. Bosu and N. Rajamohan, “Recent advancements in hydrogen storage - comparative review on methods, operating conditions and challenges”, International Journal of Hydrogen Energy, Vol. 52, Pt. C, 2024, pp. 352-370.
[https://doi.org/10.1016/j.ijhydene.2023.01.344]

-
L. Mulky, S. Srivastava, T. Lakshmi, E. R. Sandadi, S. Gour, N. A. Thomas, S. S. Priya, and K. Sudhakar, “An overview of hydrogen storage technologies - key challenges and opportunities”, Materials Chemistry and Physics, Vol. 325, 2024, pp. 129710.
[https://doi.org/10.1016/j.matchemphys.2024.129710]

-
C. Tarhan and M. A. Çil, “A study on hydrogen, the clean energy of the future: hydrogen storage methods”, Journal of Energy Storage, Vol. 40, 2021, pp. 102676.
[https://doi.org/10.1016/j.est.2021.102676]

-
L. Yin, H. Yang, and Y. Ju, “Review on the key technologies and future development of insulation structure for liquid hydrogen storage tanks”, International Journal of Hydrogen Energy, Vol. 57, 2024, pp. 1302-1315.
[https://doi.org/10.1016/j.ijhydene.2024.01.093]

-
J. W. Leachman, R. T. Jacobsen, S. G. Penoncello, and E. W. Lemmon, “Fundamental equations of state for parahydrogen, normal hydrogen, and orthohydrogen”, Journal of Physical and Chemical Reference Data, Vol. 38, No. 3, 2009, pp. 721-748.
[https://doi.org/10.1063/1.3160306]

-
P. Xu, J. Wen, K. Li, S. Wang, and Y. Li, “Review of the continuous catalytic ortho-para hydrogen conversion technology for hydrogen liquefaction”, International Journal of Hydrogen Energy, Vol. 62, 2024, pp. 473-487.
[https://doi.org/10.1016/j.ijhydene.2024.03.085]

-
S. Wijnans, R. Zietara, E. Pearson, M. Boele, and M. A. Reynolds, “Ortho- to para-hydrogen conversion kinetics: new experimental data and an industrial perspective”, Industrial & Engineering Chemistry Research, Vol. 63, No. 46, 2024, pp. 20065-20078.
[https://doi.org/10.1021/acs.iecr.4c02059]

-
S. Sohn and S. H. Yoon, “A study on the catalytic ortho-para hydrogen conversion in the cryogenic heat exchanger filled with catalysts for hydrogen liquefaction”, Journal of Hydrogen and New Energy, Vol. 32, No. 3, 2021, pp. 180-188.
[https://doi.org/10.7316/KHNES.2021.32.3.180]

-
R. W. Harkness and W. E. Deming, “The equilibrium of para and ortho hydrogen”, Journal of the American Chemical Society, Vol. 54, No. 7, 1932, pp. 2850-2852.
[https://doi.org/10.1021/ja01346a503]

-
A. Van Itterbeek, O. Verbeke, F. Theewes, K. Staes, and J. De Boelpaep, “The difference in vapour pressure between normal and equilibrium hydrogen. Vapour pressure of normal hydrogen between 20°K and 32°K”, Physica, Vol. 30, No. 6, 1964, pp. 1238-1244.
[https://doi.org/10.1016/0031-8914(64)90114-4]

-
P. C. Souers, C. K. Briggs, J. W. Pyper, and R. T. Taugawa, “Hydrogen vapor pressures from 4 to 30 K: a review”, U. S. Energy Research & Development Administration, 1977.
[https://doi.org/10.2172/7110677]

-
National Institute of Standards and Technology (NIST), “NIST Chemistry WebBook”, NIST, 2025.
[https://doi.org/10.18434/T4D303]

- J. G. Chung, “Prediction of vapor pressure of parahydrogen from the triple to the critical point”, Journal of the Korean Chemical Society, Vol. 45, No. 4, 2001, pp. 293-297. Retrieved from https://www.dbpia.co.kr/journal/articleDetail?nodeId=NODE11543097, .