Aspen Custom Modeler를 이용한 순산소 PEMFC 재순환 성능 분석
2025 The Korean Hydrogen and New Energy Society. All rights reserved.
Abstract
Hydrogen-oxygen fuel cell has less inertia forces of reactant gases to remove condensed product water by electrochemical reaction that results in electrode flooding. It is resolved by purging with dead-end operation or higher stoichiometric flow rate with recirculation. In this study, the performance of pure oxygen fuel cell system is evaluated with increasing stoichiometric flow rate by recirculation. After the pure oxygen stack and membrane humidifier model is developed by Aspen Customer Model®, the models are implemented as library of Aspen Plus for System Simulation®. Also, four different system layouts are simulated. The results show that a recirculation system without humidifiers is effective in achieving comparable performance, while simplifying system.
Keywords:
Pure oxygen, Proton exchange membrane fuel cell, Flooding, Reciculation system, Stoichiometric ratio키워드:
순산소, 이온 교환막 연료전지, 전극 침수, 재순환 시스템, 화학량론비1. 서 론
세계 각국은 지구 온난화의 주요 원인인 온실가스 배출을 줄이기 위한 정책들을 시행 중이며 규제의 강도는 점점 강화되고 있다. 특히 Jang 등1)은 수송 부문의 수소 에너지로의 전환은 탄소중립 기여도가 매우 높다고 하였는데 수소 전동화는 양이온 교환막 연료전지(proton exchange membrane fuel cell, PEMFC)를 적용하며 낮은 작동 온도, 출력 변동 대응성, 높은 전력 밀도 등의 장점이 있다. 하지만 물 관리와 열 관리는 기술 난도가 높으며 출력 밀도 또한 추가적 개선이 필요한 것으로 알려져 있다2). 특히 출력 밀도를 높이기 위하여 물 관리에 적용되던 외부 가습기를 제거하는 기술도 개발 중이다3).
가습기 제거 연구는 주로 내부 자가 가습에 집중하였다. Williams 등4)은 내부 가습 시 최적 셀 온도와 셀 온도별 적정 음극 화학량론을 조사하였고 Büchi와 Srinivasan5)은 PEMFC 장시간 가동 시 가습기 유무 비교를 통해 자가 가습용 셀의 작동 온도 범위와 내부 가습의 타당성을 지적하였지만 가습기가 적용된 경우보다 출력이 저하됨을 확인하였다. 더불어 내부 가습의 부족한 가습량을 시스템적으로 보완할 수 있는 방법으로 재순환 시스템을 제시하였다. Konno 등6)은 연료전지 시스템의 수소극 배출 가스를 재순환하여 수분을 얻는 방식을 연구하였다. 또한 공기극 재순환 연구도 진행되었는데 Rodosik 등7)은 다양한 부하와 화학양론을 비롯한 많은 조건에서 조사를 수행하였고 최적 재순환 비율을 제시하였다. 이 외에도 Chen 등8)은 공기가 산화제인 경우 질소의 교차 및 축적으로 인해 스택의 성능이 저하됨을 지적하였다.
한편 산화제로 순산소(pure oxygen)를 사용하는 PEMFC는 주로 우주용 동력원이나 수중 이동체를 위하여 개발되고 있다. 순산소 PEMFC는 질소에 의한 성능 영향도 없고 반응성이 좋다는 장점이 있다. 수중 이동체용 순산소 PEMFC는 연료 이용률을 높이기 위한 밀폐 모드(dead end mode)와 수분량 조절을 위한 퍼징 전략에 대한 연구들이 진행 중이다. 특히 Fan 등9)은 수소/산소의 무가습 재순환과 밀폐 모드를 이용하여 수분 관리 및 연료 이용률을 매우 높이는 연구를 진행하였다. 순산소 PEMFC 연구들은 밀폐 시스템 특성상 퍼징 전략 연구가 활발히 진행되고 있으나 재순환율에 따른 영향에 대한 연구는 미흡하다. 또한 순산소 이용 시 낮은 산소 양론비에서 수분 배출 구동력이 부족하여10) 전극 침수가 일어날 수 있어 수분 관리가 매우 중요하지만 아직 관련 연구도 미흡하다.
따라서 본 연구에서는 H2-O2 기반의 PEMFC의 전기 화학 반응에 의한 성능을 모사하고 생성수 발생량을 예측할 수 있는 모델을 개발하고자 한다. 또한 공기 스택의 경우 산소 1몰이 요구될 때 통상 4.76몰의 공기가 필요하다는 점을 고려하여 순산소 스택의 양론비와 수분량에 따른 내부 수분 특성과 성능 변화를 분석하고자 한다. 여기에 수소극과 산소극의 재순환 시에는 양단의 양론비가 증가하기 때문에 양론비 공급 및 가습 성능 영향을 예측하고자 재순환 시스템을 구성하였고 외부 막 가습기가 있는 구성과 없는 구성을 비교하였다. 최종적으로 스택의 입구 조건에 따른 성능과 액체 발생량을 예측하고자 하며 재순환 시스템 적용 시 적절한 운전 조건 및 시스템 구성을 정적 모델을 통해 알아보고자 한다.
2. 모델 개발
본 연구는 화학 공정 모사 프로그램인 Aspen Plus® (AspenTech, Bedford, MA, USA)를 이용하여 해석을 진행하였으며 Aspen Plus®에는 수소 연료전지와 외부 막 가습기 라이브러리가 존재하지 않기 때문에 Aspen Custom Modeler® (AspenTech)를 이용하여 모델링하였다.
2.1 H2-O2 스택 모델
PEMFC는 내부에 다수의 채널을 통해 반응물이 소모되는 동시에 수분이 발생하며 이 중 일부는 전해질막을 통해 반대 측 전극으로 이동하게 된다. 수분을 포함한 가스 종의 농도는 채널을 통과하며 변화한다. 하지만 산소 스택의 경우 산소극 운동량이 낮아서 응축된 수분을 외기로 배출하기 위한 충분한 관성을 확보할 수 없는 것으로 알려져 있다. 이에 따라 전극 침수 발생 빈도가 높고 전극 침수에 의한 성능 저하가 큰 것으로 알려져 있다. 본 연구에서는 채널 길이 방향 차분화를 통해 액체 발생량을 확인하고자 하였다. 유동은 채널 방향과 전해막 방향을 고려하여 2차원 모델로 개발하였다. 모델에 적용한 가정은 다음과 같다.
첫째, 가스는 정상 상태 이상기체를 가정한다. 둘째, 스택은 외부와 단열되어 있다. 셋째, 스택 내부에서 압력 손실은 무시한다. 넷째, 유량, 온도, 압력을 통해 액체 발생량만을 계산하며 액체 발생에 의한 영향은 무시한다. 다섯째, 반응물은 모든 채널에 고르게 분배되며 수소극/산소극 유동은 평행류이다.
수소극 채널, 산소극 채널, 냉각수 채널 내 유동은 차분식을 적용하였다. 수소 반응량은 전류 밀도를 이용하여 계산할 수 있다11).
| (1) |
식 (1)의 아래첨자 i는 노드 번호이며 반응 면적을 노드 개수로 나누어 수소 반응량을 계산한다. 채널을 흐르는 유체의 종 보존 방정식은 다음과 같이 결정된다12).
| (2) |
| (3) |
| (4) |
H2, O2는 각각 수소극, 산소극에만 흐르고 Ṅdrag와 Ndiff는 전해질막을 통한 물의 이동을 표현하며 채널의 수분 흐름을 위와 같이 나타낼 수 있다. 이때 수소극에서 산소극으로 이동하는 방향을 양의 방향이라고 가정하고 Ndrag는 H+ 이온이 막을 투과할 때 전기 삼투 현상에 의하여 이동하는 수분량을 나타낸다11).
| (5) |
Ṅdiff는 두 전극 간의 수분 농도 차이에 의한 역확산량을 나타낸다. 역확산에 의한 수분 이동은 전해질막의 물성치와 역확산계수 및 전극 간 수분 함량 차를 이용하여 표현할 수 있으며11) 역확산계수는 셀 온도와 전해질막 수분 함량을 통해 구할 수 있다13). 이때 수분 함량 λ는 수분 활성도로 계산할 수 있으며 14 이상에서 과포화 상태이기에 액상이 발생할 수 있고 80℃에서 16.8까지 도달할 수 있다11).
| (6) |
셀 전압은 이론 전압으로부터 손실을 빼서 결정하였다. 전압 손실은 활성화 손실, 저항 손실, 농도 손실을 고려하여 결정하였다.
| (7) |
이론 전압은 Nernst 전압으로 셀 온도와 반응물 분압으로 계산된다14). 활성화 손실은 반응속도에 의하여 발생하며 산소극의 영향이 매우 크다고 알려져 있기에2) 산소극 측만 고려하였고 헨리의 법칙에 의하여 계산된 cO2ref와 유효 확산계수(DO2eff) 및 교환 전류 밀도 항(Ai0)의 식으로 계산하였다15).
| (8) |
저항 손실은 이온 전도도와 전해질막 두께를 이용하여 계산하였다. 이온 전도도는 전해질막의 수분함량과 셀 온도로 계산할 수 있다16).
| (9) |
농도 손실은 전류 밀도와 산소 분압, 셀 온도 및 최대 전류 밀도로 표현된 모델을 적용하였으며 c2는 상수이다14).
| (10) |
열전달 모델은 채널 내 가스, 냉각수 및 반응에 의한 발생열만을 고려하고 연료전지 온도는 모든 노드에서 동일하며 핀에 의하여 확장된 표면의 열전달로 가정하여 계산하였다17). 지배방정식은 에너지 보존 법칙으로부터 식 (11)과 같이 나타낼 수 있다. 또한 셀 온도와 국부 유체 온도, 열저항에 대한 식으로 나타낼 수 있으며 핀과 내부 강제 대류 모델이 복합된 식으로 계산된다18).
| (11) |
| (12) |
| (13) |
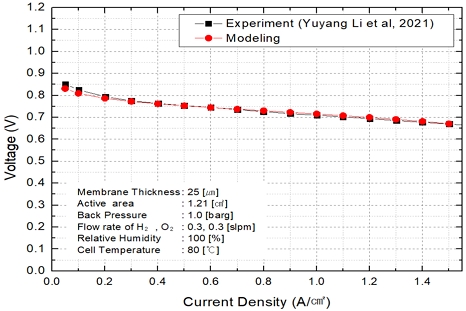
순산소 연료전지 모델은 성능 실험과 비교하여 신뢰성을 검증하였으며 결과는 Fig. 1과 같이 나타났다19). 해석 조건은 실험 조건과 동일하게 적용하였고 해당 전류 밀도 구간에서 root mean squared error (RMSE) 기준 0.00759, mean absolute percentage error (MAPE) 기준 0.728%의 오차를 보였다. 순산소를 이용하는 경우 질소가 존재하지 않아 적은 수분 공급만으로 높은 수분 함량을 보이는 특징을 갖기에 해석 조건의 상대 습도 조건으로도 대표성을 가질 수 있다.
2.2 막 가습기 모델
본 연구에서는 막 가습기 유무에 의한 영향을 분석하기 위하여 액체/증기(liquid to gas) 다중 노드 막 가습기를 모델링하였다20). 원통 다관형 막 가습기의 열전달량은 effectiveness number of transfer unit (ε-NTU) 방법으로 구하였으며 가스가 흐르는 방향을 따라 유한차분법을 적용하였다. 종 보존 방정식은 수분함량 및 몰 유량을 이용하여 적용하였다. 또한 Nafion®막을 채용한 막 가습기를 적용하고 수분 이동 모델은 다음과 같이 구하였다.
| (14) |
| (15) |
| (16) |
수분 투과막의 온도는 열용량이 큰 액체 흐름의 온도로 가정하였으며 λliq는 실험을 통해 상수 15.6으로 나타난다20). 에너지 보존 및 열전달 모델은 원통 다관형 열교환기를 적용하였고 ε-NTU 방법을 통해 온도를 계산하였다18). 또한 ε은 질량 유량에 의하여 많은 영향을 받으며 본 연구에서는 0.95로 고정하였다21).
| (17) |
2.3 시스템 구성
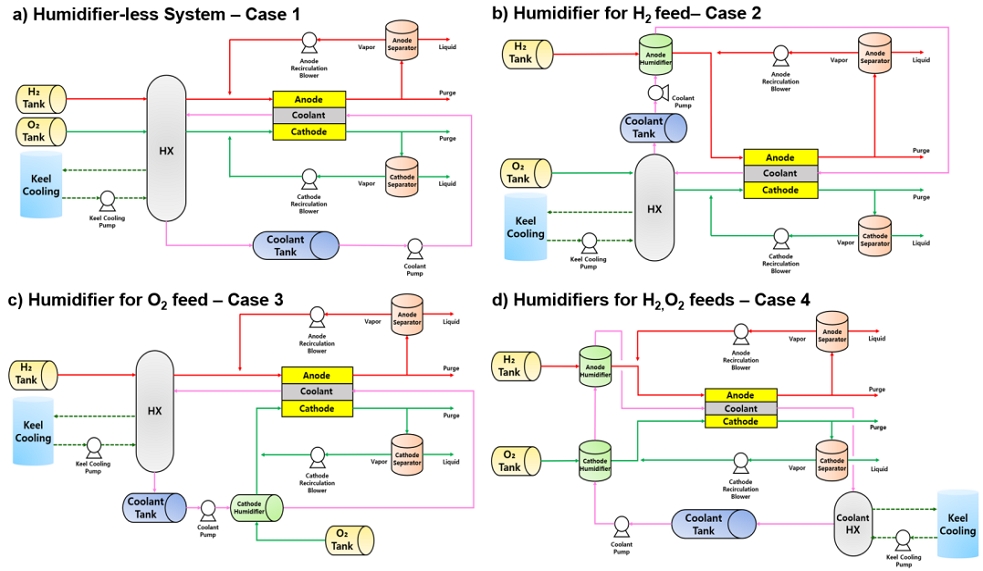
시스템 해석을 위해서는 순산소 PEMFC 스택뿐 아니라 산소 공급계, 수소 공급계, 열관리계 등 구성 요소들이 필요하다. 본 연구에서는 효율적인 해석을 위해서 막 가습기와 산소 스택 모델을 제외한 시스템 구성품은 Aspen Plus®의 라이브러리를 통해 결정하였다. 산소 스택과 가습기의 형상 조건은 Table 1, 시스템 운전 조건은 Table 2, 구성품 운전 조건은 Table 3에 표시하였다. 또한 일반적으로 PEMFC 시스템의 냉각수 온도는 라디에이터를 통해 조절되지만 본 연구에서는 선박이나 잠수정 등에 적용되는 선체 외부 냉각 시스템으로 구성하였다22). 통상 재순환 블로워의 압력 상승은 상대적으로 크지 않아 재순환 유체 출구의 온도가 높지 않다. 이 경우 순산소 공급 시스템으로부터 유입되는 가스와 혼합으로 스택 입구에서 응축수가 발생할 수 있다. 본 연구에서는 크게 4가지 레이아웃을 분석하고자 하였고 산소극과 수소극 양단에 재순환 시스템을 효과적으로 활용하면서 스택 입구에서의 응축 억제를 고려하였다. Fig. 2(a)의 case 1은 재순환 후 양단 가열하는 레이아웃이고 Fig. 2(b)는 case 2 레이아웃으로 수소극 재순환 및 수소 가습을 통한 승온과 산소극의 별도 가열이며 Fig. 2(c)의 case 3은 산소극 재순환 및 산소 가습을 통해 승온하고 수소는 별도 가열한다. Fig. 2(d)는 case 4로 양단 재순환하는 동시에 별도 가습하는 경우를 도시하였다.
3. 결과 및 고찰
3.1 공기 독립형 산소 스택 특성 분석
공기 PEMFC 스택의 경우 수소 2몰 반응 시 요구되는 산소량은 1몰이지만 공기 기준 4.76 몰이 필요하다. 하지만 산소 스택에서는 수소 2몰 기준 1몰의 산소만이 요구되므로 유체의 관성력 차에 따른 수분 제거 능력이 부족하다. 이러한 산소 스택의 가스 재순환은 수분 제거를 위한 관성력 확보 차원에서 유리할 것으로 보인다. 더불어 산소 재순환을 통해 산소 농도를 높일 수 있기 때문에 성능 향상도 기대할 수 있다. 본 연구에서는 스택의 양론비 증가에 따른 스택 내부 변화를 확인하기 위하여 수소극/산소극 양론비가 각각 2.0/2.0, 2.0/9.5, 9.5/2.0, 9.5/9.5일 때 스택 성능과 액적 생성 특성을 확인하였다.
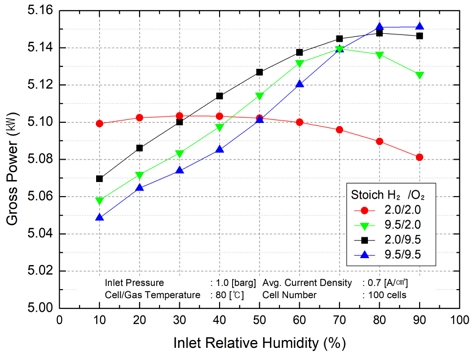
Fig. 3과 Fig. 4는 순산소 스택의 수소극과 산소극 양단의 입구 가스 온도가 80℃로 유지되고 상대 습도를 양쪽 모두 동일하게 높인 경우에 스택의 성능과 채널 내 증기 응축 특성을 보여주고 있다. 먼저 Fig. 3에는 입구 상대 습도 변화에 따른 스택 성능 변화를 도시하였다. 스택 성능은 양단의 양론비를 2.0으로 유지하는 경우를 제외하고는 입구 상대 습도에 따라 성능이 증가하는 경향을 보여주고 있다. 스택으로 유입되는 수소와 산소의 양론비를 2.0으로 유지한 경우는 입구 상대 습도가 30% 이하에서는 4개의 양론비 조건 중 가장 높은 출력을 보이고 있으나 상대 습도를 40% 이상으로 상승시킨 경우 다른 양론비 조합과 다르게 출력이 감소하는 것을 볼 수 있다. 양론비 2.0 조건에서는 입구 상대 습도 30%에서 수분 공급을 통한 전해막 저항 손실 감소 효과가 크지만 그 이상으로 상대 습도를 증가시키는 경우 반응물 농도 감소로 인해 성능이 서서히 감소하는 것을 알 수 있다.
산소극의 양론비를 9.5로 상향시킨 경우 반응 활성이 개선되어 이론 전압이 개선된다. 따라서 반응 손실은 최소화되는 경향을 보이므로 입구 상대 습도 증가에 따른 전해막 이온 저항이 감소하고 출력 특성이 선형적으로 상승하는 것을 볼 수 있으며 액적 생성의 영향으로 높은 상대 습도에서는 출력이 일정하게 유지되고 있다. 이에 비해 수소극 양론비만 9.5로 상향시킨 경우 산소극의 활성도가 제한적으로 증가하는 상황에서 입구 상대 습도 증가로 인하여 수분 농도가 지속적으로 상승하면서 고습 조건에서 산소의 상대 농도가 감소하게 되고 출력이 다시 감소하는 것을 볼 수 있다.
마지막으로 양론비 9.5/9.5는 높은 양론비로 인하여 양단의 가습 효과가 상대적으로 줄어들게 되고 수분 함량이 비교적 낮아지기에 대부분의 구간에서 출력이 가장 낮았지만 입구 상대 습도 80% 이상에서는 가장 높은 출력을 보였다.
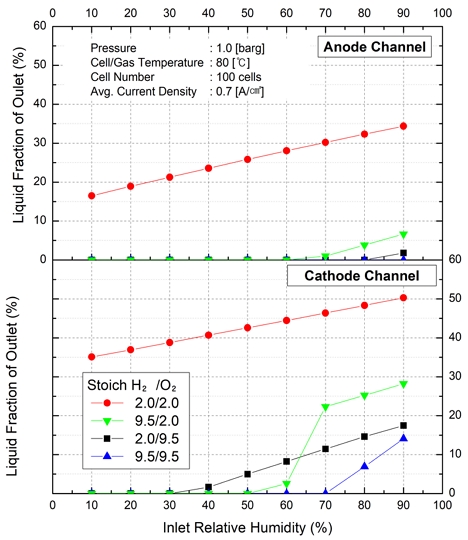
수소극과 산소극의 양론비를 증가시킬 때 양단 응축수의 액체 분율을 Fig. 4에 도시하였다. 본 연구에서는 수증기의 증기압이 포화 수증기압 이상으로 높아지면 상평형에 의하여 액상이 형성되는 것으로 가정하였다. 따라서 액체 분율은 해당 질량 유량만큼 수증기가 응축되는 것을 의미하며 출구에서 액체 분율이 높아질수록 스택 내부에 플러딩이 발생할 확률이 커진다고 볼 수 있다23). 양단의 양론비를 2.0으로 유지한 경우 입구의 상대 습도가 매우 낮은 수준에서도 스택 출구의 액체 분율이 높아지는 것을 볼 수 있다. 양론비가 낮은 경우 스택 내부에서 전기 화학반응에 의해 소모되는 가스만큼 수증기가 발생하게 됨과 동시에 가스의 몰 농도가 낮아지게 된다. 이때 과다하게 발생한 수증기로 인하여 수소극과 산소극의 증기압이 포화 수증기압 이상으로 증가하게 되면서 응축이 진행되는 것으로 볼 수 있다. 하지만 상대적으로 높은 양론비에서는 전기 화학 반응을 통해 일정량의 가스가 사용되더라도 가스의 몰 농도가 일정 수준 이상으로 유지되기 때문에 출구에서의 액체 분율이 매우 낮은 것을 알 수 있다. 특히 수소극의 경우 전기 화학 반응이 발생하지 않기에 수증기 농도는 입구 유입 수증기와 산소극으로부터 이송된 수증기량에 의존하며 양론비가 높은 경우 대부분의 입구 상대 습도에서도 전극 침수가 발생하기 어려운 수준의 액체 분율이 관찰된다.
수소극의 양론비만 9.5로 높인 경우 산소극에서 상대적으로 높은 액체 분율이 관찰되는 것을 볼 수 있다. 이는 산소극 양론비가 2.0으로 매우 낮은 상태에서 산소 소모량에 해당하는 만큼 수증기 분율이 증가하면서 발생한 현상으로 볼 수 있다. 즉 산소극 입구 상대 습도가 낮은 상태에서도 전기 화학 반응에 의하여 수증기 분압은 증가하지만 입구 상대 습도 70% 이상의 조건이 되면 포화 수증기압 이상의 증기 발생량이 급격히 증가하면서 액체 분율이 증가하는 것으로 볼 수 있다. 이러한 액체 분율의 증가는 상대 습도 60% 조건에서도 일부 관찰되지만 70% 조건부터는 과포화 상태가 뚜렷해지는 것으로 판단된다. 양단의 양론비를 9.5로 유지한 경우에는 입구 상대 습도 70% 이상의 조건에서부터 포화 증기압 이상의 증기압 증가가 나타나고 이에 따라 액체 분율이 증가하는 것도 볼 수 있다. 또한 수소극과 산소극의 출구 액체 분율의 크기가 다른 것도 확인할 수 있는데 이는 전기 화학 반응에 의한 생성 수가 산소극 쪽에서 발생하기 때문에 액체 분율도 수소극보다 산소극에서 더 높은 것을 보여준다.
3.2 재순환 시스템 분석
순환을 포함하는 산소 스택 시스템은 수소극과 산소극 출구에서 배출되는 가스 혼합물 중 응축수는 기수 분리기를 거쳐 일정 부분 제거하고 재순환 블로워를 통해 산소극/수소극 공급 가스와 혼합되게 된다. 기수 분리기를 거치면서 일정 부분 온도(해석 온도 75℃) 강하가 발생하게 되며 재순환 블로워의 압력 상승분이 크지 않기 때문에 재순환 블로워를 통과한 가스 혼합물의 온도는 스택 출구단 대비 낮아질 것으로 보인다. 여기에 산소극과 수소극 반응 가스가 저온으로 혼합되기 때문에 산소극과 수소극 유입 전 재순환 가스와 혼합 시 추가적인 온도 강하가 발생하고 이에 따라 응축수 발생 가능성이 높아지게 된다.
따라서 본 연구에서는 스택 입구단 유입 시 응축이 발생하지 않도록 4가지 각기 다른 레이아웃을 선정하고 해석을 진행하였다. Case 1의 경우를 기준 레이아웃으로 볼 수 있으며 case 4에는 외부 가습기를 설치하고 재순환 블로워도 포함시켜 가습기 유무 차이를 명확하게 비교할 수 있도록 하였다. 또한 재순환 유량에 따른 시스템 성능 변화를 확인하기 위하여 재순환 유량은 스택 입구에서의 양론비를 통해 파악하였으며 두 전극의 양론비는 서로 동일하게 설정하였다. 이때 스택만을 대상으로 한 해석과 다르게 양론비가 커진다는 것은 재순환 유량이 많아진다는 것을 의미하며 결과적으로 더 많은 수분과 반응물이 유입된다. 재순환이 없는 경우 양론비는 두 전극 모두 1.1이며 막 가습기는 재순환 유체가 아닌 연료 탱크로부터 나오는 유체만을 가습하도록 레이아웃을 설계하였다.
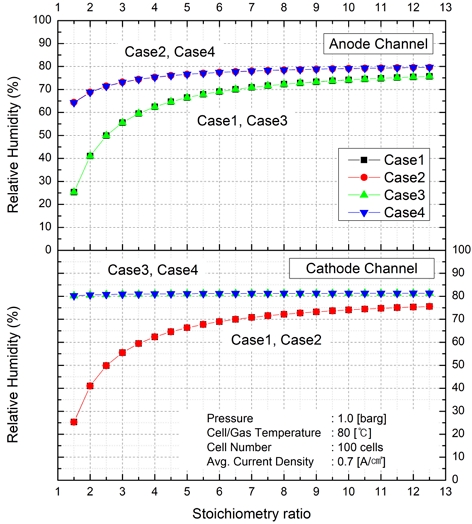
재순환에 따른 연료전지 스택 입구 상대 습도의 변화와 출력 변화는 Figs. 5, 6에 도시하였다.
먼저 Fig. 5에는 수소극 입구와 산소극 입구 상대 습도를 보여준다. 반응 가스를 재순환 가스와 혼합하게 되면 재순환 유량 변화에 따른 온도 및 포화 증기압의 변화로 상대 습도를 통해 수분량을 비교하기 힘들다. 따라서 스택 입구에서의 온도를 스택 작동 온도인 80℃로 가정하여 상대 습도를 비교함으로써 수분 유입량과 재순환 유량의 상관관계를 볼 수 있도록 하였다. 이때 기수 분리기는 작동 온도에서 포화 상태를 유지하기 때문에 재순환 가스는 기수 분리기 작동 온도(75℃)에서 100% 상대 습도로 재순환 된다.
수소극에서 case 1과 3은 재순환을 통해서만 수분을 공급받기 때문에 저양론비와 고양론비에서의 습도 차이가 비교적 크게 나타난다. 이에 비해 case 2와 4의 경우는 외부 가습기에서 수소극 반응 가스를 가습하기 때문에 case 1과 3 대비로 습도가 높지만 재순환 유량에 따른 차이는 비교적 적은 것을 볼 수 있다. 산소극 또한 반응용 산소를 별도로 가습하는 경우(case 3, 4)는 재순환을 통해서만 가습하는 경우(case 1, 2) 대비 상대 습도가 큰 것을 볼 수 있다. 한편 case 3, 4의 산소극 입구 상대 습도는 낮은 양론비 구간에서 case 2, 4의 수소극과 선형의 차이가 나타나는 것을 볼 수 있다. 이는 가습기를 통과하는 feed 가스의 유량이 양론비 기준으로 설정되어 있기에 산소는 수소의 1/2 유량이 흐르지만 가습량은 수분함량 차이로 결정되기 때문에 재순환을 통한 가습을 적게 받는 양론비 구간에서 두 전극의 상대 습도 차이가 발생하는 것을 보여준다. 마찬가지로 재순환 유량이 커질수록 재순환을 통한 가습 효과를 많이 받게 되면서 두 전극의 입구 상대 습도는 기수 분리기 출구의 조건에 점차 수렴하게 된다.
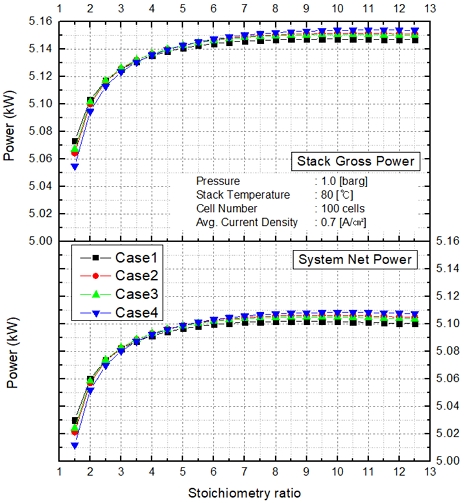
Fig. 6은 재순환 유량 변화에 따른 양론비 변화에 대한 시스템 출력 변화를 보여주고 있다. 양론비 4 이하의 구간에선 무가습 조건인 case 1이 가장 큰 출력을 보이며 두 전극을 모두 가습하는 case 4는 가장 낮은 출력을 보인다. 이는 외부 막 가습기에 의한 수분 공급이 반응물의 농도를 낮추기 때문이다. 또한 모든 case에서 재순환 유량을 올릴수록 출력이 증가하며 양론비가 7보다 커지면 거의 일정하게 유지된다. 시스템 순 출력(system net power)은 운전 장치(balance of plant, BOP) 요구 동력을 고려하여 시스템에서 얻을 수 있는 출력을 보여주고 있는데 스택 생산 전력(gross power) 중 1% 미만의 전력을 사용하기 때문에 스택 생산 전력과 동일한 양상을 보여주고 있다. 하지만 양론비를 9 이상으로 높일 때 재순환 유량 증가에 의한 기생 전력 소모량에 비해 스택 생산 전력 증가량이 줄어들어 순 출력의 감소를 나타낸다.
4. 결 론
본 연구에서는 Aspen Custom Modeler®를 이용하여 차분형 순산소 PEMFC 모델과 막 가습기 모델을 개발하였으며 Aspen Plus®를 통하여 시스템 해석을 진행하였다. 그 결과 다음과 같은 결론을 얻었다.
- 1) 순산소 PEMFC는 양론비가 낮을 때 전기 화학 반응에 의한 생성 수의 응축 가능성이 높아진다. 특히 수소극 대비 산소극에서 액체 분율이 크게 관찰되었으며 수소극보다 산소극의 양론비를 높이는 것이 출력을 높이고 액체 분율을 줄이는 데 더 효과적으로 나타났다.
- 2) 재순환 유량이 커질수록 모든 구성에서 입구 성분은 기수 분리기 출구 조건과 수렴하며 생산 전력과 순 출력이 증가하지만 9 이상의 재순환 양론비에서는 높은 양론비로 인한 스택 내부의 평균 수분 함량의 감소로 출력 감소가 발생한다.
- 3) 시스템 레이아웃별 시스템 순 출력은 재순환 양론비 5 이상일 때 case 1이 가장 낮고 case 4가 가장 높지만 구성 간의 출력 차이는 0.2% 미만으로 매우 작은 수준이다.
Nomenclature
| A : | 면적(cm2). |
| : | 몰 유량(mol/s). |
| I : | 수소 반응량(mol/s). |
| L : | 길이(cm). |
| D : | 확산계수(cm2/s). |
| T : | 온도(K). |
| P : | 압력(bar). |
| J : | 전류 밀도(A/cm2). |
| R : | 열저항(K/W), 기체상수(J/K-mol). |
| V : | 전압(V). |
| t : | 두께(cm). |
| : | 질량 유량(g/s). |
| W : | 출력(W). |
| M : | 단위 몰 당 질량(g/mol). |
| N : | 셀/휜/노드 개수. |
| : | 열 전달률(W). |
| cp : | 비열(J/g-K). |
| C : | 열 용량(W/K). |
| x : | 몰 분율(mol/mol). |
| F : | 패러데이 상수(C/mol). |
| ρ : | 밀도(g/cm3). |
| σ : | 이온 전도도(S/cm). |
| an : | 수소극. |
| cat : | 산소극. |
| cool : | 냉각수 채널. |
| w : | H2O. |
Acknowledgments
본 연구는 2025년 산업통상자원부(MOTIE) 및 산업기술평가관리원(KEIT) 연구비 지원에 의한 연구임(No. 00423040). 본 연구는 산업통상자원부(MOTIE)와 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 연구 과제임(No. 20213030030210).
References
-
S. J. Jang, R. S. Park, Y. H. Choi, and Y. W. Hwang, “An evaluation of net-zero contribution regarding hydrogen energy conversion in urban building and transport sector”, Journal of Hydrogen and New Energy, Vol. 34, No. 2, 2023, pp. 100-112.
[https://doi.org/10.7316/JHNE.2023.34.2.100]

-
R. O'Hayre, S. W. Cha, W. Colella, and F. B. Prinz, “Fuel cell fundamentals”, John Wiley & Sons, USA, 2016.
[https://doi.org/10.1002/9781119191766]

-
H. Park, “Effect of the hydrophilic and hydrophobic characteristics of the gas diffusion medium on polymer electrolyte fuel cell performance under non-humidification condition”, Energy Conversion and Management, Vol. 81, 2014, pp. 220-230.
[https://doi.org/10.1016/j.enconman.2014.02.029]

-
M. V. Williams, H. R. Kunz, and J. M. Fenton, “Operation of Nafion®-based PEM fuel cells with no external humidification: influence of operating conditions and gas diffusion layers”, Journal of Power Sources, Vol. 135, No. 1-2, 2004, pp. 122-134.
[https://doi.org/10.1016/j.jpowsour.2004.04.010]

-
F. N. Büchi and S. Srinivasan, “Operating proton exchange membrane fuel cells without external humidification of the reactant gases: fundamental aspects”, Journal of The Electrochemical Society, Vol. 144, No. 8, 1997, pp. 2767.
[https://doi.org/10.1149/1.1837893]

-
N. Konno, S. Mizuno, H. Nakaji, and Y. Ishikawa, “Development of compact and high-performance fuel cell stack”, SAE International Journal of Alternative Powertrains,Vol. 4, No. 1, 2015, pp. 123-129.
[https://doi.org/10.4271/2015-01-1175]

-
S. Rodosik, J. P. Poirot-Crouvezier, and Y. Bultel, “Impact of humidification by cathode exhaust gases recirculation on a PEMFC system for automotive applications”, International Journal of Hydrogen Energy, Vol. 44, No. 25, 2019, pp. 12802-12817.
[https://doi.org/10.1016/j.ijhydene.2018.11.139]

-
Y. S. Chen, C. W. Yang, and J. Y. Lee, “Implementation and evaluation for anode purging of a fuel cell based on nitrogen concentration”, Applied Energy, Vol. 113, 2014, pp. 1519-1524.
[https://doi.org/10.1016/j.apenergy.2013.09.028]

-
L. Fan, L. Xing, Z. Tu, and S. H. Chan, “A breakthrough hydrogen and oxygen utilization in a H2-O2 PEMFC stack with dead-ended anode and cathode”, Energy Conversion and Management, Vol. 243, 2021, pp. 114404.
[https://doi.org/10.1016/j.enconman.2021.114404]

-
T. V. Reshetenko, G. Bender, K. Bethune, and R. Rocheleau, “Systematic study of back pressure and anode stoichiometry effects on spatial PEMFC performance distribution”, Electrochimica Acta, Vol. 56, No. 24, 2011, pp. 8700-8710.
[https://doi.org/10.1016/j.electacta.2011.07.058]

-
T. E. Springer, T. A. Zawodzinski, and S. Gottesfeld, “Polymer electrolyte fuel cell model”, Journal of The Electrochemical Society, Vol. 138, No. 8, 1991, pp. 2334.
[https://doi.org/10.1149/1.2085971]

-
H. Son, J. Han, and S. Yu, “Development of a multi-physics model of polymer electrolyte membrane fuel cell using Aspen Custom Modeler”, Journal of Hydrogen and New Energy, Vol. 32, No. 6, 2021, pp. 489-496.
[https://doi.org/10.7316/KHNES.2021.32.6.489]

-
A. Kosakian, L. P. Urbina, A. Heaman, and M. Secanell, “Understanding single-phase water-management signatures in fuel-cell impedance spectra: a numerical study”, Electrochimica Acta, Vol. 350, 2020, pp. 136204.
[https://doi.org/10.1016/j.electacta.2020.136204]

- J. T. Pukrushpan, “Modeling and control of fuel cell systems and fuel processors [Doctoral dissertation]”, Ann Arbor (MI): University of Michigan, 2003.
- P. C. Sui, L. D. Chen, J. P. Seaba, and Y. Wariishi, “Modeling and optimization of a PEMFC catalyst layer”, SAE Transactions, Vol. 108, 1999, pp. 729-737. Retrieved from https://www.jstor.org/stable/44743405, .
-
P. Dobson, C. Lei, T. Navessin, and M. Secanell, “Characterization of the PEM fuel cell catalyst layer microstructure by nonlinear least-squares parameter estimation”, Journal of The Electrochemical Society, Vol. 159, No. 5, 2012, pp. B514.
[https://doi.org/10.1149/2.041205jes]

-
S. Yu and D. Jung, “Thermal management strategy for a proton exchange membrane fuel cell system with a large active cell area”, Renewable Energy, Vol. 33, No. 12, 2008, pp. 2540-2548.
[https://doi.org/10.1016/j.renene.2008.02.015]

- Y. A. Çengel and A. J. Ghajar, “Heat and mass transfer: fundamentals and applications”, 6th ed, McGraw-Hill, USA, 2020.
-
Y. Li, P. Zhang, L. Wan, Y. Zheng, X. Qu, H. Zhang, Y. Wang, K. Zaghib, J. Yuan, S. Sun, Y. Wang, Z. Zhou, and S. Sun, “A general carboxylate-assisted approach to boost the ORR performance of ZIF-derived Fe/N/C catalysts for proton exchange membrane fuel cells”, Advanced Functional Materials, Vol. 31, No. 15, 2021, pp. 2009645.
[https://doi.org/10.1002/adfm.202009645]

-
D. Chen, W. Li, and H. Peng, “An experimental study and model validation of a membrane humidifier for PEM fuel cell humidification control”, Journal of Power Sources, Vol. 180, No. 1, 2008, pp. 461-467.
[https://doi.org/10.1016/j.jpowsour.2008.02.055]

-
G. Li, J. Wang, F. Zhang, and J. Liu, “Comprehensive operational parameter analysis of cross-flow hollow fiber membrane humidifier for humidification dehumidification desalination”, Desalination, Vol. 542, 2022, pp. 116066.
[https://doi.org/10.1016/j.desal.2022.116066]

-
J. Han, J. Han, H. Ji, and S. Yu, ““Model-based” design of thermal management system of a fuel cell “air-independent” propulsion system for underwater shipboard”, International Journal of Hydrogen Energy, Vol 45, No. 56, 2020, pp. 32449-32463.
[https://doi.org/10.1016/j.ijhydene.2020.08.233]

-
J. Shen, L. Xu, H. Chang, Z. Tu, and S. H. Chan, “Partial flooding and its effect on the performance of a proton exchange membrane fuel cell”, Energy Conversion and Management, Vol. 207, 2020, pp. 112537.
[https://doi.org/10.1016/j.enconman.2020.112537]