분자 간 상호작용 기반 상변화 모델을 이용한 액체수소 저장용기의 증발가스 발생 평가
2025 The Korean Hydrogen and New Energy Society. All rights reserved.
Abstract
The boiling point of liquid hydrogen is extremely low at 20 K, making it prone to generate boil-off gas (BOG). BOG can lead to a rise in pressure and a potential rupture of liquid hydrogen storage vessels, prompting research on estimating BOG generation using numerical analysis and phase change models. Commonly used models require empirical parameters obtained through trial and error. In this study, a multi-phase fluid flow analysis was conducted on a liquid hydrogen storage vessel to propose a phase change model that does not rely on the empirical parameters. The phase change model based on the intermolecular interactions provided the BOG generation rate of 0.23 kg/day.
Keywords:
Boil-off gas, Intermolecular interaction, Liquid hydrogen, Multi-phase fluid flow analysis, Phase change model, Storage vessel키워드:
증발가스, 분자 간 상호작용, 액체수소, 다상 열유동 해석, 상변화 모델, 저장용기1. 서 론
액체수소는 친환경 연료로 탄소를 배출하지 않고 에너지 밀도가 높다는 장점이 있으나 끓는점이 대기압 상태에서 20 K (-253℃)로 매우 낮아 저장 및 이송 과정 중 열유입에 의해 증발가스(boil-off-gas, BOG)가 발생한다1-3). BOG는 액체수소 저장용기의 압력을 상승시키며 과도한 압력 상승은 저장용기 파열의 원인이 된다4). 저장용기의 파열을 방지하기 위하여 BOG로 인한 압력 상승 그리고 액체수소의 저장 시간 등을 고려한 저장용기 설계가 요구되며 BOG 발생량은 실험 및 열유동 해석을 통해 예측할 수 있다.
Fu 등5)은 직경과 높이가 각각 0.5 및 1 m인 원통형 액체수소 저장용기를 대상으로 Lee 상변화 모델6)을 적용한 다상 열유동 해석을 수행하였다. 해석 조건으로 50, 150 및 250 W/m2의 열유입, 0, 0.0098 및 9.8 m/s2의 중력가속도 그리고 30 %, 50 % 및 80 %의 충진율을 고려하였고 열유입, 중력가속도, 충진율이 클수록 BOG 발생에 의한 저장용기의 압력이 빠르게 상승함을 확인하였다. Wei와 Zhang7)은 지름과 높이가 각각 318 및 508 mm인 원통형 액체수소용 저장용기를 대상으로 슬로싱 거동을 고려한 다상 열유동 해석을 수행하고 실험 결과와 비교하였다. 슬로싱 거동의 진동수는 0.57 Hz였고 BOG 발생량 계산을 위하여 Lee 상변화 모델이 사용되었다. 해석으로 얻어진 시간에 따른 저장용기 내의 압력 변동은 실험 결과 대비 5% 이내의 정확도를 보여주었다. Jeon 등8)은 극저온 연료용 C타입 저장용기를 대상으로 다상 열유동 해석을 수행하고 실험 결과와 비교하였다. 고체-액체 및 액체-기체 계면에 대하여 Lee 상변화 모델을 각각 적용하여 고체-액체 계면에서는 고체 벽면으로부터의 열유입과 경험적 계수를, 액체-기체 계면에서는 잠열과 포화온도를 사용하여 기화율을 각각 계산하였다. 저장용기의 지지대를 통한 열유입은 BOG 발생의 주요 원인이 되었다. 다상 열유동 해석으로 얻어진 BOG 발생률은 4.984%/day로 실험 결과와 0.08% 오차 범위 내에서 일치하였다. Ahammad 등9)은 액체질소 및 LNG의 막비등(film boiling)을 예측하기 위한 모델을 제안하였으며 선행 연구10,11)와 비교하였다. Rayleigh-Taylor 접근법을 적용하여 다상 열유동 해석을 수행하였으며 기포 생성 위치, 크기, 주기 등이 막 두께가 유입되는 열유속에 영향을 미침을 확인하였다. 연구 결과로 얻어진 벽면의 온도에 따른 열유속의 경향은 선행 연구와 유사하였다.
상기 연구 사례는 일반적으로 사용되고 있는 Lee 상변화 모델 및 막비등 모델 기반 다상 열유동 해석의 결과가 실제 실험 결과와 얼마나 유사한지를 보여주고 있다. 그러나 Lee 상변화 모델은 실험을 기반으로 결정되는 경험적 계수를 이용하고 막비등 모델은 기포 크기와 형상에 대한 계수의 조정이 요구되기 때문에 다양한 형상의 저장용기 및 운영 조건에 따라 범용적으로 사용하기에는 어려움이 따른다. 본 연구에서는 액체수소용 저장용기의 BOG 발생량 추정 시 Lee 상변화 모델의 경험적 계수가 필요 없는 새로운 상변화 모델을 제안하였다. 그리고 분자 간 상호작용(intermolecular Interaction)을 고려하여 기화 및 액화의 기준이 되는 에너지와 이의 볼츠만 분포를 이용하여 BOG 발생률과 재액화율(re-liquefaction rate)을 추정하였다.
2. 상변화 모델
2.1 Lee 상변화 모델
수치 해석적 방법으로 액체수소 저장용기의 압력상승률 및 BOG 발생을 추정하기 위해서는 기화(vaporization) 및 액화(liquefaction)와 같은 수소의 상변화 과정에 대한 물리적 모델이 필요하다. 두 상의 경계면에서의 물질 전달식(mass transfer equation)은 통상적으로 사용되는 Lee 상변화 모델로부터 다음과 같이 나타낼 수 있다.
| (1) |
| (2) |
여기서 은 단위시간 및 단위체적당 상변화되는 수소의 질량이며 하첨자 l, v는 수소의 액체 및 기체상을 의미한다. α, ρ, T 그리고 Tsat는 각각 체적분율, 밀도, 온도 그리고 포화온도를 의미한다. 액체수소의 기화 및 기체수소의 액화 시 열에너지가 방출 및 흡수되며 이는 다음과 같이 나타낼 수 있다.
| (3) |
S는 열에너지, H는 수소의 잠열(latent heat)을 의미하며 계산된 에 곱하면 방출 및 흡수되는 열에너지가 계산된다.
Lee 상변화 모델의 물질 전달식에서 기화 및 액화는 각 상의 포화온도에 따라 나타나며 이때 상변화되는 수소의 질량 은 경험적 계수 L에 의하여 결정된다. L은 시행착오법(trial and error method)을 통해 실험으로 측정된 결과와 유사한 결과가 도출될 때까지 수치 해석을 수행하여 얻어지는 경험적 계수이므로 다양한 형상의 저장용기 및 운용 조건에 따라 Lee 상변화 모델을 범용적으로 사용하기에는 어려움이 따른다.
2.2 분자 간 상호작용 기반 상변화 모델
Lee 상변화 모델과 같이 시행착오법을 통한 경험적 계수가 필요 없는 상변화 모델의 물질 전달식을 제안하였다. 수소 분자 간 거리의 변화에 따른 레너드-존스 퍼텐셜 에너지(Lennard-Jones potential energy) 및 런던 분산력(London dispersion force) 기반 에너지를 고려하여 기화 및 액화의 기준이 되는 에너지를 계산하고 볼츠만 분포에 적용하였다.
기화 시 경계면에서의 물질 전달식은 레너드-존스 퍼텐셜 에너지 Elv를 이용하였다. 분자 간 거리에 따른 힘의 변화를 고려하여 액체 및 기체상의 수소 분자가 갖는 에너지 εl 및 εv는 다음과 같다.
| (4) |
여기서 d0와 ε0는 각각 분자 고유 직경(hard sphere diameter) 및 수소 분자의 퍼텐셜 우물(potential well)에 해당하는 에너지로 이들의 크기는 Table 1에 나타내었다. dl과 dv는 각각 액체 및 기체수소 분자 간 거리로 각 분자의 구조가 면심입방격자라는 가정하에 충진율 0.7405와 Table 1과 같은 아보가드로 수 NA 및 수소의 분자량 MH2로부터 이를 계산할 수 있다. 따라서 기화에 필요한 레너드-존스 퍼텐셜 에너지 Elv는 기체상의 수소 분자가 갖는 에너지 εv와 액체상의 에너지 εl의 차이인 ε으로부터 다음의 식으로 나타낼 수 있다.
| (5) |
여기서 Z는 하나의 수소 분자 주위의 인접한 분자 수로 12개이다.
액체수소의 기화 여부는 포화온도인 Tsat을 기준으로 현재의 온도 T가 Tsat보다 높을 때 나타나며 이때 단위질량당 기화에 필요한 에너지인 Elv는 볼츠만 분포를 갖는 수소 분자에 대한 확률밀도함수로 표현할 수 있다. 따라서 단위시간 및 체적당 기화하는 액체수소의 질량 를 물질 전달식으로 나타내면 다음과 같다.
| (6) |
여기서 αl은 액체수소에 대한 체적분율, R은 일반 기체상수로 Table 1과 같다.
한편 액화 시 경계면에서의 물질 전달식은 런던 분산력 기반 에너지인 Evl을 이용하였다. Evl은 무극성 분자 사이에서 발생하는 인력인 런던 분산력에 대한 퍼텐셜 에너지로 다음과 같이 계산된다.
| (7) |
여기서 p와 I는 각각 분극률(polarizability)과 이온화 전위(ionization potential)로 Table 1과 같다.
기화와 유사한 방법으로 단위시간 및 단위체적당 액화하는 기체수소의 질량 을 물질 전달식으로 나타내면 다음과 같다.
| (8) |
기화와 액화 시 나타나는 분자 간 상호작용 기반 상변화 모델로 얻어지는 Elv와 Elv를 볼츠만 분포에 적용하여 확률밀도함수로 나타내면 Fig. 1과 같다. 수소의 평균온도 T와 포화온도 Tsat에 해당하는 에너지의 확률밀도함수가 각각 high 및 low temperature에 해당하는 선이라면 액체수소의 미소체적에 대한 T가 Tsat보다 크면 Elv보다 큰 에너지를 가지는 수소 분자들은 기화하며 반대의 경우 Evl보다 작은 에너지를 가지는 수소 분자들은 액화한다. 따라서 수소의 기화 과정에서는 Elv 이상의 에너지를 가지는 수소 분자가 기화하였으며 이때 Elv만큼의 에너지를 소모한다. 또한 액화 과정에서는 Evl만큼의 에너지를 방출하며 이를 수치 해석적으로 모사하기 위하여 열에너지에 대한 생성항(source term)을 적용하였다. 단위 시간 및 단위체적당 기화 시 소모하는 에너지와 액화 시 방출하는 에너지인 Slv와 Svl은 및 그리고 Elv 및 Evl로부터 다음과 같이 계산된다.
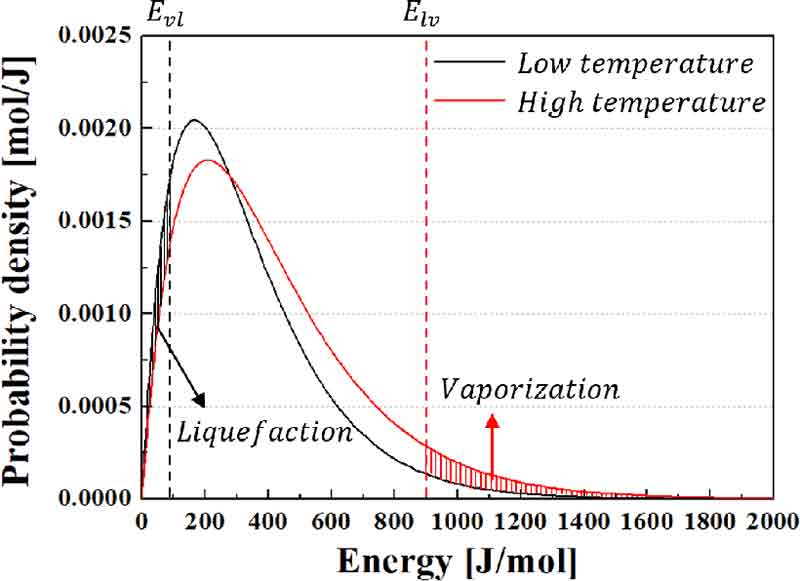
Probability density of energies for vaporization and liquefaction obtained by phase change model based on Intermolecular Interactions
| (9) |
| (10) |
3. 다상 열유동 해석
3.1 대상 및 해석 전처리
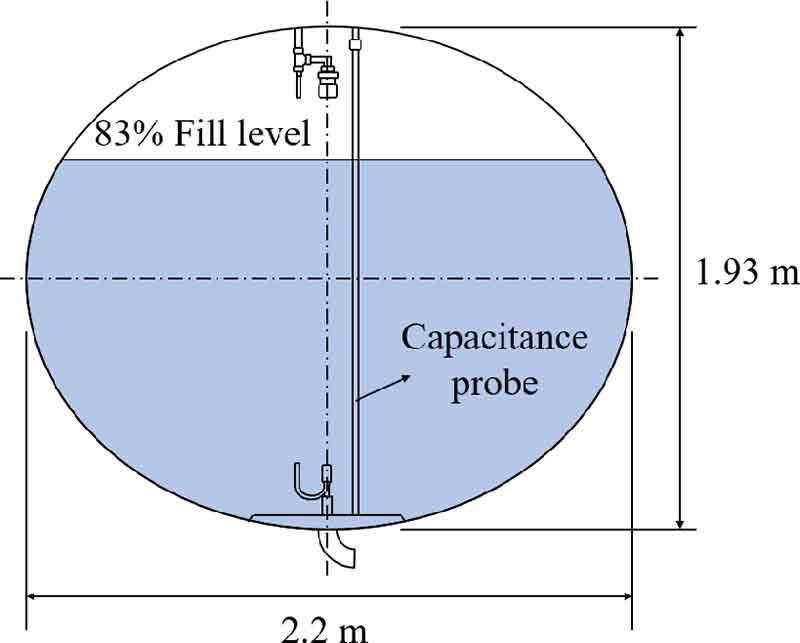
분자 간 상호작용 기반 상변화 모델을 이용하여 액체수소 저장용기에서 발생하는 BOG 발생량과 압력 상승률을 추정하기 위하여 Fig. 2와 같이 NASA Lewis Research Center의 self-pressurization 실험에 사용된 직경 2.2 m, 높이 1.93 m, 부피 4.89 m3 및 충진율 83%인 타원형 액체수소 저장용기12)를 대상으로 다상 열유동 해석을 수행하였다.
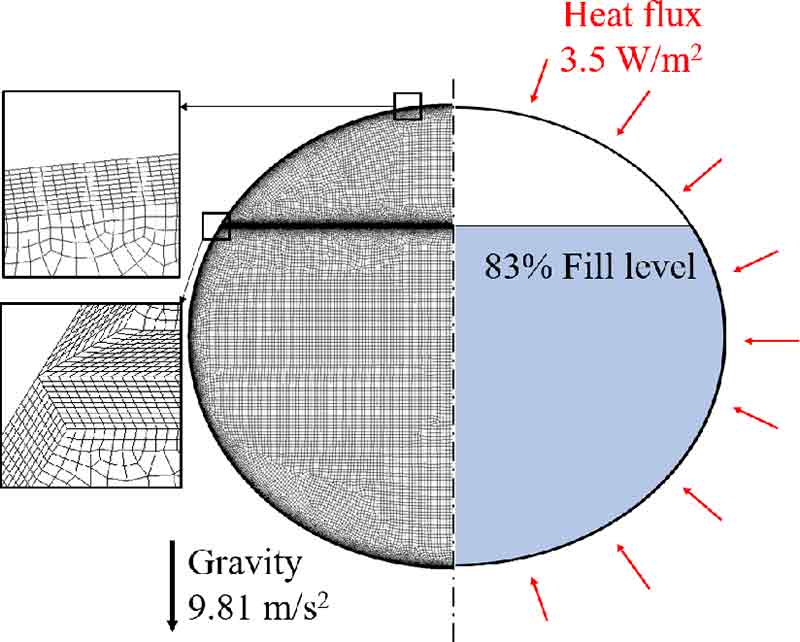
해석에 요구되는 과도한 시간을 절감하기 위하여 2D 축대칭 모델을 사용하였다13-15). 저장용기를 지지하는 외부 구조물 및 센서 설치를 위한 내부 구조물은 해석 대상에서 제외되었다. Fig. 3은 다상 열유동 해석을 위한 격자의 생성과 하중, 경계 조건으로 벽면의 격자 크기는 1 mm이며 0.5 mm 간격으로 10층의 inflation 조건을 적용하여 생성된 격자는 총 86,866개의 사각형 격자(quadrilateral element)로 구성되었다. 해당 격자는 39,366, 61,982, 86,866개의 격자 수준에 대한 격자 의존성 테스트를 활용하여 도출되었다. 압력 상승률 및 BOG 발생량을 검토하였으며 61,982개 및 86,866개의 격자 수준에서 비슷한 결과가 나타남을 확인하였다.
3.2 해석 방법
분자 간 상호작용 기반 상변화 모델에 의한 액체 및 기체수소의 기화와 액화를 모사하기 위하여 ANSYS Fluent (Ansys, Canonsburg, PA, USA)의 user defined function (UDF)을 사용하였으며 UDF를 포함한 해석 순서는 Fig. 4에 나타내었다. 단위시간 및 체적당 상변화하는 수소의 질량은 DEFINE_MASS_TRANSFER 명령어를 사용하였으며 상변화 시 소모 및 방출하는 에너지는 DEFINE_SOURCE 명령어를 적용하여 계산하였다. 작동유체인 수소의 물성치는 미국 국립표준기술연구소(National Institute of Standards and Technology, NIST)의 normal-수소에 대한 자료16)를 기반으로 밀도(density), 열전도도(thermal conductivity), 점도(viscosity), 표면장력(surface tension) 등을 압력 및 온도에 관한 수식으로 변환하여 적용하였다. 수소는 양성자의 스핀 방향과 이에 따른 각운동량에 의하여 ortho-수소와 para-수소의 분자 형태를 가지며17) normal-수소와 para-수소의 물성은 약간의 차이를 보인다. Normal-수소는 para-수소와 ortho-수소가 1:3의 비율로 혼합되어 있으며 액체수소는 para-수소와 ortho-수소가 99.8:0.2의 비율로 혼합되어 있다. 조성비 차이에 의해 물성의 차이가 발생하지만 101,325 Pa 및 15-25 K 조건에서 밀도 및 비열에 대한 오차율을 계산하면 각각 최대 0.19% 및 0.93%의 작은 차이를 보인다.
하중 및 경계 조건으로 저장용기의 모든 벽면에 대하여 self-pressurization 실험12)과 동일하게 Table 2와 같이 열유입(heat flux) 3.5 W/m2, 중력가속도 9.81 m/s2, 초기압력 101,323 Pa 그리고 온도 20.369 K를 부과하였다.
액체-기체 계면은 volume of fraction (VOF) 방법으로 모사하였으며 이때 압력 기반 해석법(pressure-based solver)과 semi-implicit method for pressure linked equations-consistent (SIMPLEC) 알고리즘을 적용하였다18-20). 압력 구배와 액체-기체 계면의 계산을 위하여 ANSYS Fluent의 body-force-weighted 및 geo-reconstruct scheme을 이용하였다. 이를 통해 부력 및 자연대류를 고려한 계면에서의 압력을 구하였고 액체-기체 계면을 선명하게 모사할 수 있었다.
한편 벽 근처에서 나타나는 유동의 정확한 계산을 위하여 realizable k-ε 난류 모델과 y+ 값 30 이하에서 사용되는 enhanced wall function이 적용되었으며 본 연구에서의 최대 y+는 20.1로 30 이하를 만족한다. 또한 질량 손실에 의한 오차를 최소화하기 위하여 Courant number 0.1 이하를 만족하는 시간 간격을 사례 분석을 통해 도출하였다. 0.010, 0.005 그리고 0.001초의 시간 간격에 대하여 30초간 해석을 수행하였고 수소의 총 질량을 검토하였다. 시간 간격에 따른 질량 손실 결과를 Table 3에 정리하였으며 Courant number가 높은 경우 질량이 보존되지 않음을 확인하였다. 따라서 질량이 보존되는 0.001초의 시간 간격을 사용하여 30초 동안 과도 해석을 수행하였다21).
4. 해석 결과 및 고찰
4.1 해석 결과
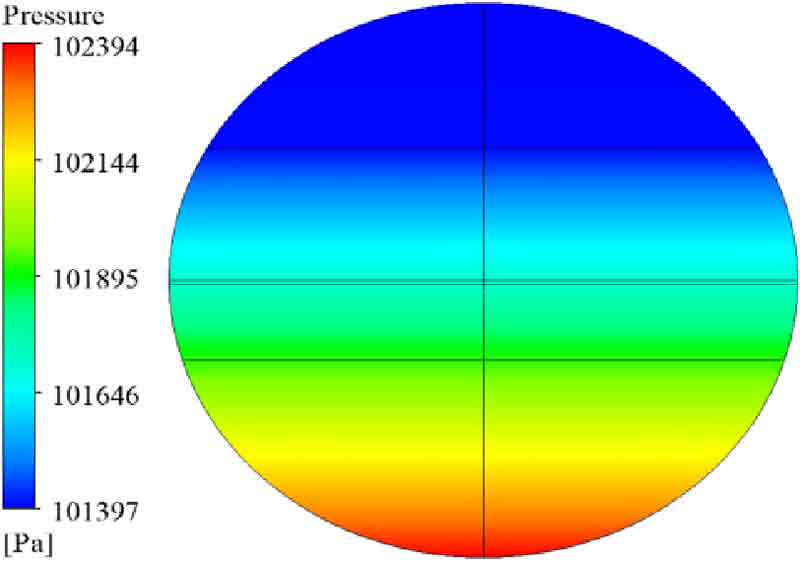
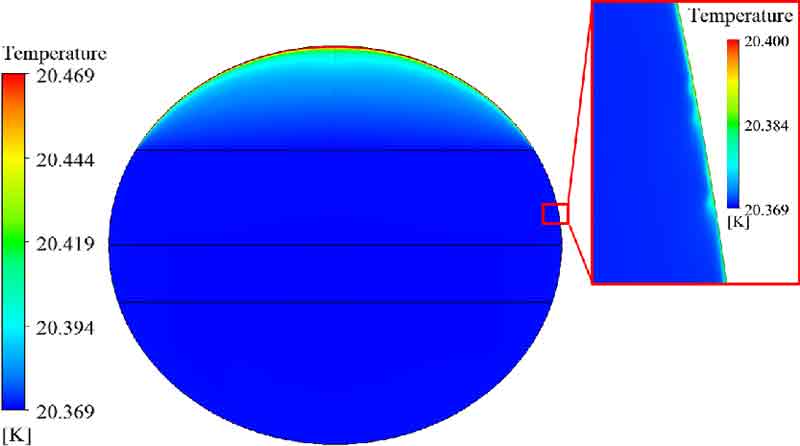
Fig. 5는 다상 열유동 해석이 종료된 30초에서 저장용기 내의 압력 분포이다. 평균 압력은 101,743 Pa이며 액체수소의 상대적으로 높은 밀도와 중력의 작용으로 저장용기의 바닥 방향으로 압력이 증가하여 바닥면에서 102,394 Pa의 최대 압력이 작용하였다. 바닥면에서의 높은 압력은 포화온도 상승의 원인이되어 BOG의 발생을 억제한다.
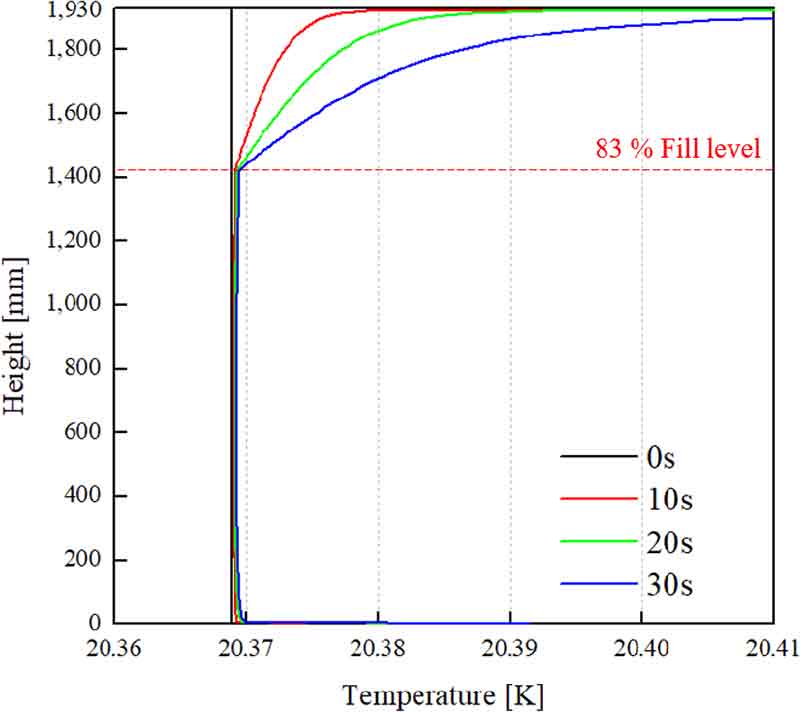
Fig. 6은 과도 해석의 시간인 0, 10, 20 및 30초에서 저장용기 높이에 따른 온도의 변화를 보여주고 있다. 충진율 83%에 해당하는 높이 상부의 기체수소의 온도가 시간의 경과에 따라 증가하는 경향을 보였다. 또한 액체수소 영역에서 높이 600 mm를 기준으로 위 또는 아래로 갈수록 온도가 높아지는 경향이 나타난다. 상부로 갈수록 온도가 높아지는 이유는 시간이 흐름에 따라 열적 성층(thermal stratification)이 형성되기 때문이며 하부로 갈수록 온도가 높아지는 이유는 벽면으로 열에너지가 유입되었기 때문이다.
Fig. 7은 다상 열유동 해석이 종료된 30초에서 압력용기 내의 온도 분포이다. 기체-액체 계면을 기점으로 기체수소 영역에서 뚜렷한 온도구배와 성층(stratification)이 형성되고 있다. 기체수소의 온도는 액체수소 대비 적은 열용량으로 빠르게 올라가고 기체수소는 저장용기의 상부로 상승하여 21.08 K의 최대 온도에 도달한다. 한편 액체수소와 접하는 저장용기 내벽에는 열 경계층(thermal boundary layer)이 국소적으로 불규칙하게 형성되었다. 이는 내벽 벽면에서 국소적으로 발생한 미량의 BOG 때문으로, BOG 발생이 포함된 영역을 따라 높은 온도 영역이 형성되었다. 벽면으로부터의 열유입에 의해 BOG는 가열되고 밀도 차이로 인해 상승하여 저장용기 상부에 도달한다.
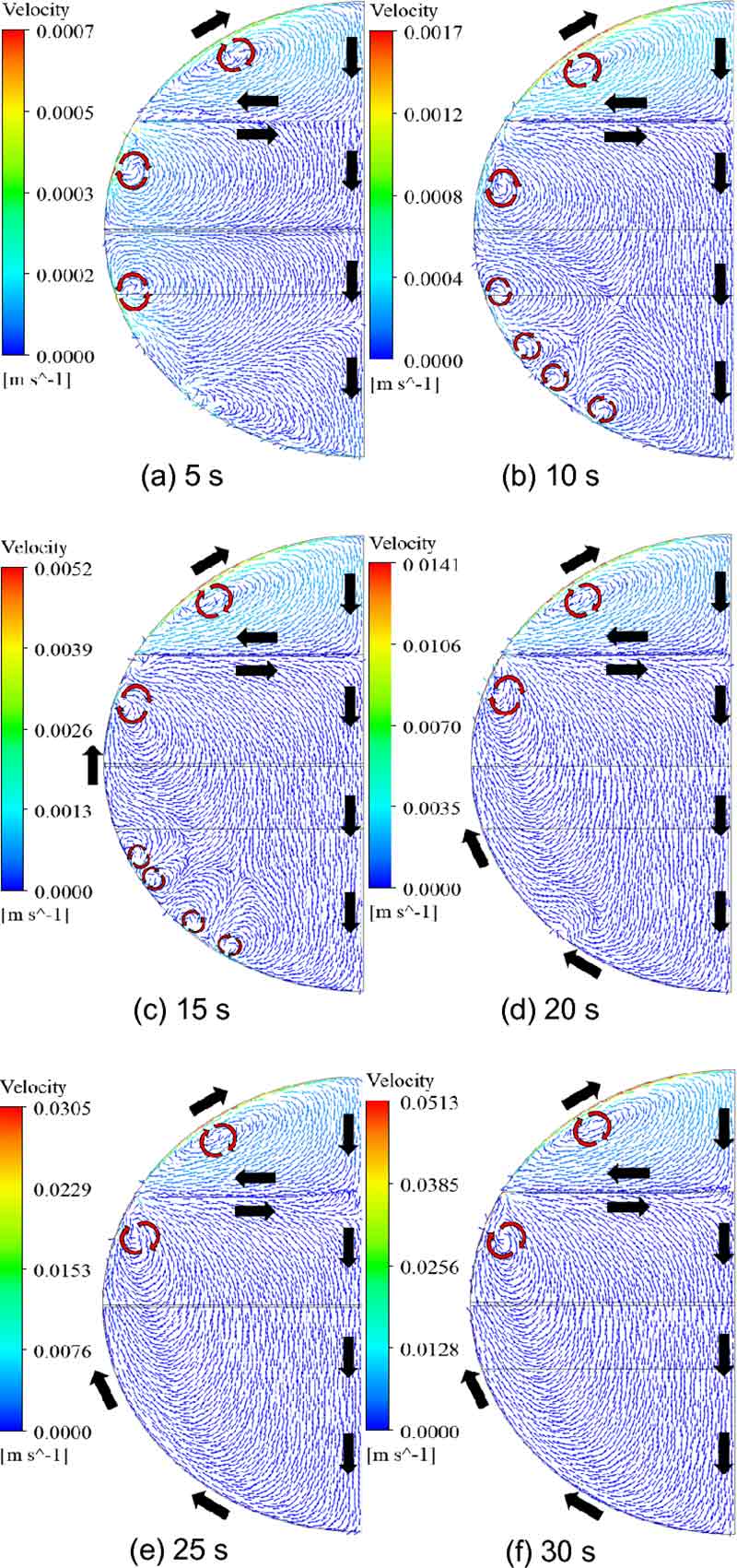
Fig. 8은 다상 열유동 해석으로부터 얻어진 30초 동안의 속도장 변화를 나타낸 것이다. 5초 간격으로 나타냈으며 액체 및 기체수소의 유동을 화살표로 표기하였다. 모든 영역에서 유체의 속도가 0 m/s로 유동이 없는 초기 조건이 적용되었으며 벽면을 통해 유입되는 열에너지로 인해 벽면 근처 수소는 온도가 상승하고 밀도가 감소하여 상승하는 경향을 보인다.
기체-액체 계면에서는 서로 반대 방향의 속도장이 나타났으며 기체수소 영역에서는 벽면으로부터의 열유입으로 가열된 기체수소가 상부로 상승하고 상부에 머물러 있던 기체수소는 밀려나 중심을 따라 하강한다. 또한 하강하는 기체수소는 상대적으로 온도가 낮은 주변 기체수소에 의해 냉각되며 기체-액체 계면에 도달한 후 미량의 기체수소가 재액화(re-liquefaction)된다. 온도 및 밀도 차이로 인하여 벽면, 중심선, 기체-액체 계면을 따라 순환하는 유동장이 형성됨을 알 수 있다.
한편 액체수소 영역에서 해석 시작 후 15초까지는 Fig. 8(a)-(c)와 같이 상대적으로 높은 온도를 가지는 벽면 근처의 수소와 낮은 온도를 가지는 중심선 근처의 수소가 혼합하여 국소적인 와류가 발생하였다. 15초 이후 Fig. 8(d)-(f)와 같이 저장탱크 하부 벽면의 와류가 사라지기 시작하였으며 액체 및 기체수소 영역에 각각 하나의 큰 와류만 남고 유동이 안정되었다. 또한 벽면을 따라 상승하여 계면에 도달한 액체수소는 주변의 낮은 온도를 가지는 액체수소 및 기체수소와 열적 평형을 이루었다. 이후 벽면 방향 또는 기체수소의 영역으로는 이동할 수 없으므로 계면을 따라 저장용기 중심으로 이동한 후 하강하였다.
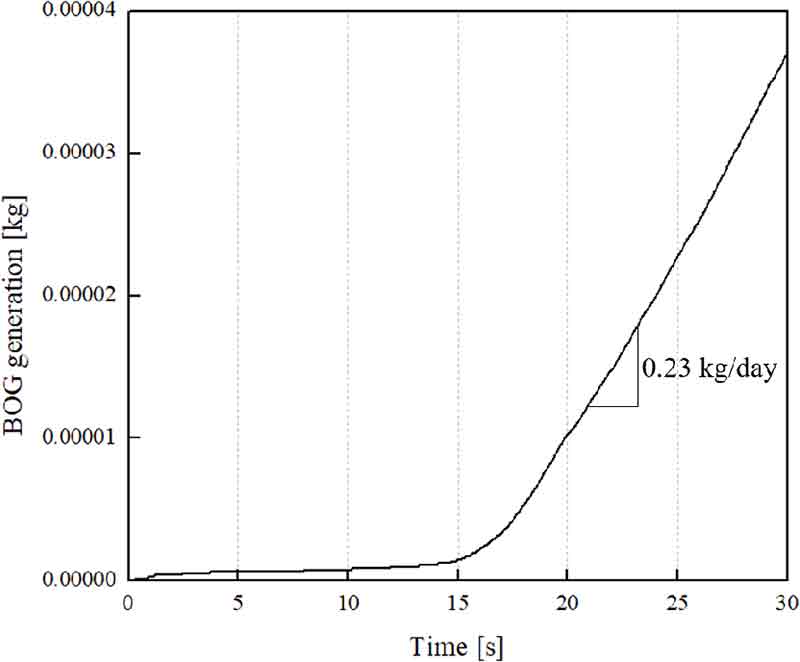
Fig. 9는 다상 열유동 해석으로부터 얻어진 30초 동안의 BOG 발생량의 변화이다. 약 15초 이전에는 기화율이 상대적으로 낮으며 이는 열유입으로 인하여 형성된 와류에서 기인한다. 와류는 벽면 근처의 높은 온도를 가지는 액체수소와 중심선 근처의 낮은 온도를 가지는 액체수소의 열교환을 촉진시켜 벽면 근처의 액체수소의 온도 상승을 더디게 하여 기화 억제의 원인이 된다. 15초 이후 와류가 점차 사라지기 시작하며 20초 이후에는 유동이 안정되어 0.23 kg/day의 BOG 발생률이 나타났다. 이를 액체수소 질량을 고려하여 백분율로 환산하면 0.08%/day 수준이다.
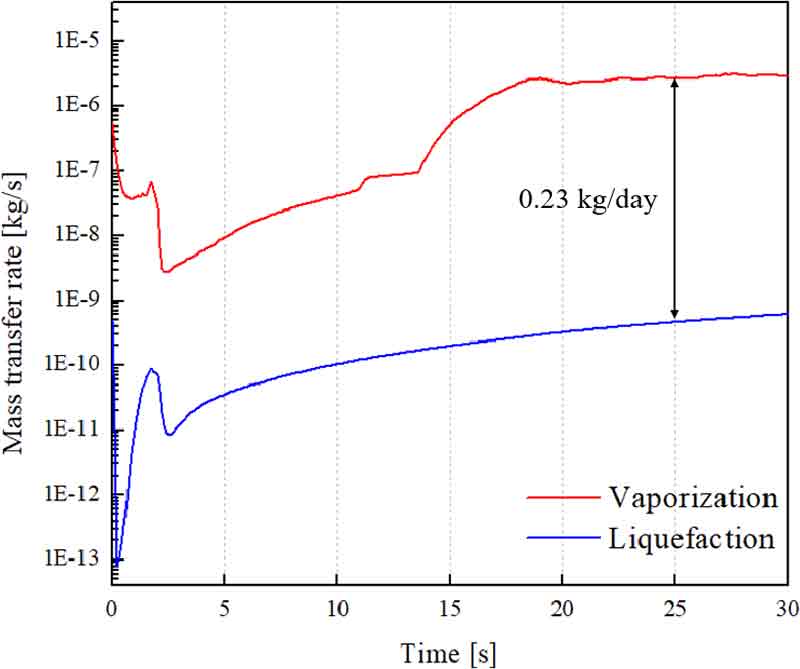
Fig. 10은 식 (6)과 (8)로 계산된 단위시간 및 단위 체적당 기화 및 액화하는 수소의 질량 및 을 체적 적분한 것으로 이를 로그 스케일로 나타내었다. 해석 초기의 약 3초간 불안정한 변화를 보였으나 수소의 온도가 상승함에 따라 밀도가 변화하고 상승 및 하강하는 유동과 와류가 형성되며 약 14초까지 및 이 조금씩 상승하였다. 이후 약 14초에서 18초 동안 가 급격히 상승하였는데 이는 앞 문단에서 설명한 것과 같이 벽면 근처의 액체수소의 온도 상승을 더디게 하는 와류가 사라졌기 때문이다. 20초 이후 유동이 안정되었으며 에서 을 빼서 저장용기 내의 BOG 발생률을 계산하였다. 25초에서 계산된 BOG 발생률은 0.23 kg/day로 Fig. 8에서 계산한 값과 일치함을 확인하였다.
4.2 고찰
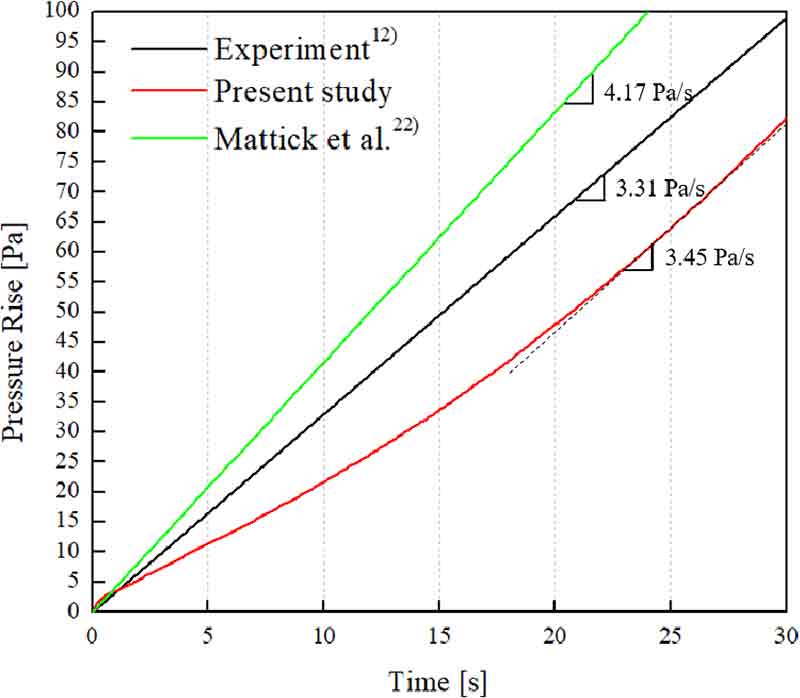
Fig. 11은 분자 간 상호작용 기반 상변화 모델을 사용한 다상 열유동 해석으로 얻어진 압력용기 내의 압력 변화이다. 과도 해석이 이루어진 30초 동안 외부로부터의 열 유입으로 기체수소의 온도가 상승하고 BOG가 발생하여 압력이 증가하였다. 해석으로 얻어진 30초 동안의 압력 상승률은 2.7 Pa/s로 NASA Lewis Research Center의 self-pressurization 실험에서 얻어진 결과인 3.31 Pa/s보다 낮으나 20초 이후의 압력 상승률은 3.45 Pa/s로 실험 결과와 약 4.2%의 오차를 보였다. 한편 동일한 압력용기에 Mattick 등22)이 제안한 multi-node lumped parameter model을 해석 결과와 비교하였다. 압력 상승률은 4.17 Pa/s로 실험 결과와 약 26.0%의 오차를 보였다. 그러나 Mattick 등22)은 6시간 이상 해석을 수행하였으며 이때 압력 상승률의 오차는 6.5%로 감소하였다.
분자 간 상호작용 기반 상변화 모델을 사용하여 도출한 30초 동안의 결과는 비교적 정확하게 실험 결과를 모사하고 있다. 따라서 액체수소 저장용기 설계 및 실험에 앞서 해석을 통한 압력 상승 및 BOG 발생에 대한 경향을 파악할 수 있을 것으로 사료된다. 그러나 분자 간 상호작용 기반 상변화 모델은 경험적 계수가 요구되지 않는다는 장점이 있으나 볼츠만 분포를 만족하지 않는 분자를 대상으로는 정확한 예측이 어려운 한계가 있다. 또한 수치적 안정성을 확보하기 위해서 작은 시간 간격을 사용하여 과도한 계산 시간이 요구되며 장시간의 해석 수행에 어려움이 있다. 추후 수치 해석 방법의 개선을 통해 장시간 동안의 BOG 발생 거동을 확인할 예정이다.
5. 결 론
본 연구에서는 경험적 계수가 요구되지 않는 분자 간 상호작용 기반 상변화 모델을 제안하여 NASA Lewis Research Center의 self-pressurization 실험에서 사용된 타원형 액체수소 저장용기를 대상으로 압력 상승률과 BOG 발생률 그리고 저장용기 내의 유동 특성을 분석하였다.
- 1) 레너드-존스 퍼텐셜 에너지 및 런던 분산력에 대한 에너지를 볼츠만 분포에 적용하여 분자 간 상호작용 기반 상변화 모델을 제안하였다.
- 2) 83%의 액체수소가 충전된 타원형 저장용기에 대해 101,323 Pa 및 20.369 K의 내부 압력과 온도를 초기 조건으로 하고 모든 벽면에 3.5 W/m2의 열유속을 부과하여 30초 동안의 다상 열유동 해석을 수행하였다. 해석 시작으로부터 약 20초 이후 3.45 Pa/s의 압력 상승률이 계산되었으며 NASA Lewis Research Center의 실험으로부터 얻어진 압력 상승률인 3.31 Pa/s와 유사함을 확인하였다.
- 3) 저장용기의 내벽 벽면에서는 열 경계층이 형성되며 기체 및 액체수소는 상승하고 중심에서는 하강하는 유동을 보였으며 액체수소 영역의 내벽 벽면에서 국소적인 와류가 형성되었다. 저장용기 하부에서는 정수압으로 인해 압력이 높게 형성되어 기화가 억제되었으며 계면에서는 하강한 기체수소가 냉각되며 아주 적은 양이 액화되었다.
- 4) 다상 열유동 해석으로 얻어진 BOG 발생률은 0.23 kg/day이며 분자 간 상호작용 기반 상변화 모델의 단위 시간당 기화 및 액화하는 수소 질량의 차로 계산한 BOG 발생률과 일치하였다.
- 5) 본 연구에서 제안한 상변화 모델을 이용하여 현실적으로 실험이 어려운 액체수소 저장용기 모델과 다양한 외부 환경에 대한 다상 열유동 해석이 가능하며 얻어진 결과를 초기 설계의 참고 자료로 활용할 수 있을 것으로 사료된다.
Acknowledgments
본 논문은 부산광역시 및 (재)부산테크노파크의 BB21 plus 사업으로 지원된 연구임.
References
-
S. J. Oh, K. S. Jeon, J. H. Yoon, and J. Choi, “A study on the thermal characteristics of the vacuum jacket valve for transporting liquefied hydrogen according to the degree of vacuum”, Journal of Hydrogen and New Energy, Vol. 32, No. 6, 2021, pp. 585-591.
[https://doi.org/10.7316/KHNES.2021.32.6.585]

-
S. Park, C. Lee, J. Ryu, and S. Hwang, “An economic analysis on slush hydrogen containing liquid and solid phase for long-term and large-scale storage”, Journal of Hydrogen and New Energy, Vol. 33, No. 3, 2022, pp. 247-254.
[https://doi.org/10.7316/KHNES.2022.33.3.247]

-
M. Choi, W. Jung, S. Lee, T. Joung, and D. Chang, “Thermal efficiency and economics of a boil-off hydrogen re-liquefaction system considering the energy efficiency design index for liquid hydrogen carriers”, Energies, Vol. 14, No. 15, 2021, pp. 4566.
[https://doi.org/10.3390/en14154566]

-
C. Chae, G. Im, Y. Kim, and S. Chae, “An analysis of the impact of design factors using a simulator of LH2 storage tank PRV system”, Journal of the Korean Institute of Gas, Vol. 28, No. 2, 2024, pp. 47-55.
[https://doi.org/10.7842/kigas.2024.28.2.47]

-
J. Fu, B. Sunden, and X. Chen, “Analysis of self-pressurization phenomenon in a cryogenic fluid storage tank with VOF method”, In: ASME 2013 International Mechanical Engineering Congress and Exposition; 2013 Nov 15-21; San Diego (CA), USA. New York (NY): American Society of Mechanical Engineers, c2013, pp. V001T01A020.
[https://doi.org/10.1115/IMECE2013-63209]

- W. H. Lee, “Pressure iteration scheme for two-phase flow modeling“, Multiphase Transport : Fundamentals, Reactor Safety, Applications, Vol. 1, pp. 407-431. Retrieved from https://codethatflows.wordpress.com/wp-content/uploads/2021/08/406441216-lee-model-pdf-1.pdf, .
-
G. Wei and J. Zhang, “Numerical study of the filling process of a liquid hydrogen storage tank under different sloshing conditions”, Processes, Vol. 8, No. 9, 2020, pp. 1020.
[https://doi.org/10.3390/pr8091020]

-
G. M. Jeon, J. C. Park, and S. Choi, “Multiphase-thermal simulation on BOG/BOR estimation due to phase change in cryogenic liquid storage tanks”, Applied Thermal Engineering, Vol. 184, 2021, pp. 116264.
[https://doi.org/10.1016/j.applthermaleng.2020.116264]

-
M. Ahammad, T. Olewski, L. N. Véchot, and S. Mannan, “A CFD based model to predict film boiling heat transfer of cryogenic liquids”, Journal of Loss Prevention in the Process Industries, Vol. 44, 2016, pp. 247-254.
[https://doi.org/10.1016/j.jlp.2016.09.017]

-
P. J. Berenson, “Film-boiling heat transfer from a horizontal surface”, ASME Journal of Heat and Mass Transfer, Vol. 83, No. 3, 1961, pp. 351-356.
[https://doi.org/10.1115/1.3682280]

-
V. V. Klimenko, “Film boiling on a horizontal plate - new correlation”, International Journal of Heat and Mass Transfer, Vol. 24, No. 1, 1981, pp. 69-79.
[https://doi.org/10.1016/0017-9310(81)90094-6]

- M. M. Husan, C. S. Lin, and N. T. Vandresar, “Self-pressurization of a flightweight liquid hydrogen storage tank subjected to low heat flux”, In: 1991 ASME/AIChE National Heat Transfer Conference; 1991 Jul 28-31; Minneapolis (MN), USA. Cleveland (OH): NASA Lewis Research Center, c1991. Retrieved from https://ntrs.nasa.gov/citations/19910011011, .
-
T. Perrotin and D. Clodic, “Thermal-hydraulic CFD study in louvered fin-and-flat-tube heat exchangers”, International Journal of Refrigeration, Vol. 27, No. 4, 2004, pp. 422-432.
[https://doi.org/10.1016/j.ijrefrig.2003.11.005]

-
M. J. Huang, P. C. Eames, and B. Norton, “Comparison of a small-scale 3D PCM thermal control model with a validated 2D PCM thermal control model”, Solar Energy Materials and Solar Cells, Vol. 90, No. 13, 2006, pp. 1961-1972.
[https://doi.org/10.1016/j.solmat.2006.02.001]

- M. A. Salehi and R. Rahimi, “Comparison between 2D and 3D transient flow simulation of gas liquid dynamics in two-phase cylindrical bubble column reactors by CFD”, International Journal of Chemical Sciences, Vol. 6, No. 2, 2008, pp. 857-872. Retrieved from https://www.tsijournals.com/articles/comparison-between-2d-and-3d-transient-flow-simulation-of-gas--liquid-dynamics-in-twophase-cylindrical-bubble-column-rea.pdf, .
-
National Institute of Standards and Technology (NIST), “NIST Chemistry WebBook: NIST standard reference database number 69”, NIST, 2023.
[https://doi.org/10.18434/T4D303]

- H. Y. Lim and I. H. Cho, “Characteristics of hydrogen and considerations as a rocket propellant”, Proceedings of the Korean Society of Propulsion Engineers Conference, Vol. 2009, No. 11a, 2009, pp. 23-26. Retrieved from https://koreascience.or.kr/article/CFKO200911764903027.page, .
-
C. W. Hirt and B. D. Nichols, “Volume of fluid (VOF) method for the dynamics of free boundaries”, Journal of Computational Physics, Vol. 39, No. 1, 1981, pp. 201-225.
[https://doi.org/10.1016/0021-9991(81)90145-5]

-
J. U. Brackbill, D. B. Kothe, and C. Zemach, “A continuum method for modeling surface tension”, Journal of Computational Physics, Vol. 100, No. 2, 1992, pp. 335-354.
[https://doi.org/10.1016/0021-9991(92)90240-Y]

-
M. Kassemi and O. Kartuzova, “Effect of interfacial turbulence and accommodation coefficient on CFD predictions of pressurization and pressure control in cryogenic storage tank”, Cryogenics, Vol. 74, 2016, pp. 138-153.
[https://doi.org/10.1016/j.cryogenics.2015.10.018]

-
B. Sundén and J. Fu, “Heat transfer in aerospace applications”, Academic Press, USA, 2017, pp. 71-87.
[https://doi.org/10.1016/B978-0-12-809760-1.00005-3]

-
S. Mattick, C. Lee, A. Hosangadi, and V. Ahuja, “Progress in modeling pressurization in propellant tanks”, In: 46th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit; 2010 Jul 25-28; Nashville (TN), USA. Reston (VA): American Institute of Aeronautics and Astronautics; c2010, pp. 1-12.
[https://doi.org/10.2514/6.2010-6560]