수소 충전용 리셉터클에서 작동유체인 수소와 불활성 기체 간 차압 상사성에 관한 수치적 연구

1. 서 론

기후 변화에 대비하여 전 세계 각국에서 기후 협약을 맺고 저탄소 배출을 목표로 친환경 에너지 개발을 위해 노력하고 있다. 국내에서도 탄소중립을 목표로 친환경 에너지 개발에 힘쓰고 있으며 그 일환 중 하나로 수소 전기 자동차 개발 및 상용화를 위한 연구가 활발히 진행 중이다.

수소 전기차 충전에는 레귤레이터나 리셉터클과 같은 다양한 요소 부품이 필요하다. 수소 충전 시간을 단축하고 저온의 수소를 안정적으로 공급하기 위해 저온 및 고압에서 부품의 내구성이 확보되어야 한다. 부품의 성능 향상 개발을 위해 차압 분석이 필요하나 작동유체가 수소일 경우 누출 시 폭발 및 화재의 위험이 있고 관리와 보관이 어려운 문제가 있다. 실제로 수소의 폭발 위험성을 논하는 연구도 오랜 기간 동안 진행되었다^1,2). 개발 단계에서 실제 유체로 각 부품의 유동 실험을 진행하기에는 위험성이 있으므로 상온, 상압에서 폭발 위험성이 낮은 불활성 기체를 이용한 대체 실험 방안이 필요하다.

한편 위험성이 높은 유체의 실험을 대체하여 수치해석을 통한 성능 평가를 고려할 수 있다. 수소 충전 시스템과 관련한 해석 연구로 Kwon 등³⁾은 수소 밸브의 유체 온도 변화에 따른 유속 변화와 밀도 변화의 관계를 파악하였고 Oh와 Suh⁴⁾는 부품인 체크밸브의 고압, 저온 조건에서 유동 특성을 분석하였다. Baek 등⁵⁾은 수소 충전 노즐의 유동 해석을 이용하여 설계의 타당성을 검증하였고 Park 등⁶⁾은 충전기용 압축기 벨로우즈의 형상 설계에서 성능과 안정성을 향상시키기 위한 중요 인자 파악 연구를 진행하였다. 또한 Wang 등⁷⁾은 고 해석을 통해 부품 내부 압력 분포를 파악하였다. 수소 부품과 관련해 유동을 파악하는 여러 해석 및 연구들이 진행되었지만 차압 분석 및 실험을 위한 수소와 불활성 기체 간의 상관성 정보는 부족하다.

본 연구에서는 리셉터클 성능 인자 중 하나인 차압을 수치해석적 연구를 통해 계산하였다. 특히 리셉터클이 실제 작동하는 저온, 고압 환경에서 화재 및 폭발의 위험성이 큰 수소를 활용한 실험을 대체할 수 있는 방안을 모색하고자 수소와 불활성 기체 간 상관관계를 분석하였다. 리셉터클에서 수소와 불활성 기체를 이용한 내부 유동 분석과 차압에 미치는 인자를 확인하였고 불활성 기체를 이용하여 수소의 차압 결과를 예측할 수 있는 상관식을 도출하였다.

2. 연구 방법

2.1 실험

2.1.1 실험 장치 및 방법

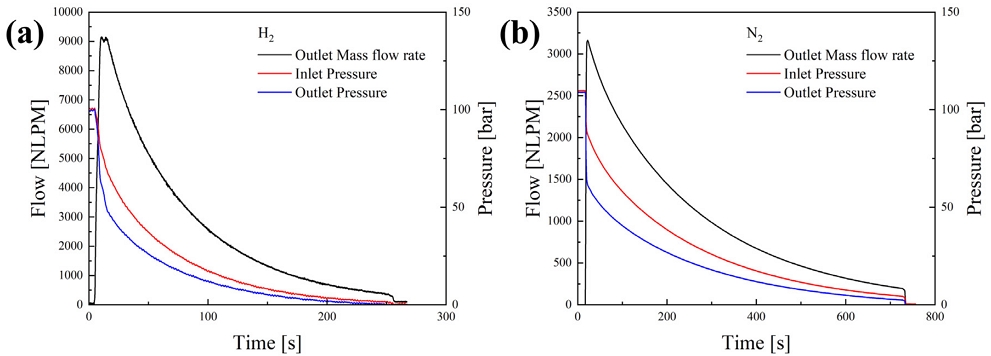
Fig. 1은 실험 장치의 개략도를 나타내었으며 상단에서부터 가스 탱크, 레귤레이터, 압력 센서, 리셉터클, 압력 센서, 유량계 순으로 구성되어 있다.

Fig. 1.

Schematic diagram of the experimental setup

리셉터클을 지났을 때의 차압을 확인하기 위한 실험으로 충분히 가압된 가스를 흘려보내며 시간에 따른 입구와 출구의 압력 및 유량을 기록하였다. 수소와 질소 초기 압력은 100 bar로 동일하다. 실험은 상온, 상압 환경에서 진행되었으며 실험에 사용된 모든 배관 및 밸브는 단열 마감 처리되지 않은 상태에서 사용되었다. 레귤레이터를 이용하여 설정된 압력에서 기체 주입 시작 후 온전히 빠져나간 뒤 실험을 종료하였다.

2.1.2 실험 결과

Fig. 2(a)는 수소, Fig. 2(b)는 질소의 압력 및 유량 측정 결과를 시간에 따른 결과로 보여 주고 있다. 초기 압력을 동일하게 설정하였음에도 초기 유량은 수소가 질소의 약 3배 정도로 나타났다. 이는 분자량 및 밀도의 차이에 의한 것으로 판단된다.

Fig. 2.

Experimental raw data. (a) Hydrogen. (b) Nitrogen

2.2 수치해석

2.2.1 수치해석 모델 및 경계 조건

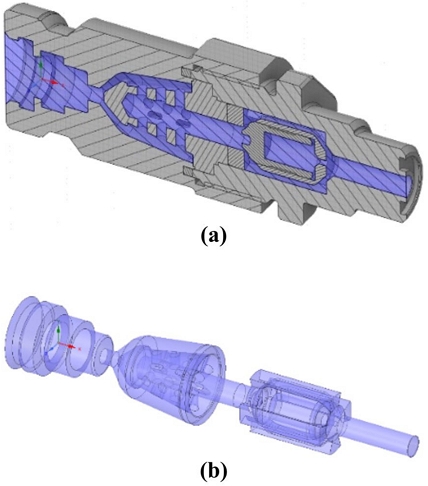
리셉터클 내부 형상은 Fig. 3과 같이 filter와 체크밸브가 축 방향으로 연결된 구조로 되어 있다. 수치해석을 위해 체크밸브는 완전히 개방한 상태로 가정하여 내부 유로인 Fig. 3(b)와 같은 형상으로 도메인을 구성하였다.

Fig. 3.

Receptacle 3-D modeling. (a) Geometry, (b) fluid part

본 해석 연구에서 3차원 비압축성, 정상 상태의 난류 유동으로 단열 상태를 가정하여 사용된 시간 평균 연속 방정식, 운동량 방정식, 에너지 방정식, 상태 방정식은 각각 식 (1)-(4)와 같다.

$\[ \frac{\partial \rho }{\partial t}+\nabla \cdot \left(\rho \overrightarrow{v}\right)=0 \]$

(1)

$\[ \begin{array}{c}\frac{\partial }{\partial t}\left(\rho \overrightarrow{v}\right)+\nabla \cdot \left(\rho \overrightarrow{v}\overrightarrow{v}\right)\hfill \\ =-\nabla p+\nabla \cdot \left(\overline{\stackrel{-}{\tau }}\right)+\rho \overrightarrow{g}+\overrightarrow{F}\hfill \end{array} \]$

(2)

$\[ \begin{array}{c}\frac{\partial }{\partial t}\left(\rho E\right)+\nabla \cdot \left(\overrightarrow{v}\left(\rho E+p\right)\right)\hfill \\ =\nabla \cdot \left(k_{eff}\nabla T-\sum _j{h}_j{\overrightarrow{J}}_j+\left({\overline{\stackrel{-}{\tau }}}_{eff}\cdot \overrightarrow{v}\right)\right)+S_h\hfill \end{array} \]$

(3)

$\[ P=\frac{RT}{V-b+c}-\frac{\alpha }{\left(V^2+\delta V+ϵ\right)} \]$

(4)

상용 코드인 ANSYS fluent 2022R2 (ANSYS, Canonsburg, PA, USA)를 해석에 사용하였으며 식 (3)의 난류 성분을 분석은 realizble k-ε 모델을 사용하였다. Wall function은 standard wall function을 사용하였으며 격자 생성을 위해 fluent meshing으로 polyhedra grid 격자로 구성하였다.

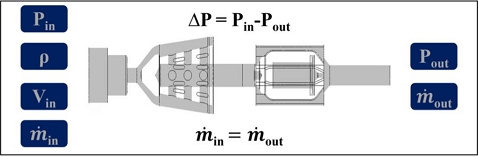
기준이 되는 유동 입구 경계 조건은 700 bar 압력에 -40℃ 온도 조건을 부여하였다. 출구는 질량 유량 조건으로 52.5 g/s로 설정하였으며 해당 조건은 리셉터클 개발 목표 유량 조건 및 실제 작동 조건과 동일하다. 다양한 작동 조건에서 현상을 분석하기 위하여 해석 변수와 case를 선정하여 Fig. 4와 Table 1에 나타내었다. 입구 압력, 밀도, 속도, 유량을 변경하며 기체에 따라 각각 9번의 수치해석을 진행하였다. 기체의 물성치를 반영하기 위해 밀도는 real gas Soave-Redlich-Kwong⁸⁾, 정압비열은 NASA 9 piecewise polynomial⁹⁾, thermal conductivity와 viscosity는 polynomial을 적용하였다.

Fig. 4.

Parameters for numerical analysis

Table 1.

Number of cases for numerical analysis

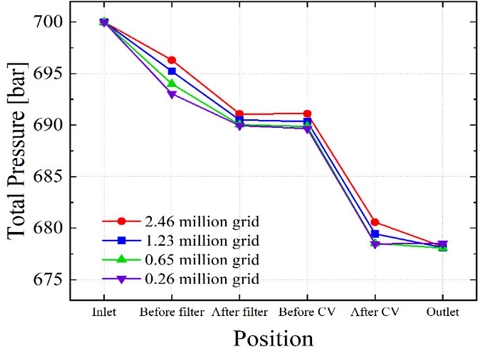
수치해석 결과의 격자 의존도를 줄이기 위해 Fig. 5와 같이 위치별 total pressure의 크기를 비교하며 격자 테스트를 수행하였다. 격자수 감소에 따라 리셉터클 내부 위치별 압력의 크기에서 약간의 차이를 보이지만 격자수가 26만 개 이상일 경우 입구와 출구 압력의 계산 결과 차이가 없음을 확인하였다. 본 연구는 리셉터클 차압의 기체 간 상사성의 확인을 목적으로 총 격자수가 26만 개로 진행할 경우 충분히 합당한 결과를 얻을 수 있다고 판단하였다.

Fig. 5.

Grid independence result based on pressure drop

2.2.2 수치해석 검증

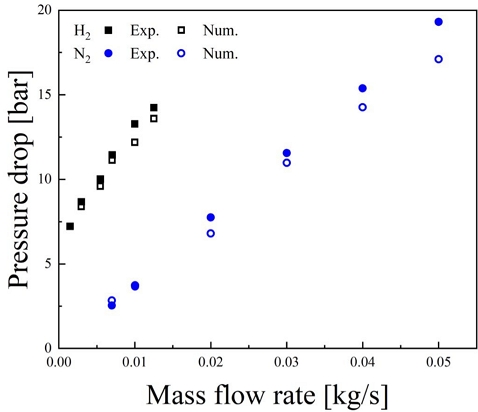
수립된 수치해석 모델을 검증하기 위해 실험 조건과 동일한 경계 조건을 부여하여 해석을 수행하였다.

시간에 따른 압력, 유량으로 측정된 결과를 각 시간별 정상 상태로 가정하여 경계 조건을 수립하였고 기체별로 각각 6번의 해석을 진행하였다. 비교 결과는 Fig. 6에서 확인할 수 있다. 실험 결과와 수치해석 간 차이는 수소는 평균 4.6%, 질소는 평균 7.6% 오차를 보인다.

Fig. 6.

Validation of numerical analysis results based on experimental data

해석으로 계산된 차압이 실험값보다 작은 것은 벽면과의 마찰이나 유체의 온도 변화에 따른 부피 변화가 고려되지 않았기 때문으로 해당 오차는 합리적인 것으로 받아들일 수 있다. 다만 실험 중 체크밸브의 위치를 정확히 알 수 없어 임의로 고정하여 계산을 수행하였기 때문에 체크밸브의 정확한 위치가 파악될 경우 실험과 수치해석 간 결과의 차이는 감소할 것이다.

3. 결과 및 고찰

3.1 기체별 리셉터클 거리 간 압력 강하 변화

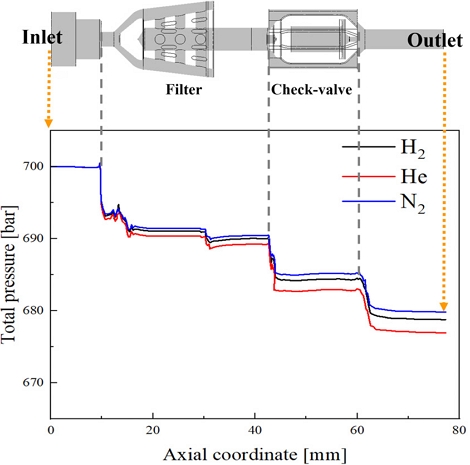
Fig. 7은 리셉터클 내부 거리에 따른 압력 변화 데이터를 나타낸 것이다. 거리에 따른 압력 변화 위치는 기체 종류와 상관없이 동일하게 나타났다. Fliter와 체크밸브 전후로 압력이 크게 변하는 구간이 3개 있는데 모든 구간에서 헬륨, 수소, 질소 순으로 압력 강하 정도가 큰 것을 알 수 있다. 수소의 실제 작동 조건인 700 bar, -40℃에서 내부 차압은 약 21 bar 발생하고 질소는 수소보다 작은 20 bar, 헬륨은 수소보다 큰 23 bar이다.

Fig. 7.

Pressure variation stream line at each receptacle position for Hydrogen and inert gas

3.2 매개변수 해석을 통한 동압-차압 상관관계 분석

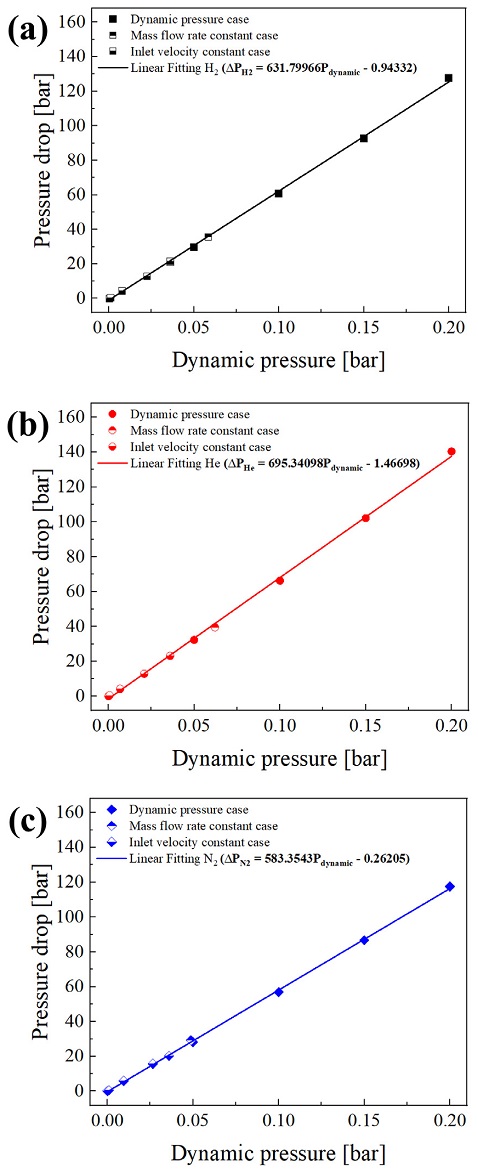
입구 조건에서 밀도, 속도, 질량 유량, 압력을 변경하며 수치해석을 수행한 결과를 Fig. 8의 동압-차압 그래프로 나타내었다. 이때 차압은 입구 압력과 출구 압력의 차로, 동압은 출구에서의 동압으로 계산하였다. 기체의 종류와 상관없이 동압에 따른 차압의 변화가 선형적인 것을 알 수 있다.

Fig. 8.

Pressure drop as a function of dynamic pressure obtained from the parameter study

각 기체의 동압-차압 선형적 관계를 수식으로 표현하였는데 수소, 헬륨, 질소 순서대로 식 (5)-(7)에 해당한다. 세 상관식은 수치해석 결과에 결정계수 0.99 이상의 높은 상관성을 가지며 기체별 고유한 기울기를 가지고 있는 것을 확인하였다.

$\[ \mathrm{\Delta }{P}_{H_2}=631.800P_{dynamic}-0.94332 \]$

(5)

$\[ \mathrm{\Delta }{P}_{He}=695.351P_{dynamic}-1.46698 \]$

(6)

$\[ \mathrm{\Delta }{P}_{N_2}=583.354P_{dynamic}-0.26205 \]$

(7)

여기서 △P는 차압, P_dynamic은 동압을 나타낸다.

3.3 불활성 기체를 이용한 수소의 차압 예측

3.2절에서 얻은 각 기체의 동압-차압 상관식의 기울기와 상수를 이용해 수소의 차압을 예측하기 위한 보정계수는 Table 2와 같다. 여기서 a는 수소의 상관식 기울기와 불활성 기체의 상관식 기울기의 비를 통해 얻었으며 b는 수소와 불활성 기체의 상관식 상수의 차로 얻을 수 있다.

Table 2.

Correction factor

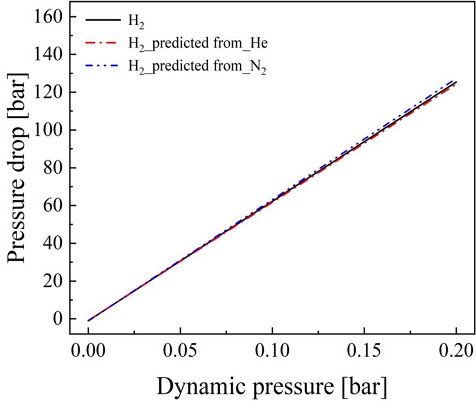
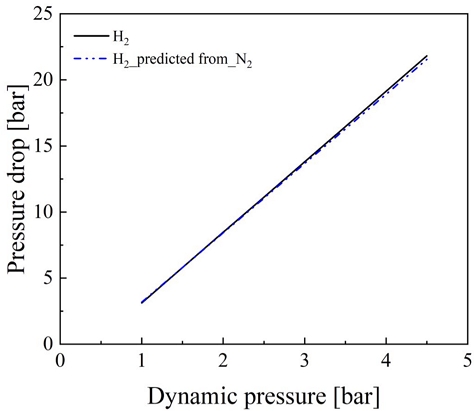
헬륨과 질소의 차압으로 수소의 차압 예측은 식 (8)과 식 (9)에 해당 보정계수를 적용하여 계산할 수 있다. 불활성 기체의 차압으로 수소의 차압을 예측한 결과를 Fig. 9에서 확인할 수 있다. 질소는 평균적으로 1.3% 크게 예측하며 헬륨의 경우 약 0.8% 작게 예측하고 있다. 오차의 크기는 동압이 커짐에 따라 커졌으며 질소는 점점 더 크게, 헬륨은 점점 더 작게 예측하였다.

$\[ \mathrm{\Delta }{P}_{H_2}=\left(\mathrm{\Delta }{P}_{He}-b\right)\mathrm{*}a \]$

(8)

$\[ \mathrm{\Delta }{P}_{H_2}=\left(\mathrm{\Delta }{P}_{N_2}-b\right)\mathrm{*}a \]$

(9)

Fig. 9.

Prediction of hydrogen pressure drop by applying the correction factor to numerical results

동일한 보정계수를 실험 결과에 그대로 적용한 결과를 Fig. 10에 나타내었다. 수치해석의 결과로만 도출한 보정계수로도 충분히 작은 수준의 오차를 나타내며 질소의 차압으로 수소의 차압을 예측할 수 있는 것을 확인하였다. 다만 실험 결과 역시 동압이 증가할수록 오차가 증가하여 동압이 매우 커진다면 수소 차압 예측의 불확도는 커질 수 있다.

Fig. 10.

Prediction of hydrogen pressure drop by applying the correction factor to experimental results

또한 수치해석 결과에 보정계수를 적용하였을 때는 과대 예측한 것에 반해 실험 결과에 적용하였을 때는 과소 예측하였다.

4. 결 론

본 연구에서는 수소와 불활성 기체 차압의 상관관계를 수치해석 기법으로 연구하였다. 기체의 종류와 무관하게 동압과 차압은 선형적인 관계를 가지며 기체별 고유한 기울기 값을 가진다. 수소와 불활성 기체 간의 관계를 이용하여 불활성 기체의 차압으로 수소의 차압을 예측할 수 있는 보정계수를 구하였다. 보정계수의 정확도는 수소와 질소의 차압 실험 결과를 이용하여 검증하였다. 검증 결과 무시할 수 있을 정도의 작은 오차를 보였기 때문에 보정계수를 이용하여 작동유체가 수소인 경우의 리셉터클 차압을 정확하게 구할 수 있을 것으로 판단된다. 다만 동압의 크기가 증가할수록 예측값의 오차가 증가하여 해석으로 얻은 결과의 불확도가 증가하였다. 향후 추가적인 실험적 연구를 통해 높은 동압 조건에서의 정확도를 향상시킬 예정이다.

Acknowledgments

본 연구는 산업통상자원부 및 산업기술평가관리원(KEIT)의 지원을 받아 수행되었습니다(과제 번호, 20015788).

References

• K. H. Oh, K. W. Lee, S. E. Lee, and T. H. Kim, “An investigation of explosion hazardous of hydrogen”, The Korean Institute of Gas Spring Annual Conference, 2006, pp. 157-162. Retrieved from https://www.dbpia.co.kr/journal/articleDetail?nodeId=NODE02072664, .
• Y. K. Kim, B. J. Park, and I. J. Hwang, “Experimental study for hydrogen explosive hazards in an open atmospheric condition”, The Korean Society of Mechanical Engineers Plant Sector 2021 Spring Annual Conference, 2021, pp. 66-67. Retrieved from https://www.dbpia.co.kr/journal/articleDetail?nodeId=NODE10564456&language=ko_KR&hasTopBanner=true, .
• J. Kwon, S. Oh, J. Choi, and Y. Kim, “A numerical analysis study of hydrogen valve to flow characteristics by fluid temperature variation for mobile charging equipment”, Journal of Hydrogen and New Energy, Vol. 33, No. 6, 2022, pp. 769-775. [https://doi.org/10.7316/KHNES.2022.33.6.769]
• S. H. Oh and H. K. Suh, “Analysis of flow performance factors according to extreme temperature conditions of hydrogen inflow of FCEV charging system check valve”, Journal of Hydrogen and New Energy, Vol. 34, No. 5, 2023, pp. 514-525. [https://doi.org/10.7316/JHNE.2023.34.5.514]
• J. U. Baek, G. M. Gwak, N. Y. Kim, Y. M. Cho, and S. K. Lyu, “Study on the optimal design of the nozzle shape of the 700 bar hydrogen refueling nozzle for hydrogen electric vehicles”, Journal of the Korean Society of Manufacturing Process Engineers, Vol. 21, No. 7, pp. 28-33. [https://doi.org/10.14775/ksmpe.2022.21.07.028]
• W. C. Park, M. S. Cheong, and C. Y. Song, “Study on structural performance by shape parameter variation of bellows for the hydrogen compressor-embedded refueling tank”, Journal of Hydrogen and New Energy, Vol. 35, No. 1, 2024, pp. 75-82. [https://doi.org/10.7316/JHNE.2024.35.1.75]
• Y. Wang, S. Lee, C. H. Sohn, S. Lee, and H. Lee, “A numerical analysis of pressure distribution and pressure drop in receptacle for hydrogen charging system”, Journal of Hydrogen and New Energy, Vol. 34, No. 5, 2023, pp. 497-504. [https://doi.org/10.7316/JHNE.2023.34.5.497]
• G. Soave, “Equilibrium constants from a modified Redlich-Kwong equation of state”, Chemical Engineering Science, Vol. 27, No. 6, 1972, pp. 1197-1203. [https://doi.org/10.1016/0009-2509(72)80096-4]
• B. J. McBride, M. J. Zehe, and S. Gordon, “NASA Glenn coefficients for calculating thermodynamic properties of individual species”, NASA, 2002. Retrieved from https://ntrs.nasa.gov/citations/20020085330, .