점성가열 효과에 의한 곡관 내 극저온 유체의 온도 변화
2024 The Korean Hydrogen and New Energy Society. All rights reserved.
Abstract
Liquid hydrogen, which operates in cryogenic environments has a density 800 times greater than gaseous hydrogen, making it advantageous for large-scale storage and transportation. However, continuous evaporation due to external heat intrusion and internal heat generation poses challenges. To mitigate heat conduction, various insulation materials are used. In pipe systems, viscous heating effects from turbulence and viscosity, especially in bends, cause heat generation. This study employs computational fluid dynamics (CFD) to analyze the impact of fluid velocity, pressure drop, inner diameter, and curvature radius of pipe bends on viscous heating. Using liquid nitrogen at 77 K as a working fluid, the CFD results showed that increased velocity and pressure drop along with smaller inner diameter and curvature radius enhanced viscous heating, raising fluid temperature.
Keywords:
Bend, Computational fluid dynamics, Cryogenic, Turbulence, Viscous heating effect키워드:
곡관, 전산 유체 해석, 극저온, 난류, 점성가열 효과1. 서 론
친환경적이고 지속 가능한 에너지원인 수소를 산업에 적용하기 위한 다양한 연구가 진행되고 있으며 특히 에너지 소실률이 높은 수소의 특성을 고려하여 저장 및 이송 장치 개발이 주목받고 있다1). 액체수소는 고압 기체수소 대비 누설 문제가 적고 저압의 환경에서 운용되기 때문에 안전성 확보에 용이하나 20 K (-253℃)의 극저온 환경에서 사용되어야 하는 제약이 따른다. 특히 저장 및 이송 시 외부로부터의 열 침입과 내부의 열 발생으로 상변화에 의한 증발가스가 발생하며 이는 에너지 밀도의 감소를 야기한다. 따라서 증발가스 발생을 억제하기 위하여 저장 및 이송용 장치의 단열 성능 향상과 관련된 연구가 활발히 이루어지고 있다.
Kwak2)은 액체수소 저장탱크용 단열 장치인 multi layer-insulation (MLI) 및 vapor-cooled shield (VCS)를 대상으로 과도 열전달 해석을 수행하였으며 얻어진 온도 및 열 유속 결과로부터 단열 효율 향상을 위한 MLI 및 VCS 시스템을 제안하였다. Oh 등3)은 액체수소용 진공단열 자켓 밸브에 대하여 진공도 10-1-10-4 Torr에서 진공단열 성능을 분석하였다. 진공도 증가에 따라 단열 성능이 향상되었으며 열 침입을 막기 위하여 최소 10-3 Torr 이상의 진공도를 유지해야 함을 제시하였다. Seo 등4)은 액체수소 진공단열 저장탱크의 열전도와 증발가스 발생률의 상관관계를 수치 해석을 통해 분석하였다. 저장탱크의 용량과 내압에 따라 초기에는 증발가스가 발생하지 않으며 일정 시간 후 내압이 설계 압력에 도달할 때까지 증발가스 양은 증가하였다. 그러나 운영 시간에 따른 증발가스 발생량에는 큰 차이가 나타나지 않음을 확인하였다.
상기 연구 사례는 액체수소 저장 및 이송 장치의 진공도와 열전도에 따른 단열 효과 대한 연구로 외부로부터의 열 침입은 평가되었으나 내부의 열 발생은 충분히 고려하지 못하였다. 액체수소의 기화점은 극저온인 약 22 K이며 이를 유지하기 위한 극저온 냉각 기술 및 단열 기술에 대한 비용은 높게 형성되어있다. 따라서 액체수소의 온도 상승은 증발가스 발생으로 인한 에너지 손실로 이어지며 이는 비용적, 에너지 효율적으로 큰 손실로 나타나게 된다. 따라서 극저온 유체가 이송되는 배관에서 외부 열 침입뿐만 아니라 내부 열 발생 또한 반드시 고려되어야 한다.
배관의 경우 액체수소의 내부 유동에 의하여 벽면 근처의 전단력과 난류로 인하여 점성가열 효과(viscous heating effect)가 나타나며5) 이는 배관 내부의 열 발생을 유발하여 증발가스 발생의 주요한 원인이 될 수 있다. 특히 작동유체에 의한 내부 열 발생은 속도와 압력 변화에 의해 전단력이 크게 발생하는 곡관에서 두드러지게 나타나므로 곡관 설계 시 내부 열 발생을 면밀히 검토하여야 한다.
본 연구에서는 액체수소 저장탱크 시스템에 적용되는 곡관을 대상으로 증발가스 발생의 원인 중 하나인 내부 열 발생을 평가하기 위하여 곡관의 형상 설계변수를 고려한 전산 유체 해석을 수행하였다. 본 연구는 재료 특성의 관점이 아닌 열역학 및 유체역학적 관점으로 진행되었기 때문에 전산 유체 해석 시 비교적 선행 연구 및 물성 자료가 풍부하며 초저온 환경에서 운영되는 액체질소를 작동유체로 대체하였다. 그리고 곡관의 곡률반경6) 및 내경에 따른 곡관 내 유동장의 속도 및 난류 운동에너지 변화를 고려하여 내부 열 발생에 의한 유동장의 온도 변화를 해석적으로 구하였다.
2. 수치 해석 모델
점성가열 효과는 유체의 점성으로 배관 벽과 유체 사이에서 발생하는 전단력에 의한 마찰로 열이 발생하는 현상이다. 발생된 열은 유체의 열적 물성 값을 변화시키며 특히 초저온 작동유체는 끓는점에 인접한 온도 범위에서 운용되기 때문에 점성가열 효과로 인한 낮은 발열에도 기화하기 쉽다. 따라서 효율적인 이송을 위하여 배관 내에서 발생하는 점성가열 효과를 고려하여야 한다.
이차원 유동장에서 평판의 길이를 L, 평판 간의 거리를 2H, H/L을 1로 하였을 때 유체가 비압축성 균질 유체이고 속도가 U라면 에너지 방정식7)은 다음과 같다.
| (1) |
여기서 ρ는 유체의 밀도, v는 속도벡터, h는 엔탈피, T는 온도, k는 열전도율 그리고 τ는 응력 텐서이며 유체 내부의 전단력을 의미한다.
응력 텐서 τ를 포함한 항은 점성가열 효과에 의해 열을 발생시키는 주요 성분이다. 엔탈피 h는 온도와 일정한 비열의 곱으로 주어지고 부력이 유동에 미치는 영향은 없다고 가정하면 응력 텐서와 변형률 사이의 관계는 다음과 같이 무차원 항으로 나타낼 수 있다.
| (2) |
여기서 는 무차원 시간이며 (ζi,ζj)는 (x/H, z/H)로 x와 z를 특정 길이 H로 나눈 값이다. ζi 및 ζj는 종방향 및 횡방향의 무차원 좌표를 의미한다. (ui,uj)는 (ux/U*,uy/U*)로 특성 속도 U*로 정규화된 무차원 유체 속도이고 θ는 -β(T-T0)로 무차원 온도이다. β 및 T0는 온도 특성 변화율 및 참조 온도를 의미한다.
Pe는 페클레 수(Peclét number)이며 연속체의 이동 현상과 관련된 무차원 수로 다음과 같이 나타낼 수 있다.
| (3) |
여기서 Cp는 비열 용량으로 대류 및 전도에 의한 열 전달량의 비율을 의미한다.
한편 Br은 브랑크만 수(Brinkman number)이며 전도에 의한 열에너지가 운동에너지로 소산되는 비율로 다음과 같다.
| (4) |
여기서 ∇T는 기준 온도 T0를 기준으로 온도 변화이며 μ는 평균 점성이고 식 (5)와 같이 나타낼 수 있다.
| (5) |
여기서 μ0는 기준 온도 T0에서의 점성을 의미한다.
Br 값을 유체 물성치 및 유동 관련 값으로 분리하면 다음과 같다.
| (6) |
식 (6)을 이용하여 Br은 다음과 같이 두 개의 특성 값으로 나타낼 수 있다.
| (7) |
여기서 Pr은 유체의 점성과 열에너지 확산력에 관련된 무차원 수인 프란틀 수(Prandtl number)이며 유체의 물성치에 의해 구할 수 있다. Ec는 점성 소산에 관련된 무차원 수인 에커트 수(Eckert number)이며 표면의 열에너지 차와 운동에너지의 비율에 관한 값을 나타낸다.
무차원으로 표현된 응력 텐서 τ와 열전달 항에 포함된 브랑크만 수 Br를 이용하면 유체의 점성으로 인한 마찰력으로 발생되는 열을 추정할 수 있다.
브랑크만 수 Br에 의하여 유체의 속도가 유동에 지배적인 경우 구할 수 있는 점성가열 효과와 함께 난류에 의해 생성되는 효과 또한 고려하여야 한다. 이를 위하여 다음과 같은 난류 운동에너지 방정식이 이용된다.
| (8) |
k는 난류 운동에너지, Uj는 평균 속도 성분, -u'iu'j는 레이놀즈 응력, v는 동점성계수 그리고 ϵ는 난류에너지 소산율을 의미한다. 이때 난류에너지 소산율 ϵ은 아래와 같다.
| (9) |
ϵ은 난류에너지가 점성 소산을 통해 열에너지로 변환되는 비율을 나타내며 식 (9)는 난류 운동에너지가 점성력에 의해 소산되는 과정과 난류 유동으로 발생하는 에너지가 어떻게 열로 변환되는지를 설명한다.
3. 전산 유체 해석
초저온 유체 저장탱크 시스템에 적용되는 곡관의 경우 곡률이 적용되는 엘보우에서 작동 유체의 압력 및 속도 구배에 의하여 유체 내부에 전단력이 나타나며 이는 유체의 점성 마찰력을 유발하여 열이 발생한다. 따라서 곡관 엘보우의 곡률반경 변화에 따른 유체 전단력과 점성가열에 의한 온도 변화를 전산 유체 해석으로 평가하였다.
유체 전단력은 난류 운동에너지와 비례한다. 따라서 식 (1)과 같은 에너지 방정식을 전산 유체 해석으로 계산된 난류 운동에너지(turbulence kinetic energy)로 치환하여 평가하였다8). 유체 입자 간 전단력은 유동 시 속도 섭동(velocity fluctuation)으로 속도가 다른 입자들이 빈 공간을 채우며 나타나는 서로 다른 방향의 유동에 의한 유체의 점성으로 인하여 발생한다9). 점성에 의한 전단력은 특히 곡관 엘보우의 벽면 부근에서의 유동 흐름의 변형을 야기하고 이로 인해 유동은 와도(vorticity) 및 와류(eddy)와 같은 난류로 발달하게 된다.
한편 점성가열은 식 (7)과 같이 유체 전단력의 항인 응력 텐서 τ에 포함된 브랑크만 수 Br을 구성하는 프란틀 수 Pr과 에커트 수 Ec로부터 구할 수 있다. 여기서 Pr은 작동 유체의 물성치로 본 연구에서는 액체질소의 Pr인 2.25를 적용하였다. 한편 유체의 속도와 Ec는 비례 관계를 보이며 속도의 감소에 따라 Br은 감소하게 되고 이는 운동에너지가 열에너지로 발산되는 것을 유발하여 점성가열 효과가 나타난다.
3.1 해석 전처리
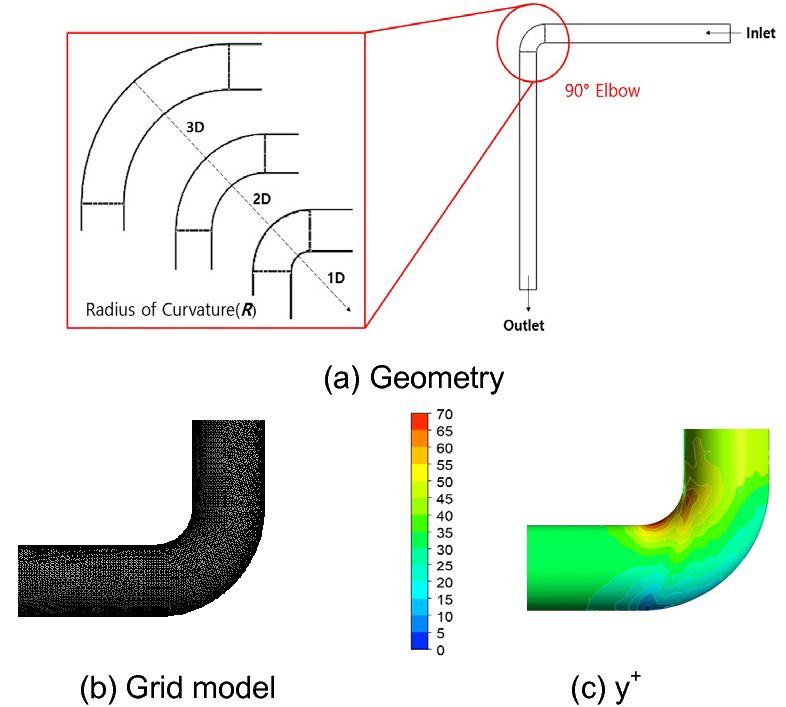
내경이 D인 90° 곡관 엘보우의 곡률반경 R에 따른 난류 운동에너지와 점성가열에 의한 온도 변화를 평가하기 위하여 R을 내경의 비로 표현한 세 가지 모델(1D, 2D, 3D)이 Fig. 1(a)와 같이 설정되었다. 여기서 진공단열 배관을 생산하는 기업의 제품 사양을 고려하여 내경 D는 90 mm로 하였으며 완전히 발달된 유동의 관찰을 위해 입, 출구단 길이는 각각 10D 및 12D로 하였다. 전산 유체 해석은 상용 해석 프로그램인 ANSYS Fluent 17.2 (Ansys, Canonsburg, PA, USA)로 수행되었으며 해석을 위해 사용된 컴퓨터의 사양은 IntelⓇ XeonⓇ CPU E5-2630 v4 @ 2.20 GHz (Intel, Santa Clara, CA, USA)이다. 효율적인 계산을 위하여 Fig. 1(b)와 같은 면대칭 경계 조건을 적용한 3차원 격자 모델이 사용되었다.
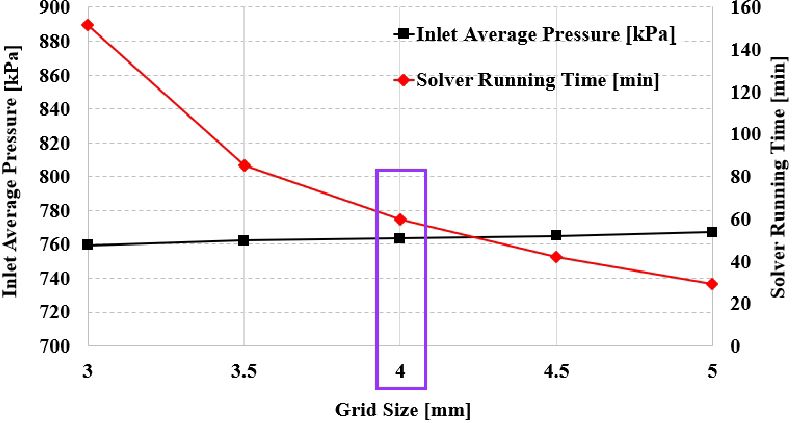
격자 선정에 앞서 과도한 해석 시간을 줄이는 동시에 격자의 신뢰성 검증을 위해 격자 수렴성 검사(gird convergence test)를 수행하였다. 격자 수렴성 검사를 위한 다양한 격자 크기별 정보를 Table 1에 정리하였으며 이에 따른 검사의 결과를 Fig. 2에 도시하였다. 수렴성 검사를 통해 #3 수준의 격자를 최종적으로 선정하였으며 해당 격자의 y+는 Fig. 1(c)와 같이 69.8이다. 적용된 난류 모델은 Reynolds averaged Navier Stokes (RANS)식 중 벽면에서의 열전달 및 전단력 구현 정도가 높은 k-ω shear stress transport (SST)이다10,11). 작동 유체는 액체질소이며 입구에서 유량이 0.36 m3/s인 77 K (-196℃)의 경계 조건이 사용되었다. 해당 경계 조건은 Lee12)에 의해 연구된 액체질소 파이프 내부 열 유동 분석에서 사용한 경계 조건을 참고하여 차압이 7 bar일 때의 유량이다. 또한 내부의 열 발생 및 전달 현상을 집중적으로 분석하기 위해 벽에는 단열 조건을 사용하였다. 액체질소의 물성치와 전산 유체 해석의 하중, 경계 조건은 Table 2, Table 3과 같다.
3.2 해석 결과
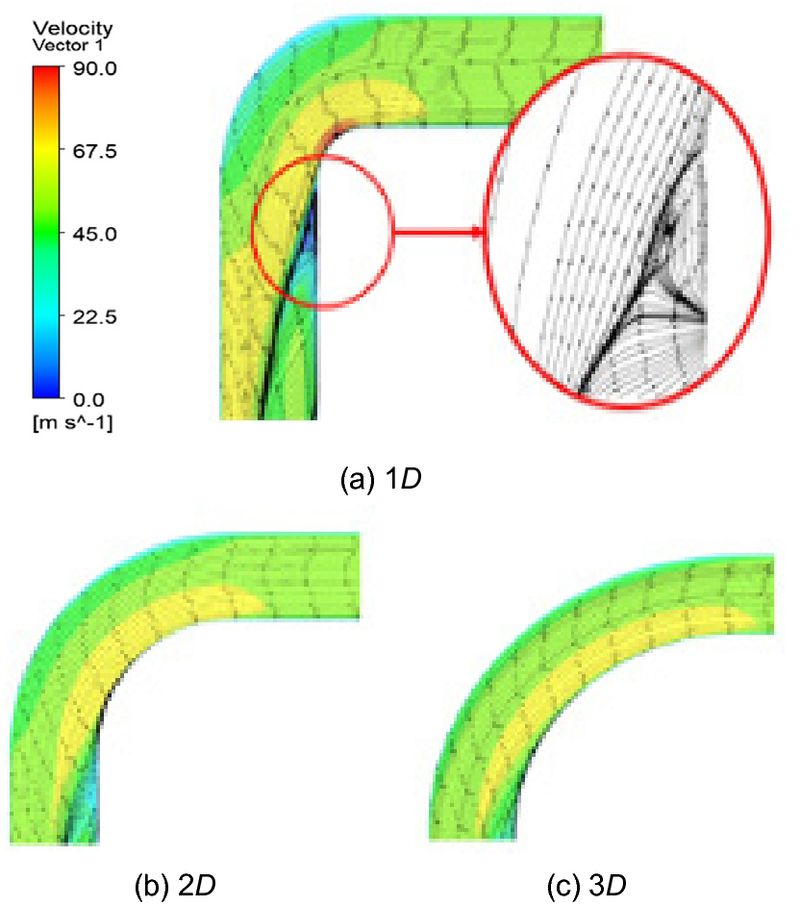
Fig. 3은 전산 유체 해석으로 얻어진 90° 곡관 엘보우의 곡률반경 R에 따른 속도 벡터의 분포이다. R=1D인 경우 Fig. 3(a)와 같이 곡률의 중심 벽면에서 90 m/s의 최고 속도가 나타나며 이후 난류에 의해 2차 유동장 영역으로 구분되는 뚜렷한 유동 박리가 나타났다. 이는 Kato 등13)에 의해 연구된 곡관에서의 난류 유동 특성의 입자 이미지 유속계(particle image velocimetry) 결과와 유사한 경향성을 보이고 있다. 따라서 본 연구에서 제안된 CFD 모델이 곡관에서의 유동이 잘 모사되고 있음을 확인하였다. 다음으로 R=2D의 결과인 Fig. 3(b)를 보면 유체의 최고 속도가 67.5 m/s로 감소하며 이후 일부 난류 유동이 나타나지만 R=1D와 같은 뚜렷한 유동박리가 나타나지 않아 2차 유동장은 발생하지 않았다. R=3D에서는 Fig. 3(c)와 같이 최고 속도는 R=2D와 유사하며 난류 유동은 나타나지 않았다.
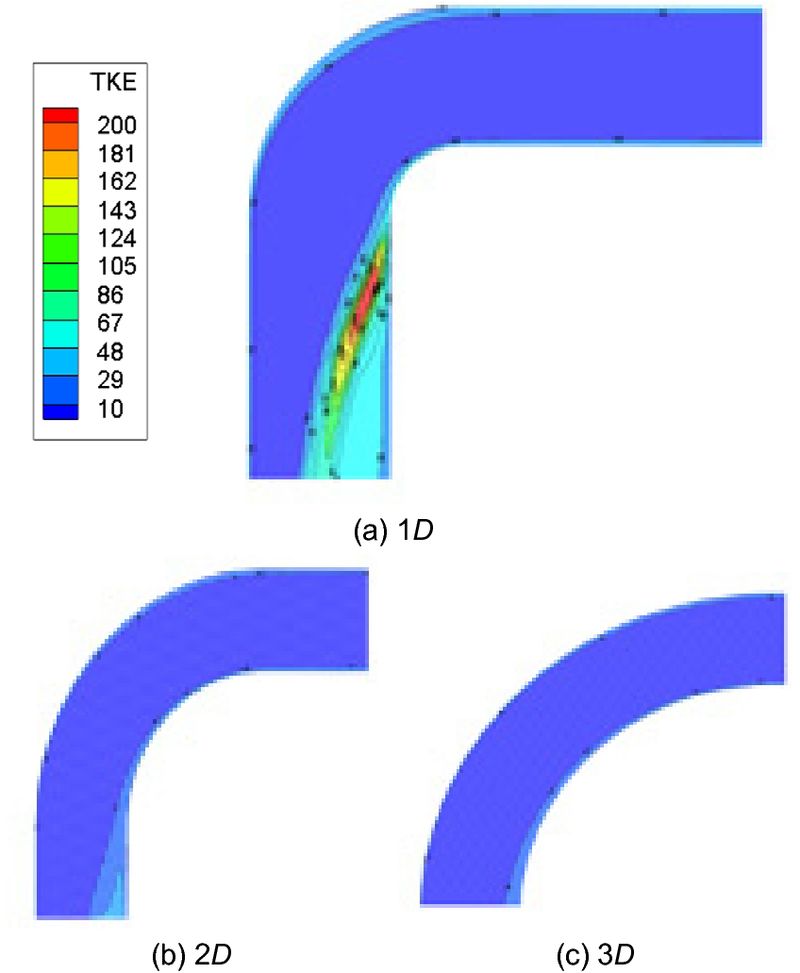
Fig. 4는 난류 운동에너지(m2/s2)의 분포를 나타낸 것이며 R=1D인 경우 Fig. 4(a)와 같이 곡률이 끝나는 부분의 벽면에서 난류 운동에너지는 최대 200 m2/s2로 나타난다. 전단력에 의한 뚜렷한 난류 유동장이 생성되고 출구단까지 48 m2/s2 이상의 넓은 범위에서 난류 유동이 발달되었다. R이 커지는 경우 난류 운동에너지가 급격히 감소하였으며 R=2D인 경우 Fig. 4(b)와 같이 난류 운동에너지가 소폭 증가하였지만 난류 유동이 미미한 것으로 판단되고 R=3D에서는 Fig. 4(c)와 같이 난류 유동장이 나타나지 않았다.
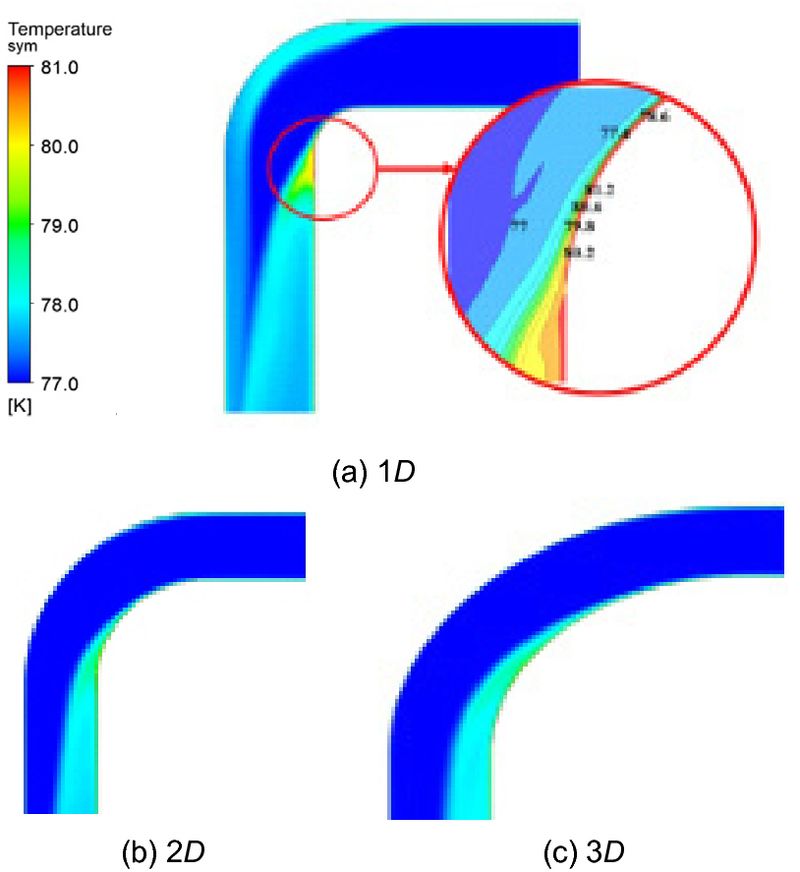
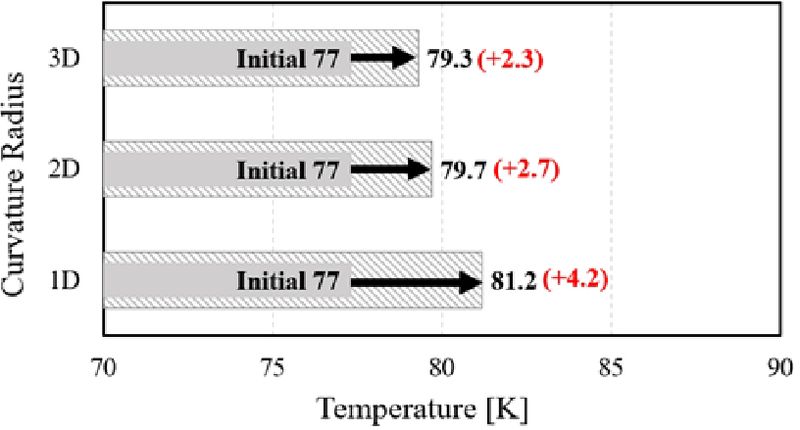
한편 90° 곡관 엘보우 내 유동장의 온도 분포는 Fig. 5와 같으며 곡률반경에 따른 온도의 증가는 Fig. 6에 그래프로 도시화하였다. R=1D인 경우 Fig. 5(a)와 같이 유동박리에 의해 나타나는 2차 유동장의 시작 위치 및 곡관 내부 벽면에서 유체 온도가 최고 4.2 K 증가한 81.2 K로 나타났다. 유동 단면적 변화에 의하여 곡률을 가진 부분에서 속도 증가 현상이 나타나게 되며 점성에 의한 전단력의 영향으로 난류 운동에너지가 증가하였다11). 따라서 점성, 속도와 비례하는 점성가열 효과로 인하여 벽과 가까운 부분에서 가장 높은 온도가 나타나는 것을 볼 수 있다7).
R=2D인 경우 Fig. 5(b)와 같이 일부 난류 유동으로 인해 최고 속도가 나타난 지점에서 유체의 온도는 2.7 K 증가한 79.7 K로 나타났으며 Fig. 5(c)의 R=3D에서의 최고 온도는 2.3 K 증가한 79.3 K으로 R=2D와 유사한 온도 분포를 보이고 있다. 곡률반경이 큰 경우 크게 난류가 발생하지 않는 비교적 안정적인 유동을 보였으며 온도 증가가 거의 없음을 해석적으로 확인하였다.
난류에너지가 열에너지로 소산되는 비율을 나타내는 난류에너지 소산율 ϵ을 도출하기 위하여 식 (9)를 이용하여 최고 온도 81.2 K 및 최저 온도 77 K 지점에서 계산한 결과 각각 1.92 및 1.51로 도출되었다. 따라서 난류 운동에너지가 증가하여 난류 소산에 의해 벽과 떨어진 부분에서 열 발생이 일어났음을 확인할 수 있었다. 또한 점성가열 효과에 의해 발생하는 온도 상승 효과보다 미미한 것을 확인하였다. Perez 등14)이 연구한 바에 따르면 액체질소 저장탱크에서 약 4시간 동안 1.7 K의 온도가 상승할 경우 1.2 K 상승한 탱크보다 증발가스 발생량이 15% 더 증가하였다. 본 연구에서는 유체 이송 시를 가정하고 있으므로 지속적으로 고온에 노출되는 저장탱크의 연구 결과보다는 낮은 증발가스 발생 증가량이 예상된다. 하지만 온도 상승값이 높게 나타나 흐르는 유체 상태더라도 증발가스 발생에 충분히 영향을 미칠 것으로 판단된다. 따라서 점성가열 효과로 인하여 상승한 내부 온도는 액체질소에서 증발가스 발생을 유발하는 충분한 온도 상승으로 확인된다.
4. 고 찰
앞서 수행한 해석을 통한 곡률반경에 따른 점성가열 효과에 대한 평가로부터 R=1D의 곡률반경에서 점성가열 효과가 가장 큰 것으로 확인되었다. 또한 Fig. 3(a)의 해석 결과에서 엘보우 내부에서 급격한 속도 변화에 의한 난류로 2차 유동장 영역이 나타나며 이는 엘보우 내부의 압력 변화에도 큰 영향을 미칠 것으로 판단된다. 따라서 R=1D의 곡률반경 조건에서 초기 엘보우의 지름 D=90 mm에서 30 mm씩 증감한 60 mm 및 120 mm의 세 가지 모델에 대하여 엘보우 내부의 압력 변화를 관성력에 대한 압력의 상대적인 비를 나타내는 압력계수(pressure coefficient, Cp)를 이용하여 평가하였다.
| (10) |
여기서 P는 지점별 압력(MPa), P0는 출구 압력(대기압, 101.325 MPa), ρ는 유체 밀도(액체질소, 0.805 kg/m3) 그리고 Vin,mean는 엘보우 입구에서의 유체 평균 속도(m/s)이다. 평균 속도는 D=60, 90, 120 mm에 대하여 각각 81, 72, 65 m/s이다.
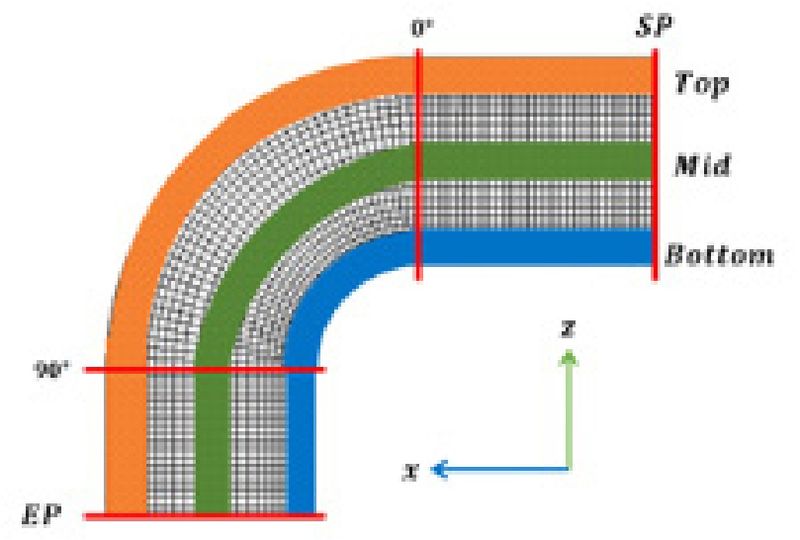
엘보우 내부 유동층에 따른 Cp 변화를 살펴보기 위하여 Fig. 7과 같이 유동층을 top-, mid- 및 bottom-층으로 나누었으며 유동 방향에 따른 각 유동층의 구간을 곡관 시작점에서 엘보우 입구까지를 start point (SP)-0°, 엘보우 입구에서 출구까지를 0°-90° 그리고 엘보우 출구에 곡관 종단점을 90°-end point (EP)로 표기하였다.
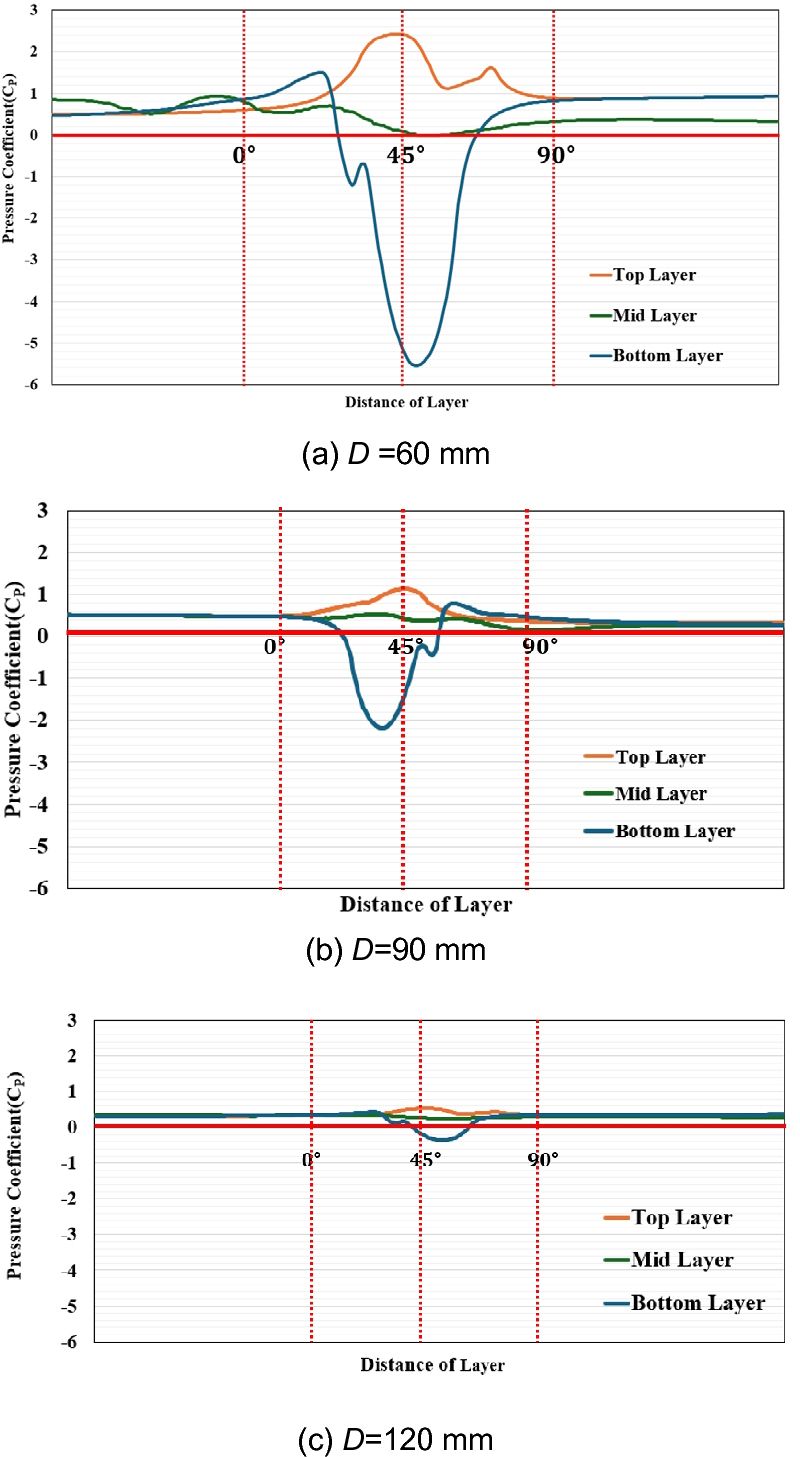
Fig. 8은 해석 결과로 Cp는 top- 및 mid-층에서 큰 변화를 보이지 않으나 bottom-층 엘보우 입구 및 출구 ρ구간 0°-90°에서 급격한 변화를 보이며 큰 폭으로 감소하였다. Bottom-층에서의 Cp 감소폭은 엘보우의 지름 D가 가장 작은 60 mm에서 제일 크게 나타났다. 이를 통해 bottom-층 엘보우 중심부(45°)에서 Cp는 -5.55로 대기압 이하의 상태임을 알 수 있다. D가 90 mm 및 120 mm인 경우 bottom-층 엘보우 중심부(45°)에서 Cp는 -2.32 및 -0.38로 D=60 mm에 비하여 증가하지만 대기압보다는 낮은 상태이므로 작동유체인 액체질소의 공동 현상 발생이 가능할 것으로 사료된다. 따라서 엘보우가 설치된 초저온용 곡관의 설계 시 점성가열 효과뿐만 아니라 공동 현상 방지를 고려해야 할 것으로 판단된다.
5. 결 론
본 연구에서는 극저온 액체 수송 시스템 곡관에 사용되는 엘보우의 곡률반경 R, 내경 D 그리고 유량Q가 점성가열 효과에 미치는 영향을 검토하기 위해 ANSYS Fluent 17.2v를 활용한 CFD 해석을 수행하였다. 본 연구를 통해 다음과 같은 결론을 얻었다.
1) D=90 mm 및 Q=0.36 m3/s인 조건에서 R이 작은 경우 엘보우 내 벽 안쪽에서 불안정한 유동 및 유동 박리가 발생한 반면 R이 큰 경우 상대적으로 안정적인 유동이 나타났다. 이때 R=1D에서 액체질소의 온도는 77 K에서 81.3 K로 상승하여 점성가열 효과가 나타남을 확인하였다.
2) 사례 연구를 통해 D와 R이 감소할수록 그리고 Q가 증가할수록 점성가열 효과가 뚜렷하게 나타나 직경 60 mm, R=1D 그리고 Q=0.36 m3/s 인 조건에서 액체질소의 온도는 90.3 K로 초기온도 대비 13.3 K 이상 상승함을 확인하였다.
3) D에 따른 내부 압력 변화를 관찰하기 위해 압력계수(Cp)를 활용하였다. Cp는 모든 사례 연구에서 top-, mid-층은 큰 변화를 보이지 않았다. D가 가장 작은 60 mm의 경우 엘보우의 중심부(45°)에서 가장 큰 Cp의 감소폭을 보여 -5.55로 나타났으며 D가 90, 120 mm인 경우 같은 위치에서 -2.32, -0.38로 나타났다. 이는 D=60 mm인 경우 큰 압력 감소를 보이며 공동 현상이 발생할 수 있을 것으로 판단하였다.
4) 본 연구 결과를 통해 극저온 액체의 운송 시스템 곡관에 사용되는 엘보우의 내경 D, 유량 Q 그리고 적절한 곡률반경 R을 선정하여 점성가열 효과로 인한 증발 현상을 최소화할 수 있을 것으로 기대된다.
Acknowledgments
본 논문은 부산광역시 및 (재)부산테크노파크 BB21plus 사업의 지원을 받았음.
References
-
C. Kim, G. Kim, and H. Kim, “Analysis of domestic and foreign policy and technology trends for hydrogen industry development”, Journal of Hydrogen and New Energy, Vol. 34, No. 2, 2023, pp. 122-131.
[https://doi.org/10.7316/JHNE.2023.34.2.122]

-
H. S. Kwak, “Design of insulation for liquid hydrogen storage tank using heat transfer analysis”, Transactions of the Korean Society of Mechanical Engineers - A, Vol. 47, No. 12, 2023, pp. 937-944.
[https://doi.org/10.3795/KSME-A.2023.47.12.937]

-
S. J. Oh, K. S. Jeon, J. H. Yoon, and J. Choi, “A study on the thermal characteristics of the vacuum jacket valve for transporting liquefied hydrogen according to the degree of vacuum”, Journal of Hydrogen and New Energy, Vol. 32, No. 6, 2021, pp. 585-591.
[https://doi.org/10.7316/KHNES.2021.32.6.585]

-
H. S. Seo, Y. Lee, D. Kim, and C. Park, “Insulation performance and BOR of pressurized large-capacity liquid hydrogen storage tank”, Journal of Hydrogen and New Energy, Vol. 34, No. 6, 2023, pp. 650-656.
[https://doi.org/10.7316/JHNE.2023.34.6.650]

- Y. H. Jeong, J. O. Lee, and T. J. Park, “CFD analysis of proportional control valve with viscous heating”, Proceedings of KSPE 2013 Spring Conference, 2013, pp. 957-958. Retrieved from https://www.dbpia.co.kr/Journal/articleDetail?nodeId=NODE02207143, .
- S. J. Kim, S. H. Hyun, J. G. Hong, and I. H. Min , “The effect of the curvature of pipe on the thermal-flow field”, Journal of Industrial Technology, Vol. 19, 1999, pp. 1-8. Retrieved from https://scholar.kyobobook.co.kr/article/detail/4010026270622, .
- A. Costa and G. Macedonio, “Viscous heating effects in fluids with temperature-dependent viscosity: triggering of sec-ondary flows”, Journal of Fluid Mechanics, Vol. 540, 2005, pp. 21-38. Retrieved from https://www.cambridge.org/core/journals/journal-of-fluid-mechanics/article/abs/viscous-heating-effects-in-fluids-with-temperaturedependent-viscosity-triggering-of-secondary-flows/429202914648086E59D79296A7DF8849#, .
-
N. D. Pope, J. Widdows, and M. D. Brinsley, “Estimation of bed shear stress using the turbulent kinetic energy approacha comparison of annular flume and field data”, Continental Shelf Research, Vol. 26, No. 8, 2006, pp. 959-970.
[https://doi.org/10.1016/j.csr.2006.02.010]

-
A. Paglietti, “The laminar-to-turbulent transition in viscous fluid flow”, Continuum Mechanics and Thermodynamics, Vol. 29, No. 2, 2017, pp. 611-623.
[https://doi.org/10.48550/arXiv.1703.07223]

- W. Wróblewski and D. Frączek, “Heat transfer modelling in a rotating cavity using the SST k-ω turbulence model”, Archives of Mechanics, Vol. 66, No. 5, 2014, pp. 343-364. Retrieved from https://am.ippt.pan.pl/am/article/view/v66p343, .
-
F. Rütten, W. Schröder, and M. Meinke, “Large-eddy simulation of low frequency oscillations of the Dean vortices in turbulent pipe bend flows”, Physics of Fluids, Vol. 17, No. 3, 2005, pp. 035107.
[https://doi.org/10.1063/1.1852573]

- J. H. Lee, “A study on the heat transfer characteristics according to the degree of vacuum for a double insulating pipe [Doctoral dissertation]”, Busan: Dong-A University, 2017.
-
Y. Kato, K. Fujimoto, G. Guo, M. Kawaguchi, M. Kamigaki, M. Koutoku, H. Hongou, H. Yanagida, and Y. Ogata, “Heat transfer characteristics of turbulent flow in double-90°-bend pipes”, Energies, Vol. 16, No. 21, 2023, pp. 7314.
[https://doi.org/10.3390/en16217314]

-
F. Perez, S. Z. S. Al Ghafri, L. Gallagher, A. Siahvashi, Y. Ryu, S. Kim, S. G. Kim, M. L. Johns, and E. F. May, “Measurements of boil-off gas and stratification in cryogenic liquid nitrogen with implications for the storage and transport of liquefied natural gas”, Energy, Vol. 222, 2021, pp. 119853.
[https://doi.org/10.1016/j.energy.2021.119853]