Linde-Hampson 및 Claude 사이클을 이용한 산소액화공정 연구
2022 The Korean Hydrogen and New Energy Society. All rights reserved.
Abstract
In this paper, comparative studies between Linde-Hampson and Claude cycle for the liquefaction of oxygen have been completed. PRO/II with PROVISION release 2021. 1 from AVEVA company (Cambridge, UK) was used, and Peng-Robinson equation of the state model with Twu’s alpha function was selected for the modeling of the condensation of oxygen. When using Claude liquefaction cycle, we could reduce the total compression power by 59.51% for the comparison of Linde-Hampson cycle.
Keywords:
Linde-Hampson cycle, Claude cycle, Oxygen liquefaction, Computer simulation, Equation of state키워드:
린데 햄프슨 사이클, 클라우드 사이클, 산소 액화, 전산 모사, 상태방정식1. 서 론
산소와 질소 혹은 주 성분이 산소와 질소의 혼합물인 건조 공기 등과 같이 상온에서는 초임계 상태로 존재하는 끓는점이 매우 낮은 기체를 액화시키는 방법 중에 가장 대표적인 방법으로 Joule-Thomson 팽창 효과를 이용하는 것을 예로 들 수 있다1-3). 고압의 기체를 줄-톰슨 팽창 밸브를 통해서 급격하게 압력을 떨어뜨리면 등엔탈피 과정이기 때문에 압력 강하 효과로 인해서 액체의 증발이 일어나면서 잠열에 의해서 온도가 급격하게 떨어지게 되는 원리를 이용하는 것이다.
수소와 헬륨을 제외하고 대부분의 유체는 포화 또는 과냉각 액체 상태에서 급격히 압력을 떨어뜨리면 증발이 일어나면서 팽창 밸브 후단에서 낮은 온도를 얻을 수 있다. 팽창 밸브 후단에서 증발되지 않은 나머지 저온의 액상의 유체를 공정 유체와 열교환 시킴으로써 냉동 효과를 얻을 수 있다.
Table 1에는 4가지 기체에 대해서 입구 압력 100 bar에서 도출압력을 Joule-Thomson 팽창 효과를 이용하여 1 bar까지 급격하게 낮추었을 때 출구 온도와 온도 차이를 나타낸 것이다4). Table 1에 의하면 메탄과 질소의 경우에는 모든 경우에 있어서 팽창 밸브 후단에서 온도가 떨어지는 것을 알 수 있다. 하지만 헬륨과 수소의 경우에는 오히려 온도가 상승하는 것을 알 수 있다.
기체 성분의 액화를 위한 또 다른 방법으로는 팽창기를 이용하는 것이다. 팽창기는 기체 압축기와 반대 과정이기 때문에 기체 압축기를 사용하면 외부에서 동력이 소모되는 것이고, 팽창기를 사용하는 것은 고압의 기상의 유체의 압력을 급격히 떨어뜨리면서 동력을 얻게 되는 것이다.
본 연구에서는 상온 및 상압 조건에 있는 산소를 액화하기 위해서 Linde-Hampson 및 Claude의 기체 액화 사이클을 이용해서 각각 액화 산소를 얻는 공정에 대한 전산모사를 통한 비교 연구를 수행하였다.
2. 열역학 이론
본 연구에서 사용한 산소 액화를 위한 두 가지 냉동 공정의 전산 모사에 사용한 열역학 모델식은 Peng-Robinson (PR) 상태방정식이다5,6). 비삼차형 상태방정식으로는 Benedict-Web-Rubins-Starling (BWRS) 및 GERG-2008 모델식 등이 있다7-9). 한편 차세대 상태방정식 모델식으로 구분되는 SAFT 모델식과 PC-SAFT 모델식의 경우에는 정확성은 뛰어난 모델식이지만 순수성분 매개변수조차 화학공정 모사기에 내장되어 있지 않기 때문에 현재에는 그 사용이 매우 제한적이라는 단점이 있다.
본 연구에서 사용한 PR 상태방정식의 functional form은 식 (1)과 같이 나타낼 수 있다. PR 상태방정식은 주로 천연가스의 K-value를 추산하는 데 사용되기는 하지만 증기상과 액상의 엔탈피, 엔트로피 추산에도 적용된다. 그리고 증기상의 밀도 추산에도 사용되는 모델식이다. 그러나 액상의 밀도 추산에는 가능은 하지만 그 정확성이 다소 떨어지는 단점이 있기 때문에 액상의 밀도 추산에는 API 상관 관계식을 자동적으로 채택하도록 하고 있다.
| (1) |
식 (1)에서 a와 b는 각각 에너지 매개변수와 크기 매개변수이다. 이는 임계온도와 임계압력의 함수로 식 (2) 및 식 (3)과 같이 유도된다.
| (2) |
| (3) |
또한 α는 알파 함수로써 Pitzer가 제안한 편심인자를 사용한 것을 개선하기 위해서 Twu 등10)이 제안한 식 (4)와 같은 식을 사용하였다.
| (4) |
Table 2에는 산소에 대한 식 (4)의 Twu 등10)이 제안한 새로운 alpha function의 계수들을 나타내었다. 이는 최초의 PR 상태방정식에서는 산소의 이심인자를 이용하여 산소의 온도에 따른 증기압을 추산하는 반면에 산소의 온도에 따른 실험 데이터의 회귀분석을 통해서 각각의 매개변수들을 결정한 것이므로 증기압 실험 데이터를 좀 더 잘 추산한다고 할 수 있다.
3. 전산모사
산소의 액화를 위한 Linde-Hampton 사이클과 Claude 사이클을 이용한 공정의 전산 모사를 위해서 AVEVA 사(Cambridge, UK)의 PRO/II with PROVISION Ver. 2001.1을 사용하였다. 범용성 화학공정 모사기로는 Aspen Plus와 Aspen HYSYS 등이 더 있으나 열역학 모델식으로 Peng-Robinson 상태방정식을 사용하기 때문에 전산모사기 종류에 따른 모델링 결과의 차이는 거의 없을 것으로 사료된다.
액화를 위한 산소의 조건은 Table 3에 나타내었다. 공급 온도는 11.5℃이며, 압력은 대기압보다 약간 높은 0.0622 kg/cm2G이며, 부피 유량은 10,000 Nm3/h를 기준으로 산소 액화공정에 대한 전산모사를 수행하였다.
위에서 언급한 것처럼 산소 액화공정의 전산 모사를 위한 열역학 모델식으로는 Peng-Robinson 상태방정식을 적용하였으며, AVEVA 사의 PRO/II with PROVISION Ver. 2021.1 (PRO/II)을 사용하였다.
3.1 Linde-Hampson 사이클에 의한 산소액화공정의 전산 모사
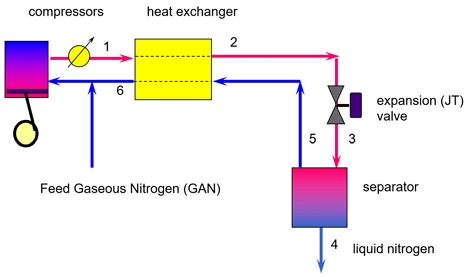
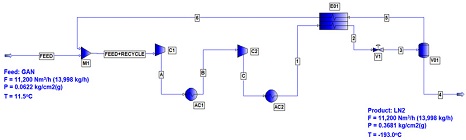
Fig. 1에는 Linde-Hampson의 산소액화공정에 대한 개요도를 나타내었다. Fig. 1에 의하면 원료 기체가 6번 스트림으로 환류되는 기체와 합쳐진 다음에 압축기로 주입되어 가압된 후 열교환기에 의해서 예냉된다. 그리고 Joule-Tomson 팽창 밸브에 의해서 급격하게 대기압 근처까지 압력이 낮아진 후 부분 응축이 일어난다. 이때 액화되지 않은 저온의 산소기체는 원료 기체와 열교환된다. Fig. 2에는 Linde-Hampson 사이클에 대한 PRO/II를 이용한 산소액화공정에 대한 flow sheet를 나타내었다. Fig. 2에 의하면 원료로 주입되는 산소 14,627 kg/h는 전량 -179.8℃ 조건에서 액화가 일어난다. 액화되지 않고 환류되는 산소기체는 약 404,732 kg/h로써 원료 질소 기체의 약 28.35배가량에 이른다.
Fig. 2에 의하면 Linde-Hampson 사이클에 의한 산소액화공정은 중간에 냉각기를 가지는 2기의 압축기를 사용하여 산소를 액화하였다. 압축기의 효율을 70%로 가정하였으며 Table 4에는 Linde-Hampson 사이클에 의한 산소액화공정에 대한 전산 모사 결과를 요약하여 정리하였다. Table 4에 의하면 2기의 압축기의 총 소요 동력은 64,873.9 kW인 것을 알 수 있다. 이는 Table 3에서 산소의 부피 유량이 10,000 Nm3/h이므로 이를 질량 유량으로 환산하면 14.2857 ton/h가 된다. 따라서 산소 1 ton 당 액화를 위한 소요 동력은 4,541.2 kW가량 소요되는 것으로 전산모사 결과로 얻을 수 있었다.
3.2 Claude 사이클에 의한 산소액화공정의 전산 모사
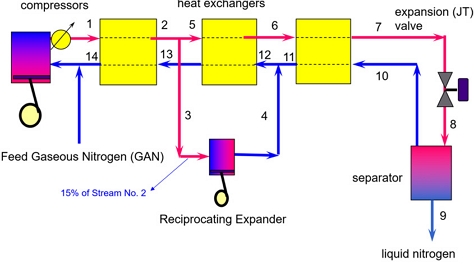
Fig. 3에는 Claude 사이클에 의한 산소액화공정에 대한 개념도를 나타내었다. Fig. 3에 의하면 Claude 사이클에서는 Linde-Hampson 사이클과 다른 것은 산소기체의 일부인 약 15%가량을 팽창기를 통해서 더욱 저온을 얻는 것과 동시에 동력을 생산하는 것이다. 그리고 저온의 산소기체와 원료 기체를 2기의 열교환기를 통해서 열을 회수하기 때문에 압축기 소요 동력을 더욱 줄일 수 있다는 장점이 있다.
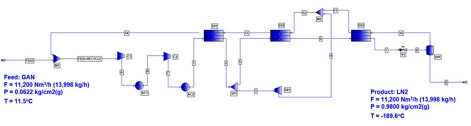
Fig. 4에는 Claude 사이클에 대한 PRO/II를 이용한 산소액화공정에 대한 flow sheet를 나타내었다. Fig. 4에 의하면 Claude 사이클에 의한 산소액화공정은 중간에 냉각기를 가지는 2기의 압축기를 사용하여 산소를 액화하였으며, 산소기체의 일부를 터보 팽창기를 이용하여 동력을 생산함과 동시에 더욱 저온의 산소기체를 얻을 수 있도록 하였다. 한편 차가운 산소기체와 원료 기체 사이의 열교환기의 수를 3기로 늘려서 저온의 열의 회수를 극대화시켰다.
Table 5에는 Claude 사이클에 의한 산소액화공정에 대한 전산 모사 결과를 요약하여 정리하였다. Table 5에 의하면 2기의 압축기의 총 소요 동력은 26,279.8 kW인 것을 알 수 있다. 이는 Table 4에 요약하여 정리한 Linde-Hampson 산소액화공정에 필요한 소요 동력이 64,873.9 kW인 것에 비해서 약 40.49%가량으로 줄어든 것을 알 수 있다. 1 ton 당 액화를 위한 소요 동력은 터보 팽창기를 통해서 얻은 동력까지 감안하면 3,224.6 kW가량 소요되는 것으로 전산모사 결과로 얻을 수 있었다. 이는 Linde-Hampson 사이클에 의한 질소액화공정에 비해서 약 40.49%가량으로 소요 동력이 줄어드는 것을 알 수 있었다.
4. 결 론
본 연구에서는 산소의 액화를 위해서 Linde-Hampson의 액화공정과 Claude의 액화공정을 적용하여 산소의 액화에 필요한 소요 동력을 전산 모사를 통해서 비교하는 연구를 수행하였다. 그 결과 다음과 같은 결론을 얻을 수 있었다.
첫째, 산소 액화를 위한 Linde-Hampson 사이클에서는 중간에 냉각기를 가지는 2단 압축공정과 2단 압축기 후단에 냉각기를 두었으며, Joule-Thomson 팽창 후에 액화되지 않는 저온의 산소기체와 비교적 고온의 산소기체와의 열교환기를 설치한 공정에 의해서 액화된 공정에 대한 전산모사를 수행하였다. 그 결과 액화된 산소 1 ton 당 소요되는 압축기의 총 소요 동력은 4,544.3 kWh/ton LO2인 것을 알 수 있었다.
둘째, 산소 액화를 위한 Claude 사이클에서는 Linde 사이클과는 달리 터보 팽창기를 사용하였는데 이를 통해서 더욱 저온의 산소기체를 얻을 수 있었으며, 일부 동력 생산을 통해서 산소 액화에 필요한 총 소요 동력을 절감할 수 있었다. 산소 액화에 필요한 동력은 1,775.7 kWh/ton LO2로써 Claude 사이클에 비해서 약 59.51%의 소요 동력을 절감할 수 있었다.
Acknowledgments
이 논문은 2020년도 동양대학교 학술연구비의 지원으로 수행되었다.
References
- J. M. Smith, H. C. Van Ness, M. M. Abbott, and M. T. Swihart, “Introduction to chemical engineering thermodynamics”, 8th ed, McGraw-Hill Higher Education, USA, 2018, pp. 1-4.
- S. I. Sandler, “Chemical, biochemical, and engineering thermodynamics”, 4th ed, John Wiley & Sons, Inc., USA, 2006, pp. 4-5.
- J. H. Cho, “Energy saving through process improvement, CO2 capture and unutilized energy utilization technology”, A-JIN, Korea, 2018, pp. 165-178.
- J. H. Cho, J. G. Park, and S. T. Kim, “Simulation of chemical process using Pro/Ⅱ with PROVISION”, A-JIN, Korea, 2004, pp. 49-61.
-
G. Soave, “Equilibrium constants from a modified Redlich-Kwong equation of state”, Chem. Eng. Sci., Vol. 27, No. 6, 1972, pp. 1197-1203.
[https://doi.org/10.1016/0009-2509(72)80096-4]

-
D. Y. Peng and D. B. Robinson, “A new two-constant equation of state”, Ind. Eng. Chem. Fundamen., Vol. 15, No. 1, 1976, pp. 59-64.
[https://doi.org/10.1021/i160057a011]

-
G. M. Kontogeorgis and G. K. Folas, “Thermodynamic models for industrial applications: from classical and advanced mixing rules to association theories”, John Wiley & Sons, Inc., USA, 2009, pp. 41-42.
[https://doi.org/10.1002/9780470747537]

- K. E. Starling and Y. C. Kwok, “Fluid thermodynamic properties for light petroleum systems”, Hydrocarbon Process., Vol. 50, No. 4, 1971, pp. 140.
- O. Kunz, R. Klimeck, W. Wagner, and M. Jaeschke, “The GERG-2004 wide-range equation of state for natural gases and other mixtures”, Association of German Engineers, 2007. Retrieved from https://www.gerg.eu/wp-content/uploads/2019/10/TM15.pdf, .
-
C. H. Twu, D. Bluck, J. R. Cunningham, and J. E. Coon, “A cubic equation of state with a new alpha function and a new mixing rule”, Fluid Phase Equilib., Vol. 69, 1991, pp. 33-50.
[https://doi.org/10.1016/0378-3812(91)90024-2]