[ Article ]

Transactions of the Korean Hydrogen and New Energy Society - Vol. 31, No. 1, pp.112-121

ISSN: 1738-7264 (Print) 2288-7407 (Online)

Print publication date 28 Feb 2020

Received 30 Jan 2020 Revised 24 Feb 2020 Accepted 28 Feb 2020

DOI: https://doi.org/10.7316/KHNES.2020.31.1.112

열교환기 형식에 따른 열교환기의 에너지 및 엔트랜시 성능 특성 해석

김경훈¹ ; 정영관¹ ; 한철호²^{, †}

1금오공과대학교 기계공학과
2금오공과대학교 기계시스템공학과

Energy and Entransy Characteristic Analysis of Heat Exchangers Depending on Heat Exchanger Type

KYOUNG HOON KIM¹ ; YOUNG GUAN JUNG¹ ; CHUL HO HAN²^{, †}

1Department of Mechanical Engineering, Kumoh National Institute of Technology, 61 Daehakro, Gumi 39177, Korea
2Department of Mechanical System Engineering, Kumoh National Institute of Technology, 61 Daehakro, Gumi 39177, Korea

Correspondence to: ^† chhan@kumoh.ac.kr

Abstract

In this work energy and entransy characteristics of heat exchangers are analyzed for 12 different flow arrangements of heat exchangers. The dimensionless parameters are number of entransy dissipation (Ng), number of entransy dissipation-based thermal resistance (Nr), and entransy dissipation-based effectiveness of heat-exchanger (εg). The dimensionless parameters are expressed analytically in terms of the effectiveness of heat exchanger (ε), heat capacity ratio (c), and number of transfer unit (N) for optimal performance of heat exchangers. Results showed that the dimensionless parameters based on the entransy dissipation can be useful concepts for optimal design of heat exchangers.

Keywords:

Heat exchanger, Energy, Entransy, Effectiveness, Number of transfer unit(NTU), Entransy dissipation

키워드:

열교환기, 에너지, 엔트랜시, 유용도, 전달단위수, 엔트랜시 소산

1. 서 론

Guo 등¹⁾에 의해 제안된 엔트랜시(entransy) 개념은 열과 전기 전도 사이의 새로운 상사량이다. 엔트랜시는 축전기의 전기적 포텐셜 에너지에 상응해서 열전달 능력에 해당되며 열적 포텐셜 에너지를 나타낸다. 열전달 과정에서 발생한 손실인 엔트랜시 소산(entransy dissipation)은 열전달의 비가역성을 나타내며^2,3), 비가역 열전달 과정이나 열교환기와 에너지 시스템의 최적설계의 해석에 유용하다^4-7).

Qian과 Li⁸⁾는 다양한 열교환기의 해석을 위해 엔트랜시 소산에 기반한 열저항 무차원수(number of entransy-dissipation- based thermal resistance, N_r)를 제안하였다. 그들은 최소 엔트로피 생성에 의한 설계가 최대 열전달 설계와 항상 연결되는 것은 아니라고 보고하였다. Cheng 등⁹⁾은 엔트랜시 소산에 기반한 다통로 열교환기에 관한 연구를 통해 Nr의 최소값은 열교환기의 최적 성능에 일치한다고 보고하였다. Wu와 Cheng¹⁰⁾은 다차원 정상상태 시스템을 위한 일반화된 열저항 개념을 정의하기 위해 열복사 문제들에 엔트랜시 소산 열저항수 N_r에 기반한 방법을 도입하였다.

Chen¹¹⁾은 평행류, 대향류, TEMA E-type 다관통식 열교환기에서 N_r의 개념이 열교환기 종류나 열용량, 열전도율 등이 열교환기 성능에 잘 연결된다고 보고하였다. Wang 등¹²⁾은 수치적인 방법으로 기하학적 계수들이 N_r에 미치는 영향을 조사하였다. 그들은 나선형 열교환기에서 Nr을 최적설계의 목적함수로 사용하는 것이 전통적인 방법보다 장점이 있다고 보고하였다.

Xu 등¹³⁾은 열교환기 네트워크(heat exchanger network, HEN)의 최적설계의 제한조건에 엔트랜시 균형방정식을 도입하면 방정식의 숫자가 줄고 해가 간단해짐을 보였다. Xia 등¹⁴⁾은 열교환기 네트워크 해석에 엔트랜시 이론에 기반한 T-Q 선도 도입을 제안하였으며 엔트랜시 전달 효율(entransy transfer efficiency)을 통해 에너지가 절감될 수 있는 포텐셜을 보였다. Hua 등¹⁵⁾은 비정상 최적설계 문제에 엔트랜시 이론을 확장시켰다. Wen 등¹⁶⁾은 엔트랜시 이론과 유전자 알고리즘을 결합한 최적화 전략을 제안하였으며, 다관통식 열교환기에 엔트랜시 이론이 적용될 수 있음을 보였다.

그러나 아직 다양한 열교환기 종류에 대해 전통적인 무차원수와 엔트랜시 소산에 기반한 무차원수의 관계에 대한 연구 보고가 매우 부족한 실정이다. 본 논문에서는 많이 사용되는 12가지 종류의 열교환기에 대해서 전통적인 무차원수와 엔트랜시 소산에 기반한 무차원수들을 비교 해석한다. 무차원 계수들은 열교환기유용도, 열용량비(heat capacity ratio) 및 전달단위수(number of transfer unit (NTU or N)의 항으로 수학적으로 유도하고 중요한 특성을 분석한다.

2. 시스템 해석

2.1 에너지, 엔트로피, 엔트랜시 해석

열교환기에 고온과 저온 유동이 있으며 고온유동과 저온유동의 열용량을 각각 C_h = m_hc_ph 및 C_c = m_cc_pc라 한다. 여기에서 m과 c_p는 각각유동의 질량유량과 정압비열이고 하첨자 h와 c는 각각 고온유동과 저온유동을 의미한다. 열교환기는 하나의 검사체적이며 열교환기의 외부표면이나 주위로의 열전달은 없다고 가정한다. 열교환기 내 유체 유동에 의한 압력강하는 열전달 효과보다 작기 때문에 무시한다. 그러면 열교환기 내 에너지 균형식은 다음과 같이 쓸 수 있다.

Q = C h T h i - T h o = C c T c o - T c i = ε C min T h i - T c i

(1)

여기에서 Q는 고온과 저온 유체사이의 열전달, T는 절대온도, C_min은 C_h와 C_c 중 최소 열용량, ε은 열교환기 유용도 그리고 하첨자i와 o는 각각 입구와 출구를 의미한다. 그러면 고온과 저온 유체의 출구온도 T_ho와 T_co는 다음과 같이 구한다.

T h o = T h i - Q / C h

(2)

T c o = T c i + Q / C c

(3)

열용량과 온도 조건들이 규정된 경우에 이와 같은 임무를 달성하기 위한 열교환기의 크기는 아직 결정된 것이 아니다. 열교환기의 크기는 다음과 같은 열전달식으로부터 구할 수 있다:

Q = U A ∆ T m

(4)

여기에서 A, U 및 UA는 각각 고온이나 저온측 열교환면적, 총괄열전달계수(overall heat transfer coefficient)와 열전도율(thermal conductance)을 의미한다.

ΔT_m은 고온과 저온유체 사이의 평균온도차로서 ΔT_m= Q/(UA)로 정의된다. 평행류와 대향류 열교환기에서 평균온도차는 다음과 같은 로그평균온도차(logarithmic mean temperature difference, LMTD)로 표현된다:

∆ T m, c f = T h i - T c o - T h o - T c i ln ⁡ T h i - T c o T h o - T c i

(5)

∆ T m, p f = T h i - T c i - T h o - T c o ln ⁡ T h i - T c i T h o - T c o

(6)

여기에서 하첨자 pf와 cf는 각각 평행류와 대향류를 의미한다.

열전달 관계식들을 열저항의 항으로 표현하면 1계 열시스템의 해석을 간단하게 해준다. 열전달 Q가 전류와 상사하고 온도차 ΔT가 전압차와 상사하다는 사실을 상기하면 열저항 R은 다음과 같이 정의할 수 있다:

R = ∆ T / Q

(7)

엄밀하게 말하자면 이러한 상사는 열전도에 국한되기는 하지만 이러한 표현을 열전달 전체 모드로 확장할 수 있다.

Guo 등¹⁾은 열전달 과정을 연구할 수 있는 물리량으로서 엔트랜시를 다음과 같이 정의하였다.

G = 12 U T

(8)

여기에서 U는 내부에너지이다. 열전달 과정 중 엔트랜시는 전달되는 과정에 일부가 소산되며, 이는 전기전도 과정에서 전기에너지의 경우와 마찬가지이다¹¹⁾. 엔트랜시 소산은 다음과 같이 정의할 수 있다:

G d = 12 C h T h i 2 - T h o 2 - 12 C c T c o 2 - T c i 2 = C h T h i - T h o T h i + T h o 2 - C c T c o - T c i T c i + T c o 2 = Q T h i + T h o 2 - T c i + T c o 2 = Q ∆ T g

(9)

여기에서 ΔT_g는 엔트랜시 소산에 기반한 열교환기내 평균온도차로서 다음과 같이 정의된다.

∆ T g = G d Q = T h i + T h o 2 - T c i + T c o 2

(10)

엔트랜시 소산 G_d는 식 (2)와 (3)으로부터 다음과 같이 유도된다:

G d = Q T h i - T c i - 1 + c 2 C min Q 2

(11)

여기에서 c = C_min/C_max는 열용량비이며 C_max는 C_h 와 C_c 중 큰 것이다.

엔트랜시 소산 기반 열저항(entransy dissipation- based thermal resistance, EDTR), R_g는 Xia 등¹⁴⁾에 의해 열전문제의 최적화 연구를 위해 처음 정의되었다:

R g = G d Q 2 = 1 C min 1 ε - 1 + c 2

(12)

엔트랜시 소산 열저항의 개념을 이용한 최소열저항 정리는 열전도 문제의 최적화 연구를 위해 도입되었으며 최소 엔트로피 생성원리에는 없는 장점이 존재한다¹⁴⁾.

2.2 무차원계수

서로 다른 입구 온도 조건이나 열용량비로 운전되는 열교환기의 성능을 비교하기 위해서는 무차원 계수들이 필요하다. 무차원 엔트랜시 소산수 N_g는 다음과 같이 정의한다:

N g = G d 12 C min T h i - T c i 2

(13)

그러면 이것은 (11)식과 (13)식을 이용하여 유용도와 열용량비의 함수로 다음과 같이 나타낼 수 있다:

N g = 2 ε - 1 + c ε 2

(14)

무차원 계수인 엔트랜시소산 저항수 N_r은 다음과 같이 정의된다.

N r = C min R g

(15)

이는 유용도와 열용량비의 항으로 (12)와 (15)식을 이용하여 다음과 같이 쓸 수 있다:

N r = 1 ε - 1 + c 2

(16)

엔트랜시는 열전달 능력을 나타내기 때문에 무차원수 엔트랜시 소산 유용도 ε_g를 다음과 같이 정의할 수 있다:

ε g = 1 U A R g

(17)

그러면 이는 식 (4), (12)와 (17)을 이용하여 다음과 같이 유용도와 열용량비의 항으로 나타낼 수 있다:

ε g = Q 2 U A G d = Q U A ∆ T g = ∆ T m ∆ T g = 1 N 1 ε - 1 + c 2

(18)

여기서 N은 전달단위수(the number of transfer unit)로서 N = UA/C_min와 같이 정의된다.

2.3 열교환기 형태에 따른 해석

지금까지 엔트로피 생성수 N_s, 엔트랜시 소산수 N_g, 엔트랜시소산 저항수 N_r 및 엔트랜시소산 유용도ε_g 등의 무차원수들은 N과 c의 항으로 표시됨을 보았다. 각 열교환기에서 유용도는 다음과 같이 N과 c의 항으로 표시된다¹⁷⁾.

1) counter flow:

ε N, c = 1 - exp - 1 - c N 1 - c exp - 1 - c N

(19)

2) parallel flow:

ε N, c = 1 - exp - 1 + c N 1 + c

(20)

3) cross flow, both fluids unmixed:

ε N, c = 1 - exp N 0.22 c exp - c N 0.78 - 1

(21)

4) cross flow, both fluids mixed:

ε N, c = 1 1 1 - exp - N + c 1 - exp - c N - 1 N

(22)

5) cross flow, C_min = unmixed, C_max = mixed:

ε N, c = 1 - exp - c 1 - exp - N c

(23)

6) cross flow, C_min = mixed, C_max = unmixed:

ε N, c = 1 - exp - 1 c 1 - exp - c N

(24)

7) TEMA E, 1-2 shell mixed:

ε N, c = 2 1 + c + 1 + c 2 coth ⁡ N 1 + c 2 2

(25)

8) TEMA E, 1-2 shell unmixed, C_min = C_tube:

ε N, c = 1 - 2 c - 1 2 c + 1 2 c + exp - N c + 12 2 c - exp - N c - 12

(26)

9) TEMA E, 1-4 shell mixed, C_min = C_tube:

ε N, c = 4 2 1 + c + 1 + 4 c 2 coth ⁡ N 1 + 4 c 2 2 + tanh ⁡ N 4

(27)

D N, c = 1 - exp - N 2 c + 1 4 2 c + 1

(28)

G N, c = 1 - exp - N 2 c - 1 4 2 c - 1

(29)

F 1 N, c = 1 + G + 2 c G + 2 c + 1 D - 1 exp - N 2 c + 1 4 1 + G + 2 c G + 2 c 1 - D + 2 c D exp - N 2 c + 1 4

(30)

10) TEMA G, 1-2 split shell mixed, C_min = C_tube:

ε N, c = F 1 N, c

(31)

11) TEMA G, 1-2 split shell mixed, C_min = C_shell:

ε N, c = 1 c F 1 c N, 1 c

(32)

12) TEMA J, 1-2 divided shell mixed, C_min = C_tube:

ε N, c = 2 1 + 2 c Φ 1

(33)

γ = 1 + 4 c 2 2 c

(34)

Φ = exp ⁡ - γ c N

(35)

Φ 1 = 1 + γ 1 + Φ 1 - Φ - 2 γ γ Φ + 1 - Φ exp ⁡ - c N γ - 1 2 1 - Φ 2 + γ 1 - Φ 2

(36)

이중에서 특히 type 1 (counter flow), type 2 (parallel flow)와 type 7 (TEMA E, 1-2 shell mixed)에서는 엔트랜시 소산수 N_r과 엔트랜시 소산 유용도ε_g는 다음과 같이 간단하게 표현될 수 있다:

N r = F coth ⁡ F N

(37)

ε g = tanh ⁡ F N F N

(38)

여기에서 F는 다음과 같은 형태계수이다.

F = 1 - c 2 for type1 for counter flow = 1 + c 2 for type2 for parallel flow = 1 + c 2 2 for type7 TEMA E,1-2 shell mixed

(39)

여기서 주목할 것은 식 (39) 형태의 엔트랜시 소산 유용도는 휜 끝에서 열전달이 무시되는 핀 휜의 휜효율과 같다는 점이다.

3. 결과 및 고찰

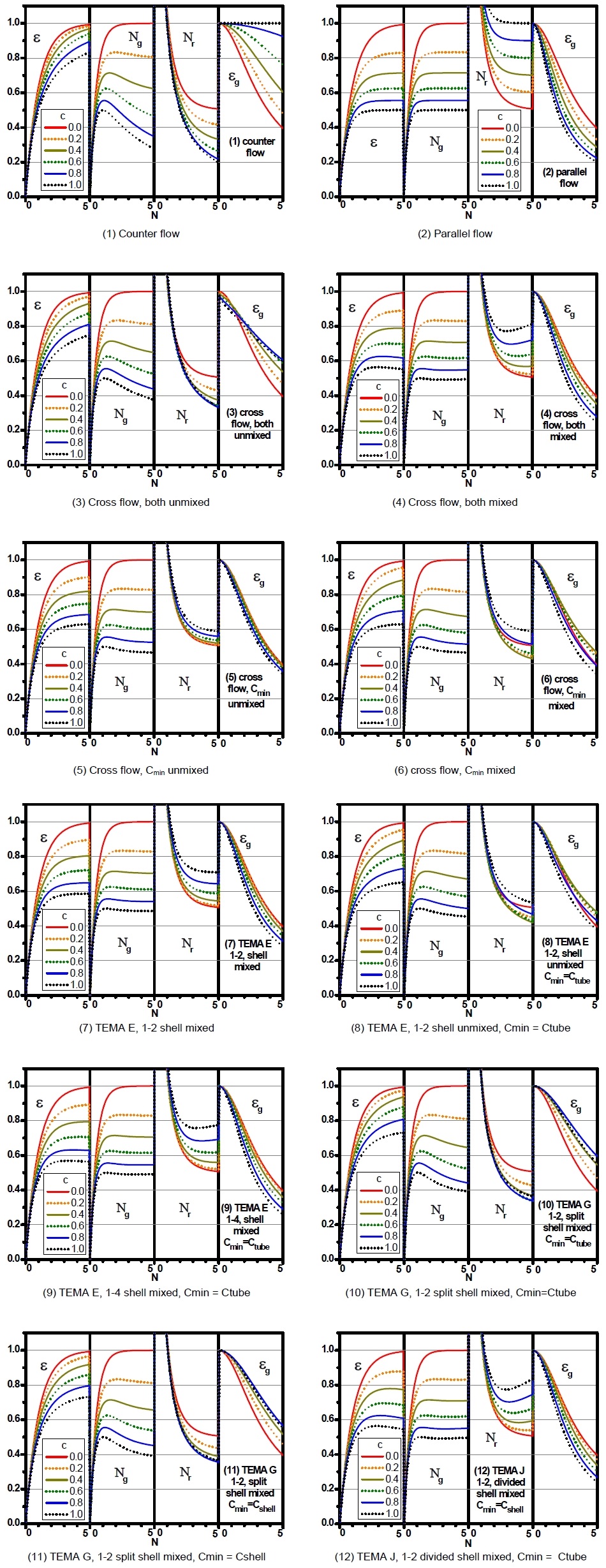
열교환기의 해석을 위해서는 ε-NTU법이 널리 쓰이고 있는데, 엔트랜시 소산에 기반한 계수들도 ε-NTU법과 같은 형태로 분석하고자 한다. Fig. 1은 12종류의 열교환기에 대해 열교환기 유용도 ε와 함께 엔트랜시 소산에 기반한 무차원수들인 인트랜시 소산수 N_g, 엔트랜시 소산 열저항수 N_r, 및 엔트랜시 소산 유용도 ε_g의 거동을 전달단위수 N과 열용량비 c의 함수로 비교해서 보여준다. 우리는 여기에서 전체 열교환기에 적용되는 일반적인 현상들을 찾을 수 있다.

Fig. 1.

Dimensionless parameters with varying N and c

1) 열용량비 c가 0에 가까워지면 모든 종류의 열교환기들에서 무차원수들은 다음과 같은 식들로 수렴한다.

ε = 1 - e - N

(40)

N g = 1 - e - 2 N

(41)

N r = 12 coth ⁡ N 2

(42)

ε g = tanh ⁡ N / 2 N / 2

(43)

2) ε과 N_g는 c가 증가함에 따라 감소한다.

∂ ε ∂ c < 0, ∂ N g ∂ c < 0, ∂ N r ∂ c ∂ ε g ∂ c < 0 for N > 0

(44)

그러나 c에 대한 N_r과 ε_g의 변화는 열교환기 종류와 N에 따라 달라진다. 예를 들어 type 1 (counter flow), type 2 (parallel flow) 및 type 7 (TEMA E, 1-2 shell mixed)에서ε_g는 식 (42)로부터 다음과 같이 유도된다:

ε g = tanh ⁡ z z, z = F N

(45)

여기에서 F는 식 (39)에서 주어지는 열교환기의 형태계수이다. 이식을 c에 대해 미분하면 다음과 같이 됨을 알 수 있다.

∂ ε g ∂ c = d d z tanh ⁡ z z N ∂ F ∂ c

(46)

∂ F ∂ c = - 12 < 0 for counter flow = 12 > 0 for parallel flow = c 2 1 + c 2 > 0 for type7.

(47)

N값과 관계없이 d(tanh(z)/z)/dz < 0 관계가 성립하므로 식 (47)로부터 다음 관계가 성립한다.

∂ ε g ∂ c > 0 for counter flow, ∂ ε g ∂ c < 0 for parallel flow and  type7

(48)

3) N이 0에 접근하면 ε, N_g 및 N_r도 역시0에 접근한다.

ε → 0, N g → 0, N r → ∞ as N → 0

(49)

4) N이 무한대로 커지면 ε, N_g 및 N_r은 유한한 값으로 수렴한다.

ε → ε ∞ 0 ≤ ε ∞ ≤ 1 as N → ∞

(50)

N g → 2 ε ∞ - 1 + c ε ∞ 2 as N → ∞

(51)

N r → 1 ϵ ∞ - 1 + c 2 a s N → ∞

(52)

5) 전달단위수 N이 증가함에 따라 일반적으로 ε은 단순 증가하고 N_r은 단순 감소한다. 그러나 비열비 c값이 클 때 4, 9 및 12 형식 열교환기의 경우에는 ε은 N에 대해 극대값을 가질 수 있고 N_r은 N에 대해 극소값을 가질 수 있으며, 이 경우 식 (14)로부터 ε의 극대값과 N_r의 극소값이 일어나는 N값은 같다는 사실을 알 수 있다.

6) 엔트랜시 소산수 N_g의 전달단위수 N에 대한 미분은 식 (18)로부터 다음과 같이 쓸 수 있다.

∂ N g ∂ N = - 2 1 + c ϵ - 1 1 + c ∂ ϵ ∂ N

(53)

열용량비 c값이 클 때의 4, 9 및 12 타입열교환기를 제외하고 ∂ε/∂N > 0가 되므로, ε < 1/(1+c)인 경우 N_g는 N에 대해 단순 증가하며, 그렇지 않은 경우에는 N에 대해 극소값을 갖는다. c값이 클 때 4, 9 및 12 타입의 경우에는 미분값 ∂ε/∂N이 음의 값을 가지므로 N에 대해 극대값이 존재한다.

7) 모든 종류의 열교환기 종류에서 ε_g는 N에 대해 단조감수하며 N이 0에 접근하면 ε_g는 1에 수렴하고, N이 무한히 커지면 ε_g는 0에 수렴한다. 그러므로 모든 열교환기 종류에 대해 다음 관계가 성립한다:

∂ ε g ∂ N < 0 for 0 < N < ∞

(54)

ε g → 1 as N → 0

(55)

ε g → 0 as N → ∞

(56)

식 (55)의 조건은 다음과 같이 간접적으로도 보일 수 있다. N이 0에 가까워지면 고온과 저온유체의 출구온도는 각각의 입구온도에 가까워지므로 ΔT_m과 ΔT_g 모두 고온 입구온도와 저온 입구온도의 차이 T_hi - T_ci에 수렴하게 되어 식 (18)로부터 ε_g는 1에 수렴한다:

ε g = ∆ T m ∆ T g → T h i - T c i T h i - T c i = 1 as N → 0

(57)

4. 결 론

본 연구에서는 12종류의 열교환기에 대해 엔트랜시 소산을 기반으로 하는 엔트랜시 소산수 N_g, 엔트랜시 소산 저항수 N_r, 엔트랜시 소산 유용도 ε_g와 열교환기 유용도 ε를 비교 해석하였다. 각 열교환기에 대해 무차원 계수들을 전달단위수 N과 열용량비 c의 함수로 수학적으로 유도하고 그 영향을 조사하였다. 주요 결과는 다음과 같다.

일반적으로 N이 증가함에 따라 ε은 단조 감소하고 N_r은 단조 감소하는 반면에 N_g는 만일 ε = 1/(1+c)의 조건을 만족할 수 있으면 극대값을 갖고, 그렇지 못하면 단조 증가한다. 열교환기 4, 9 및 12 타입에서 c의 값이 크면 같은 N값에서 ε은 극대값을 갖고 N_r은 극소값을 갖는다. 모든 종류의 열교환기에서 ε_g는 N에 대해 단조 감소하며, N이 0으로 작아지면 1에 수렴하고 무한히 커지면 0에 수렴한다. 대향류, 평행류 및 7 타입의 열교환기에서 ε_g는 휜효율과 같아진다. ε_g는 Q/(UAΔT_g)로 나타낼 수 있으며 여기에서 ΔT_g = G_d/Q는 고온유체 평균온도와 저온유체 평균온도의 차이다. UA가 커지는 대가로 N_r이 증가하거나 감소할 수 있음을 고려하면 ε_g의 개념은 열교환기 최적설계에 있어서 유용한 개념이 될 수 있다.

Acknowledgments

이 연구는 금오공과대학교 학술연구비로 지원되었습니다(2018-104-123).

References

Z. Y. Guo, H. Y. Zhu, and X. G. Liang, “Entransy – a physical quantity describing heat transfer ability”, Int. J. Heat Mass Transfer, Vol. 50, No. 13-14, 2007, pp. 2545-2556. [https://doi.org/10.1016/j.ijheatmasstransfer.2006.11.034]
X. T. Cheng, X. G. Liang, and Z. Y. Guo, “Entransy decrease principle of heat transfer in an isolated system”, Chin. Sci. Bull., Vol. 56, 2011, pp. 847-854. [https://doi.org/10.1007/s11434-010-4328-4]
X. T. Cheng and X. G. Liang, “From thermomass to entransy”, Int. J. Heat Mass Transfer, Vol. 62, 2013, pp. 174-177. [https://doi.org/10.1016/j.ijheatmasstransfer.2013.02.063]
Z. Q. Yu, P. Wang, W. J. Zhou, Z. Y. Li, and W. Q. Tao, “Study on the consistency between field synergy principle and entransy dissipation extremum principle”, Int. J. Heat Mass Transfer, Vol. 116, 2018, pp. 621-634. [https://doi.org/10.1016/j.ijheatmasstransfer.2017.09.044]
L. Zhang, H. Y. Wei, and X. S. Zhang, “Theoretical analysis of heat and mass transfer characteristics of a counter-flow packing tower and liquid desiccant dehumidification systems based on entransy theory”, Energy, Vol. 141, 2017, pp. 661-672. [https://doi.org/10.1016/j.energy.2017.09.118]
K. H. Kim and K. Kim, “Comparative analyses of energy–exergy–entransy for the optimization of heat-work conversion in power generation systems”, Int. J. Heat Mass Transfer, Vol. 84, 2015, pp. 80‒90. [https://doi.org/10.1016/j.ijheatmasstransfer.2015.01.002]
C. H. Han and K. H. Kim, “Entransy and exergy analyses for optimizations of heat-work conversion with carnot cycle”, J. Ther. Sci., Vol. 25, 2016, pp. 242-249. [https://doi.org/10.1007/s11630-016-0856-9]
X. Qian and Z. Li, “Analysis of entransy dissipation in heat exchangers”, Int. J. Thermal Sci., Vol. 50, No. 4, 2011, pp. 608-614. [https://doi.org/10.1016/j.ijthermalsci.2010.11.004]
X. Cheng, Q. Zhang, and X. Liang, “Analyses of entransy dissipation, entropy generation and entransy–dissipation-based thermal resistance on heat exchanger optimization”, App. Therm. Eng., Vol. 38, 2012, pp. 31-39. [https://doi.org/10.1016/j.applthermaleng.2012.01.017]
J. Wu and X. Cheng, “Generalized thermal resistance and its application to thermal radiation based on entransy theory”, Int. J. Heat Mass Transfer, Vol. 58, No. 1-2, 2013, pp. 374-381. [https://doi.org/10.1016/j.ijheatmasstransfer.2012.11.046]
Q. Chen, “Entransy dissipation-based thermal resistance performance design and optimization”, Int. J. Heat Mass Transfer, Vol. 60, 2013, pp. 156-162. [https://doi.org/10.1016/j.ijheatmasstransfer.2012.12.062]
S. Wang, G. Jian, J. Wang, L. Sun, and J. Wen, “Application of entransy-dissipation-based thermal resistance for performance optimization of spiral-wound heat exchanger”, Int. J. Heat Mass Transfer, Vol. 116, 2018, pp. 743–750. [https://doi.org/10.1016/j.ijheatmasstransfer.2017.09.061]
Y. C. Xu, Q. Chen, and Z. Y. Guo, “Optimization of heat exchanger networks based on Lagrange multiplier method with the entransy balance equation as constraint”, Int. J. Heat Mass Transfer, Vol. 95, 2016, pp. 109–115. [https://doi.org/10.1016/j.ijheatmasstransfer.2015.11.092]
L. Xia, Y. Feng, X. Sun, and S. Xiang, “A novel method based on entransy theory for setting energy targets of heat exchanger network”, Chinese Journal of Chemical Engineering, Vol. 25, No. 8, 2017, pp. 1037–1042. [https://doi.org/10.1016/j.cjche.2017.03.015]
Y. C. Hua, T. Zhao, and Z. Y. Guo, “Optimization of the one-dimensional transient heat conduction problems using extended entransy analyses”, Int. J. Heat Mass Transfer, Vol. 116, 2018, pp. 166–172. [https://doi.org/10.1016/j.ijheatmasstransfer.2017.08.101]
J. Wen, X. Gu, M. Wang, Y. Liu, and S. Wang, “Multi-parameter optimization of shell-and-tube heat exchanger with helical baffles based on entransy theory”, Applied Thermal Engineering, Vol. 130, 2018, pp. 804–813. [https://doi.org/10.1016/j.applthermaleng.2017.10.164]
A. Bejan and A. D. Kraus, “Heat transfer handbook”, John Wiley & Sons, USA, 2003.