프란시스 수차 모델의 러너 간극에 따른 내부유동 및 성능 특성
2020 The Korean Hydrogen and New Energy Society. All rights reserved.
Abstract
In the Francis turbine, the leakage flow through the runner gaps which are between the runner and the stator structure influences the internal flow and hydraulic performance. Thus, the investigation for the flow characteristics induced by the runner gaps is important. However, the runner gaps are often disregarded by considering the time and cost of the numerical analysis. Therefore, in this study, the flow characteristics according to runner gaps of the Francis turbine model were investigated including the leakage flow of the runner cone. The three-dimensional unsteady Reynolds-averaged Navier-Stokes analyses were conducted using a scale-adaptive simulation shear stress transport as a turbulence model for observing the influence of the leakage flow on the internal flow and hydraulic performance. The efficiencies were decreased slightly with runner gaps; and the complicated flows were captured in the gaps.
Keywords:
Francis turbine, Runner gap, Leakage flow, Numerical analysis키워드:
프란시스 수차, 러너 간극, 누설 유동, 수치해석1. 서 론
최근 수치해석을 적용한 연구 분야가 현저히 증가하고 있으며, 보다 정확한 수치해석을 통한 성능 예측 및 유동 검토를 위해 해석 대상이 되는 물리적 모델 및 조건을 정확히 반영하는 것이 중요하다. 하지만 일반적으로 수치해석의 목적, 시간 및 비용을 고려하여 복잡한 구조의 모델을 단순화 및 이상적인 조건으로 가정하여 해석을 수행한다.
한편, 프란시스 수차는 회전자인 러너와 고정자 구조물 사이에 전형적인 비접촉 유형의 라비린스 실이 통상 구성되어 있다1,2). 이러한 러너 내 라비린스 실과 같은 간극을 통해 누설 유동이 유발되며, 이는 수차의 수력학적 성능 및 하류의 유동에 영향을 준다3). 하지만 복잡한 유동 구조를 가지는 러너 간극은 프란시스 수차의 주요 구성요소에 비해 상대적으로 매우 작은 구조로써 유동 구조 도메인의 단순화를 위해 종종 고려되지 않는다. 따라서 정확하고 효율적인 수치해석의 대상 범위 선정 및 수행을 위해 수차의 수력학적 성능 및 내부 유동 특성에 대해 러너 간극이 미치는 영향에 대한 검토는 필요하다.
프란시스 수차의 라비린스 실 및 누설 유동이 여러 연구들을 통해 분석되었다. Zhao 등1)은 실의 누설 유동에 대해 실의 공간인 캐비티의 형상 및 수에 따른 영향을 수치해석적으로 분석하였고, Čelič와 Ondráčka2)는 프란시스 수차의 라비린스 실의 손실이 수력학적 효율에 미치는 영향에 대해 수치해석 및 실험을 통해 검토하였으며, Feng 등3)은 프란시스 수차의 성능 및 동익과 정익의 상호 작용(rotor-stator interaction)에 대한 원판 마찰 손실 및 누설 유동의 영향을 연구하였다. 이와 같이 라비린스 실과 같은 러너 간극 및 누설 유동에 대한 여러 연구들이 수행되었지만, 프란시스 수차의 러너 간극뿐만 아니라 러너 콘 내 누설유동을 고려한 성능 및 내부 유동 특성에 대한 분석은 아직 부족하며, 이에 대한 체계적인 분석은 필요하다.
본 연구에서는 프란시스 수차 모델의 러너 간극 및 콘 내 누설 유동에 대한 특성 검토를 위해 삼차원 비정상상태 Reynolds-averaged Navier-Stokes (RANS) 수치해석을 수행하였다. 수치해석은 프란시스 수차 모델의 최고효율점(best efficiency point, BEP) 및 인근 유량 조건에서 수행되었으며, 간극의 고려 여부에 따른 성능 및 내부유동 특성의 비교 분석을 통해 간극에 대한 영향을 규명하고자 하였다.
2. 수치해석 기법
본 연구에서는 본 연구진에 의해 이전 연구에서 수행된 비속도 270급 프란시스 수차 모델을 해당 연구의 기본 모델로 선정하였으며4), 주요 제원은 Table 1에 나타냈다. 여기서 회전속도, 유량 및 에너지는 IEC 60193 규격에서 제시된 계수를 사용하였다5).
프란시스 수차 모델의 비압축성 내부 유동장에 대한 비정상 상태 수치해석 수행을 위해 ANSYS 사(Canonsburg, PA, USA)의 상용 소프트웨어인 ANSYS CFX 19.1을 사용하였다6). Turbo-grid, ANSYS Meshing 및 ICEM-CFD를 사용하여 도메인의 격자를 생성하였고, CFX-Pre를 사용하여 경계 조건을 설정하였으며, CFX-Solver 및 CFX-Post를 사용하여 유동해석의 수행 및 결과를 분석하였다.
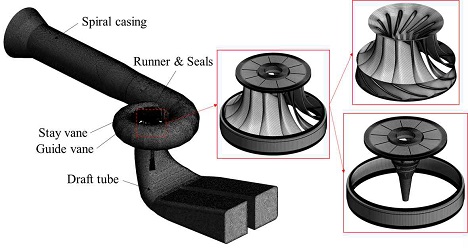
Fig. 1은 프란시스 수차 모델의 격자 구성을 나타내며, 스파이럴 케이싱(spiral casing, SC), 흡출관 및 러너 콘 내 유동 구조는 사면체(tetrahedral) 격자로 이루어져 있고, 그 외의 구성요소 및 러너 간극은 육면체(hexahedral) 격자계로 작성되었다. 러너 블레이드 표면 인근에는 O형 격자계를 사용하여 y+≤5를 유지하도록 하였다. 간극을 제외한 최적 격자계의 격자수는 약 14.74×106개로, grid convergence index (GCI) 방법을 사용하여 선정하였으며, 효율에 대한 는 약 0.0022로 매우 낮은 이산화 오류값으로 Table 2와 같이 계산되었다4,7-9). 러너 간극 및 콘 내 유동 구조에 대한 총 격자수는 약 6.54×106개로 최소 간격에 15개의 격자층을 적용하여 작성하였다. 따라서 러너 간극이 포함된 전체 해석 도메인의 총 격자수 약 21.28×106개를 사용하여 비정상 상태 수치해석을 수행하였다.
한편 본 연구에 적용된 러너 간극의 유동 구조에서 최소 간격은 허브 및 슈라우드에서 각각 약 0.000403D2 및 0.000461D2 값을 나타냈으며, D2는 러너의 출구직경이다.
수치해석을 위한 경계조건으로 프란시스 수차 모델의 입구 및 출구는 각각 전압력 및 정압력 조건을 부여하였다. 난류 모델은 유동 박리에 대한 정확한 예측을 나타내는 scale-adaptive simulation shear stress transport (SAS-SST) 모델을 사용하였으며, 회전자와 고정자 사이의 경계조건은 transient rotor-stator 조건을 사용하였다. 비정상 상태 수치해석을 위한 total time은 총 러너 8회전의 시간인 0.4364s를 적용하였고, time step은 러너의 1.5° 회전 간격인 0.0002272s를 적용하였다. 수치해석의 수렴도를 높이기 위해 loops coefficient는 5로 설정하였다. 본 연구에서는, 비정상 상태 수치해석을 통한 시간에 따른 유동해석 결과 분석을 위해 수치해석의 초기 노이즈를 회피를 위한 러너 5회전 뒤 마지막 3회전에의 결과 값에 대해 시간 평균(time-averaged, Trnavg)하여 분석하였다.
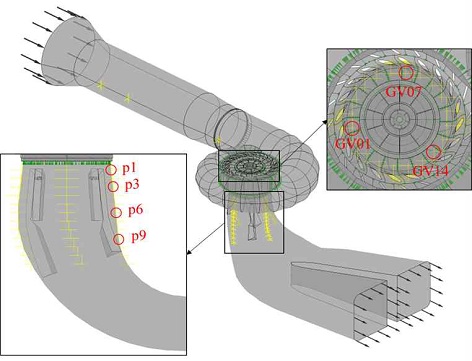
또한, 프란시스 수차 모델의 러너 간극에 따른 내부 유동에 의해 발생하는 비정상 압력 특성을 확인하기 위해 Fig. 2와 같이 가이드 베인(guide vane, GV) 출구(GV01, 07, 14) 및 흡출관 벽면(p1, p3, p6, p9)에 압력 측정점을 적용하여, 비정상 압력 특성을 검토하고자 하였다.
3. 결 과
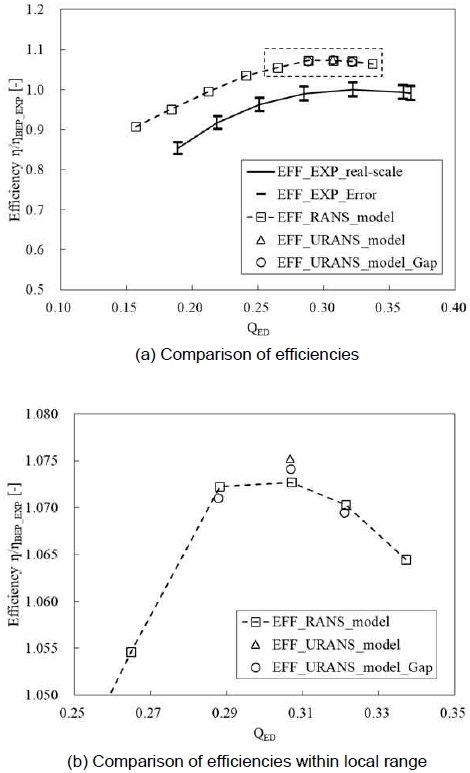
Fig. 3은 수치해석 결과에 대한 타당성을 검토하기 위해 프란시스 수차 모델(model)의 정상 및 비정상 상태 RANS 해석 결과와 실물 수차(real-scale)의 시험 결과를 비교하였다. 실물 수차의 성능시험은 단식압력시간법으로 수행된 수차 효율 시험으로, 측정오차는 ±1.74%이다10). 모델 수차의 효율에 대해 IEC 60193 규격의 효율 환산 공식을 적용하여 실물 수차의 효율과 비교를 하였으며, 식 (1)을 사용하여 계산하였다5). 모델 수차의 효율에서 상사에 따른 손실 효율을 고려하는 효율 환산 공식은 식 (2) 및 (3)을 사용하였다.
| (1) |
| (2) |
| (3) |
여기서 P와 M은 각각 실물과 모델 수차를 의미하며, Reref=7×106, Vref=0.7이다5). 환산된 모델 수차 및 실물 수차의 효율 곡선이 약간의 차이를 나타내지만, 이는 모델 수차의 수치해석에서 실물 수차에서서 발생하는 기계적 손실과 표면 조도 조건 등이 고려되지 않아 발생한 차이로 볼 수 있다. 따라서 모델 및 실물 수차의 효율의 차이는 존재하지만 경향이 전반적으로 유사하므로, 본 연구의 수치해석 결과의 타당성을 확인할 수 있다. 한편, 러너 간극이 적용됨에 따라 전반적으로 효율이 약간 감소하였다(Fig. 3[b]). 비정상 상태 해석을 통한 유동 해석 결과에서는 러너 간극이 적용되었을 때 BEP 조건(QED=0.30)에서 효율이 약 0.1% 감소하였다.
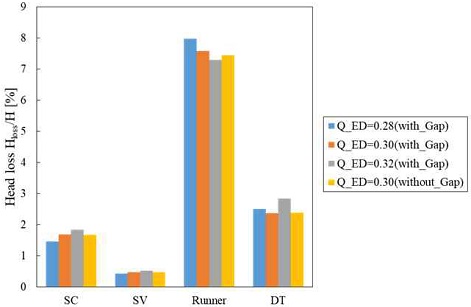
러너 간극에 따른 수차의 성능 특성에 대한 검토하기 위해, Fig. 4와 같이 프란시스 수차 모델의 각 구성요소에 대한 head 손실을 계산하였다. 프란시스 수차 모델의 SC, 스테이 베인(stay vane, SV), GV 및 흡출관(DT)은 식 (4)를 사용하였고, 러너의 head 손실은 식 (5)를 사용하여 계산하였다.
| (4) |
| (5) |
여기서 Δptotal, ρ, g, T, ω 및 Q는 각각 구성요소의 전압력 차, 물의 밀도, 중력 가속도, 러너의 토크, 각속도 및 유량을 나타낸다. 러너 간극이 적용되었을 때 각 구성요소의 head 손실은 유량에 따라 달라지는 특성을 나타냈으며, 동일한 유량 조건인 QED=0.30에서 러너 간극에 따라 각 구성요소에서 유사한 head 손실을 나타냈지만, 러너에서 약 0.15%로 가장 큰 차이를 나타냈다.
Fig. 5는 평면(Fig. 5[a])에서의 시간 평균된 압력분포를 나타내고 있으며, 압력은 최고 압력값으로 무차원화 하였다. 압력분포는 유량에 따라 전반적으로 조금 다른 분포를 나타내고 있으며, 러너 콘 내 유동 특성이 달라지는 것을 볼 수 있다. 또한, 슈라우드 간극의 입구 면적이 상대적으로 매우 좁아 인근에서 복잡한 유동을 유발하기 때문에 간극 입구의 압력이 상대적으로 증가하는 것을 볼 수 있다. 이와 같이 러너 및 콘 내 간극으로 통과하는 누설 유동이 프란시스 수차의 누설 손실로 작용한다.
Fig. 6은 Fig. 5(a)의 평면에서 점선으로 표시된 허브 및 슈라우드 간극 영역에서의 시간 평균된 유선 속도 분포를 나타내며, 속도는 최고 속도로 무차원화 하였다. 관찰된 유량 조건들에서 모두 복잡한 내부유동을 나타낸다. 이렇게 러너 간극으로 유입되는 유동은 러너의 유량 손실로 작용하며, 러너의 유동 특성에 영향을 줄 수 있다.
러너 간극을 통한 누설 유동으로 인해 러너의 유동에 미치는 영향을 검토하기 위해 BEP 조건에서 러너의 스팬 방향인 허브 (0)부터 슈라우드 (1)까지 전연(leading edge) 및 후연(trailing edge)에서의 시간 평균된 자오선 속도를 Fig. 7과 같이 나타냈다. 여기서 자오선 속도는 최고 속도로 무차원화 하였다. 전연에서는 허브 인근에서 러너 간극에 따라 약간의 속도 차이를 나타내며, 후연에서는 스팬 방향 약 0.2-1.0까지 러너 간극에 따라 약간의 속도 차이를 나타내고 있다. 따라서 Fig. 6에서 관찰된 러너 간극을 적용함에 따라 발생하는 러너의 유량 손실이 러너의 내부 유동 특성에 영향을 주는 것을 알 수 있다.
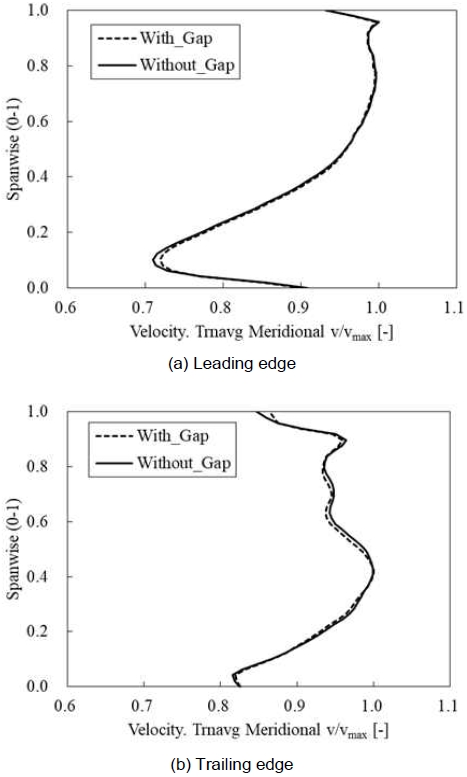
Time-averaged meridional velocity distributions at the leading and trailing edges of the runner at QED=0.30 (best efficiency point)
Figs. 8 및 9는 러너 간극에 대한 영향 범위를 검토하기 위해 러너의 하류 영역인 흡출관 내 축 방향 및 원주 방향 속도 분포를 나타낸다. 흡출관 내 관찰 위치는 Fig. 2에 나타낸 p1 및 p3 높이에서 흡출관 직경 길이에 대해 속도 분포를 검토하였다. 여기서 가로 축은 흡출관의 벽면 (0)부터 벽면 (1)까지의 상대적 측정 위치를 나타내며, 각 나타낸 속도는 최고 속도로 무차원화 하였다. 축 방향 및 원주방향 속도는 러너 간극이 적용됨에 따라 속도 분포의 차이를 나타냈으며, 특히 러너 콘을 통한 누설 유동이 발생하는 중앙 부분(d/D=0.5)에서 가장 큰 차이를 나타냈다. 한편, 축 방향 속도는 흡출관의 유동진행 방향을 따라 p3에서 속도 차이가 점차 감소하는 특성을 나타냈다. 따라서 러너 및 콘 간극을 통한 누설 유동은 러너 및 흡출관 내 유동에 영향을 주지만, 그 차이는 미비하며, 이로 인해 약간의 head 및 성능 손실에 영향을 주는 것으로 볼 수 있다.
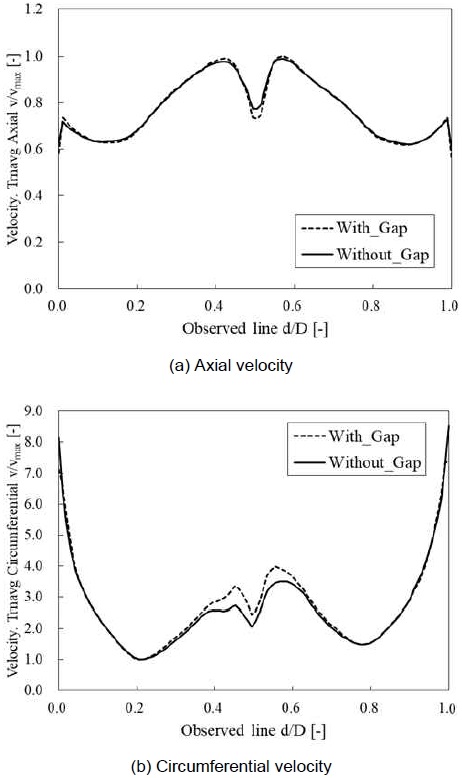
Time-averaged axial and circumferential velocities on the observed line of 0.1 D2 in the draft tube at QED=0.30 (best efficiency point)

Time-averaged axial and circumferential velocities on the observed line of 0.3D2 in the draft tube at QED=0.30 (best efficiency point)
Figs. 10, 11은 프란시스 수차 모델의 BEP 조건에서 Fig. 2에 도시된 GV 출구 및 흡출관 벽면의 압력 측정점에서의 러너 간극에 따른 비정상 압력값으로부터 고속 퓨리에 변환(fast fourier transform, FFT) 분석을 통해 날개 통과 주파수(blade passing frequency) 등 비정상 압력 특성을 검토하였다. 여기서 magnitude는 GV 출구 및 흡출관의 각 최대값으로 무차원화 하였고, 주파수는 프란시스 수차 모델의 날 개통과주파수(fn)로 무차원화 하였다. Fig. 10에서 GV 출구의 압력 특성은 3개의 압력 측정점 모두 1차 날개통과주파수 등 유사한 비정상 압력 특성을 나타냈으며, 러너 간극을 적용한 압력 분포에서도 크게 차이를 나타내지 않았다. Fig. 11은 흡출관 내 비정상 압력 특성으로, p1부터 p9까지 유동 진행 방향에 따라 압력값이 점차 감소하는 특성을 나타냈으며, 저주파수 영역에서는 간극에 따라 약간 다른 특성을 나타내지만, 동일한 측정점에서 1차 날개 통과 주파수 등 비정상 압력 특성이 전반적으로 유사하게 발생하는 것을 볼 수 있다. 따라서 러너 및 콘 간극을 통한 누설 유동으로 인해 프란시스 수차 모델의 비정상 압력 특성에 영향을 주지만, 러너 간극의 적용으로 인해 두드러지는 차이는 나타나지 않았다.
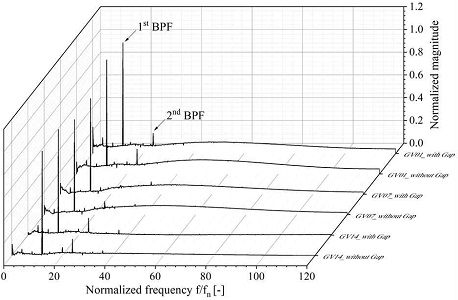
Normalized unsteady pressure distributions at the outlet of guide vanes (GV01, 07, 14) with and without gap
4. 결 론
본 연구에서는 프란시스 수차 모델의 러너 및 콘 간극의 누설 유동에 대한 내부 유동 및 성능 특성을 검토하기 위해 삼차원 비정상 상태 RANS 해석을 수행하였다. 최고효율점 및 인근 유량 조건에 대해 head 손실을 검토하여 성능 감소의 범위를 확인하였으며, 압력 및 유선 분포를 통해 러너 간극의 내부 유동 특성을 검토하였다. 특히, 최고효율점에서 간극 유무에 따른 러너 및 흡출관 내 속도 분포의 비교를 통해 러너 간극의 누설 유동에 의해 유발되는 유동 특성의 차이를 확인하였다. 또한, GV 출구 및 흡출관 벽면의 비정상 압력값으로부터 FFT 분석을 통해 간극에 따른 비정상 압력 특성을 확인하였다. 이와 같은 결과를 토대로, 본 연구에 적용된 허브 및 슈라우드에서 최소 간격을 각각 약 0.000403D2 및 0.000461D2로 가지는 러너 간극의 경우, 러너 간극에 의한 누설 유동으로 인해 내부 유동 및 성능에 차이는 발생하지만 그 차이가 매우 미비하고, 두드러지는 유동 특성의 차이가 발생하지 않았다. 그러므로 삼차원 정밀 수치해석의 시간 및 비용을 고려하여 볼 때 수치해석의 대상이 되는 프란시스 수차 모델의 러너 간극 크기에 따라 전체 유동 도메인 단순화 범위를 고려하여 효율적인 수치해석의 수행을 기대할 수 있다.
Acknowledgments
본 연구는 국토교통부/국토교통과학기술진흥원의 지원으로 수행되었습니다(과제번호 20IFIP-B128593-04).
References
-
W. Zhao, T. K. Nielsen, and J. T. Billdal, “Effects of cavity on leakage loss in straight-through labyrinth seals”, IOP Conference Series: Earth and Environmental Science, Vol. 12, No. 1, 2010, p. 012002. Retrieved from https://iopscience.iop.org/article/10.1088/1755-1315/12/1/012002/meta, .
[https://doi.org/10.1088/1755-1315/12/1/012002]

-
D. Čelič and H. Ondráčka, “The influence of disc friction losses and labyrinth losses on efficiency of high head Francis turbine”, Journal of Physics: Conference Series, Vol. 579, No. 1, 2015, p. 012007. Retrieved from https://iopscience.iop.org/article/10.1088/1742-6596/579/1/012007/meta, .
[https://doi.org/10.1088/1742-6596/579/1/012007]

-
J. Feng, X. Luo, G. Zhu, and G. Wu, “Investigation on disk friction loss and leakage effect on performance in a Francis model turbine”, Advances in Mechanical Engineering, Vol. 9, No. 8, 2017, pp. 1-10.
[https://doi.org/10.1177/1687814017723792]

-
S. J. Kim, Y. S. Choi, Y. Cho, J. W. Choi, J. J. Hyun, W. G. Joo, and J. H. Kim, “Analysis of the numerical grids of a Francis turbine model through grid convergence index method”, The KSFM Journal of Fluid Machinery, Vol. 23, No. 2, 2020, pp. 16-22.
[https://doi.org/10.5293/kfma.2020.23.2.016]

- IEC 60193 Ed. 2.0, “Hydraulic turbines, storage pumps and pump-turbines model acceptance tests”, American National Standards Institute, 1999. Retrieved from https://infostore.saiglobal.com/preview/98687781138.pdf?sku=872218_SAIG_NSAI_NSAI_2073849, .
- ANSYS CFX-19.1, “ANSYS CFX-solver theory guide”, ANSYS Inc., 2018.
-
L. F. Richardson, “The approximate arithmetical solution by finite differences of physical problems involving differential equations, with an application to the stresses in a masonry dam”, Philosophical Transactions of the Royal Society of London. Series A, Vol. 210, 1991, pp. 307-357.
[https://doi.org/10.1098/rsta.1911.0009]

-
L. F. Richardson and J. A. Gaunt, “The deferred approach to the limit”, Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character, Vol. 226, 1927, pp. 299-361.
[https://doi.org/10.1098/rsta.1927.0008]

-
I. B. Celik, U. Ghia, P. J. Roache, C. J. Freitas, H. Coleman, and P. E. Raad, “Procedure for estimation and reporting of uncertainty due to discretization in CFD applications”, ASME J. Fluids Eng., Vol. 130, 2008, pp. 078001.
[https://doi.org/10.1115/1.2960953]

- Korea Agency for Infrastructure Technology Adcancement, “Report development of construction technology for medium sized hydropower plant”, Korea Agency for Infrastructure Technology Advancement, Report No. 17IFIP-B128593-01, 2017. Retrieved from https://www.open.go.kr/, .