[ Article ]

Transactions of the Korean Hydrogen and New Energy Society - Vol. 31, No. 3, pp.314-321

ISSN: 1738-7264 (Print) 2288-7407 (Online)

Print publication date 30 Jun 2020

Received 27 Apr 2020 Revised 23 May 2020 Accepted 30 Jun 2020

DOI: https://doi.org/10.7316/KHNES.2020.31.3.314

2.5 kW 급 프로펠러형 마이크로 수차 개발

마상범¹ ; 김성¹ ; 최영석¹^{, 2} ; 차동안¹ ; 김진혁¹^{, 2}^{, †}

1한국생산기술연구원 청정에너지시스템연구부문
2과학기술연합대학원 대학교 생산기술전공

Development of 2.5 kW Class Propeller Type Micro Hydraulic Turbine

SANG-BUM MA¹ ; SUNG KIM¹ ; YOUNG-SEOK CHOI¹^{, 2} ; DONG-AN CHA¹ ; JIN-HYUK KIM¹^{, 2}^{, †}

1Clean Energy R&D Department, Korea Institute of Industrial Technology, 89 Yangdaegiro-gil, Ipjang-myeon, Seobuk-gu, Cheonan 31056, Korea
2Industrial Technology, University of Science and Technology, 217 Gajeong-ro, Yuseong-gu, Daejeon 34113, Korea

Correspondence to: ^† jinhyuk@kitech.re.kr

Abstract

In this work, a preliminary design of an inlet guide vane and runner for developing a 2.5 kW hydraulic turbine was conducted by using computational fluid dynamic analysis. Three-dimensional Reynolds-averaged Navier-Stokes equations with shear stress transport turbulence model were used to analyze the fluid flow in the hydraulic turbine. The hexahedral grid system was used to construct computational domain, and the grid dependency test was performed to obtain the optimal grid system. Velocity triangle diagram considering the flow angles of the inlet guide vane and runner was analyzed to obtain a basic geometry of the inlet guide vane and runner. Through modification of the preliminary design, the hydraulic performances of the turbine have improved under overall drop conditions. Especially, the efficiency and power of the turbine increased by 0.95% and 1.45%, respectively, compared to those of the reference model.

Keywords:

Hydraulic turbine, Computational fluid dynamics, Inlet guide vane, Runner

키워드:

수차, 전산유체역학, 입구 가이드 베인, 러너

1. 서 론

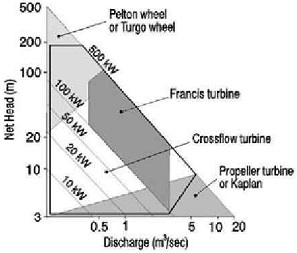
수력 발전은 공해가 없는 에너지를 생성할 수 있으며, 다른 대체에너지와 비교하여 상대적으로 높은 에너지 밀도를 가지고 있다. 소수력 발전은 일반하천, 저수지, 하수처리장 등 기존 구조물을 이용하여 개발이 가능하며, 저낙차 조건에서도 설치하여 운용할 수 있다. 특히, 최근에는 저낙차 조건에서 설치하는 수차를 마이크로(micro) 수차로 분류하여 소규모 수원지 및 관로 등에 적용한 연구가 주목을 받고 있다¹⁾.

Fig. 1과 같이 마이크로 수차는 저낙차 운용 조건에 따라 프로펠러(propeller) 형태의 수차가 적합하며²⁾, 러너(runner)와 가이드 베인(guide vane)에 의해 수력학적 성능이 좌우된다^3-5). Li 등⁴⁾은 수차의 운용 조건에 따른 수력학적 성능을 수치해석을 통해 분석하였고, 가이드 베인의 개도 각도에 따른 영향성을 연구하였다. Park 등⁵⁾은 러너의 깃 수 변화에 따른 수차의 성능을 유동해석을 통해 분석하였으며, 저유량에서 깃 수가 증가할수록 높은 효율을 얻을 수 있다고 보고하였다. 본 연구에서는 2.5 kW 급 범용 마이크로 수차를 개발하기 위해 기초 설계된 러너를 사용하였다. 유동해석을 통해 러너의 수력학적 성능 분석을 수행하였고, 2.5 kW에서 최고효율점이 형성되도록 입구 가이드 베인(inlet guide vane, IGV)을 설계하였다.

Fig. 1.

Classification of the hydraulic turbines2)

ANSYS사(Pennsylvania Cannonsburg, USA)의 Blade-gen을 사용하여 러너와 IGV를 5개의 스팬으로 나누어 형상을 제어하였고, 3차원 Reynolds-averaged Navier-Stokes (RANS) 방정식 해석을 수행하였다.

2. 수치해석 방법

본 연구에서는 프로펠러 수차의 성능을 예측하기 위한 삼차원 비압축성 RANS 해석을 ANSYS CFX 15.0⁶⁾을 통해 수행하였고, 난류모델로는 shear stress transport (SST) 난류 모델⁷⁾을 사용하였다.

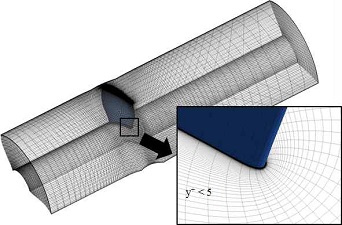
본 연구에서 사용된 러너는 3매로 구성되었으며, 3.0 m의 낙차 조건에서 최고효율점(best efficiency point, BEP)이 형성된다. 자세한 설계사양은 Table 1에 나타내었다. 계산 시간의 단축과 수렴성 향상을 위해 계산영역은 Fig. 2와 같이 주기조건을 부여하여 단일 유로 형태로 구성하였다.

Table 1.

Design specifications of the reference runner

Fig. 2.

Computational domain of the reference runner model

작동유체는 25˚C의 물을 사용하였으며, 입구 경계조건으로 낙차에 따른 전압력 조건을 부여하였고, 출구 경계조건은 표준 상태의 대기압으로 가정하였다. 러너의 표면에는 O형 격자를 사용하여 격자계를 구성하였고, Low-Reynolds number SST 모델 사용을 위해 y⁺가 5 미만으로 유지되도록 하였다.

격자의존성을 제거하기 위해 Richardson 외삽법을 기반으로 한 이산화 오류 예측법^8,9)을 사용하여 최적의 격자계를 선정하였다. 이를 위해 3개의 서로 다른 격자계(N₁, N₂ 및 N₃)를 구성하였고, 격자 세분화 인자(grid refinement factor, r)를 1.3으로 설정한 격자 의존성 시험 결과를 Table 2에 나타내었다. 이를 위해 다음과 같이 정의된 러너의 수력학적 효율을 사용하였다.

η = τ ω ∆ P t Q × 100 %

(1)

Table 2.

Grid dependency test using grid convergence index

여기서 τ와 ω는 각각 러너에 작용하는 토크와 회전 속도를 의미하며, ∆P_t와 Q는 각각 입출구 전압력차와 유량을 의미한다.

Table 2에 나타낸 바와 같이 격자수가 증가할수록 러너의 수력학적 효율이 점차 수렴하는 경향을 보이며, N₁을 사용한 경우 외삽 상대 오차(e_ext²¹)와 격자 수렴 지표(grid convergence index, GCI)는 각각 9.68E-06% 및 1.21E-03%로 예측되어 매우 적은 수치적 불확실성이 확인되었다. 이 결과를 바탕으로 N₁을 최적의 격자계로 선정하였고, Fig. 3에 나타내었다.

Fig. 3.

Optimal grid system of the runner

3. 러너 성능 분석 및 IGV 설계

Fig. 4는 본 연구에서 사용한 러너의 성능곡선을 나타내었다. 낙차 조건을 1.0 m에서 5.0 m까지 변화시키면서 러너의 출력(P), 수두(Head) 및 효율을 예측하였고, 각 성능함수의 정의는 다음과 같다.

P = τ × ω

(2)

H e a d = ∆ P t ρ g

(3)

Fig. 4.

Performance maps of the reference runner

여기서 ρ와 g는 각각 작동유체의 밀도와 중력가속도를 의미한다.

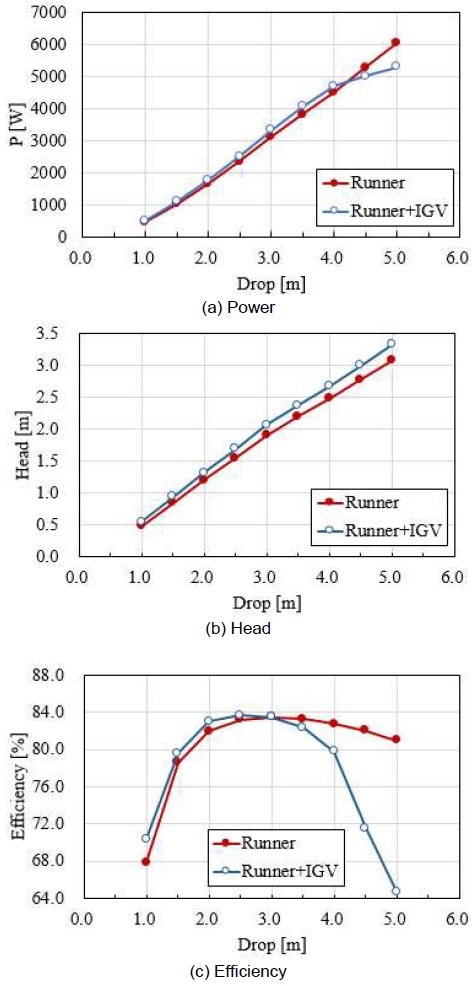
러너의 유효 수두와 출력은 낙차가 커질수록 증가하는 경향을 보이고 있으며, 효율은 Fig. 4(c)에 나타낸 바와 같이 3.0 m의 낙차에서 BEP가 83.33%로 형성되었다. 이때 출력은 약 3.0 kW로 예측되었다(Fig. 4[a]).

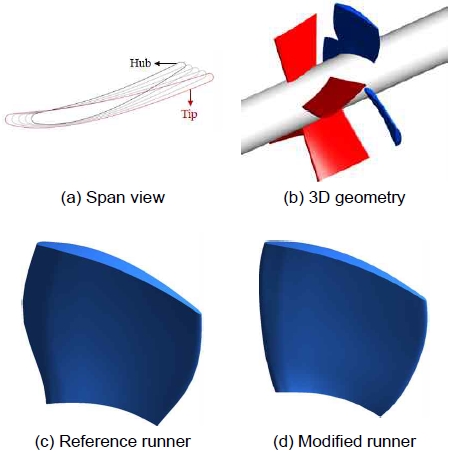
서론에서 언급한 바와 같이 본 연구에서는 2.5 kW급 범용 마이크로 수차 개발을 목적으로 하기 때문에 IGV를 설계하여 연구 목적을 달성하고자 하였다. Fig. 4(a)에서 알 수 있듯이 본 연구에 사용된 러너의 경우 2.5 m 낙차에서 출력이 2.5 kW로 예측된다. 따라서 IGV를 활용하여 BEP가 형성되는 낙차를 2.5 m로 제어하고자 하였다. IGV는 ANSYS사의 Blade-gen을 사용하여 설계하였으며, Table 3에 나타낸 바와 같이 허브(hub)부터 팁(tip)까지 5개의 스팬(span)으로 구성하여 IGV의 출구 각도를 제어하였다. 회전방향 속도 성분을 고려하여 허브 부근에서는 상대적으로 pre-swirl을 크게 생성할 수 있도록 출구 각도를 35˚로 설정하였고, 팁 부분으로 갈수록 출구 각도를 감소시켰다. IGV는 4매로 구성하였고, 삼차원 형상 및 스팬별 형상 정보는 Fig. 5에 나타내었다. IGV를 포함한 유동해석에 앞서 IGV에 대한 격자 의존성 시험을 러너와 동일하게 GCI 방법을 적용하여 수행하였고, 약 57만 개의 격자수를 사용하였을 때 격자 의존성이 제거되는 것을 확인하였다. 아울러, 회전 도메인과 정지 도메인 사이의 경계조건으로는 frozen-rotor 방법을 적용하였다. 기초 설계된 IGV와 러너의 수력학적 성능을 계산하여 Fig. 6에 나타내었다.

Table 3.

Blade angle distributions

Fig. 5.

Preliminary inlet guide vane model and modified runner

Fig. 6.

Performance maps of the reference runner with inlet guide vane

IGV로 인해 전체 낙차 조건에서 러너의 수두가 증가한 것을 확인할 수 있으며(Fig. 6[b]), BEP가 2.5 m 낙차 조건일 때 형성되었고, 이때의 출력이 약 2.5 kW로 예측된 것을 확인하였다(Fig. 6[a]). 그러나 고낙차 조건일 때(drop >4.0 m), 수차의 출력과 효율이 급격하게 저하되었다.

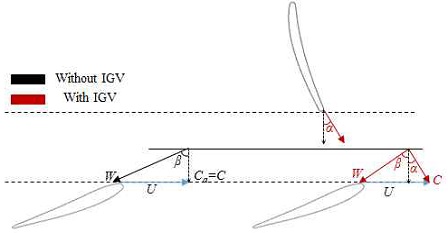
이러한 현상은 IGV로 인해 발생한 pre-swirl이 러너의 입구 각도와 mismatching 되어 발생한 것으로 판단하여 고낙차 조건일 때(4.5 m) 러너 전연(leading edge)에서의 유동 각도를 분석하여 Table 4와 Fig. 7에 나타내었다. 고낙차 조건에서는 설계 조건과 비교하여 상대적으로 유량이 증가하기 때문에 축방향 속 도(C_a)가 증가하게 되어 상대 유동각도(β)가 감소한다. 기초설계된 IGV를 사용하게 되면 pre-swirl을 형성하여 절대 유동각도(α)를 증가시키게 되므로 상대유동각도가 더욱 감소하게 되어 러너의 전연부 입구 각도와 차이가 증가하게 된다. 본 연구에서 사용한 IGV는 허브 부분에서 출구 각도가 상대적으로 크기 때문에 Table 4에 나타낸 바와 같이 허브부터 50% 스팬까지 유동의 영각(Incidence angle)이 상대적으로 큰 것을 알 수 있다.

Table 4.

Inlet blade angle and flow angle distributions of the reference runner at 4.5 m drop condition

Fig. 7.

Velocity triangle diagrams with and without inlet guide vane

이러한 문제를 해결하기 위해 러너의 입구 각도를 Table 5와 같이 변경하였고, 이를 적용한 수차의 수력학적 성능을 계산하여 Fig. 8에 나타내었다. 수정된 러너를 사용한 경우 수차의 수력학적 성능이 전체 낙차 조건에서 향상된 것을 확인하였고, 2.5 m 낙차조건에서 BEP를 형성하고 이때의 출력이 2.5 kW로 예측되었다. 아울러 BEP에서 효율은 기존의 러너를 사용한 수차와 비교하여 약 1% 향상되었다.

Table 5.

Adjustment of the runner’s inlet angle

Fig. 8.

Performance maps of the modified runner with inlet guide vane

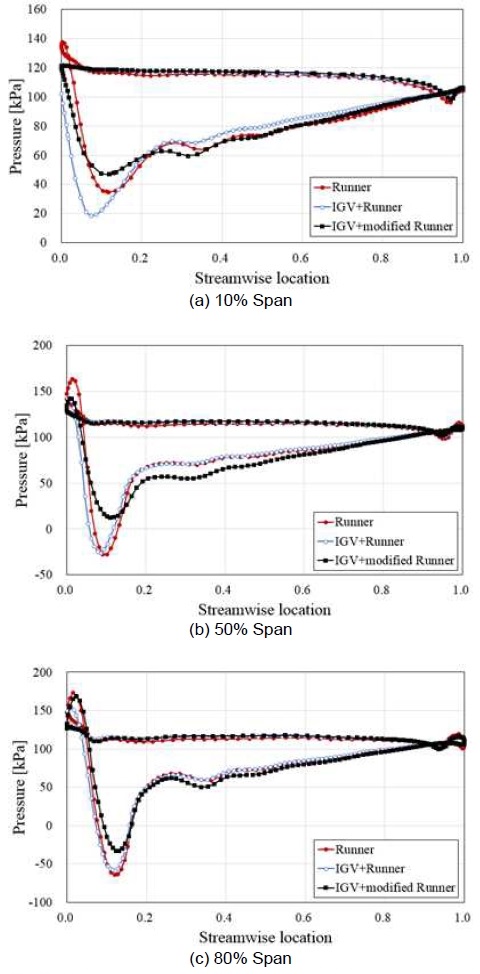
Fig. 9는 BEP에서 러너의 스팬별 압력 분포를 나타내었다. 기존 러너를 사용한 경우 IGV의 유무에 상관없이 50% 및 80% 스팬에서 압력 분포에 영향이 없었지만, 10% 스팬에서는 IGV를 사용하였을 때 유동방향으로 전연부터 20% 코드(chord)까지 흡입면에서 압력이 크게 감소하여 압력면과 흡입면의 압력차가 상대적으로 큰 것을 알 수 있다. 반면, 수정된 러너를 사용하면 전체 스팬에서 전연부터 20% 코드까지 흡입면에서 압력이 증가하지만 20% 코드부터 후연(trailing edge)까지 흡입면과 압력면에서의 압력차가 증가한 것을 확인할 수 있다. 이로 인해 러너의 토크(torque)가 증가한 것으로 사료되며, 결과적으로 수차의 출력이 증가한 효과를 얻을 수 있었다.

Fig. 9.

Pressure distributions of the runner at best efficiency point

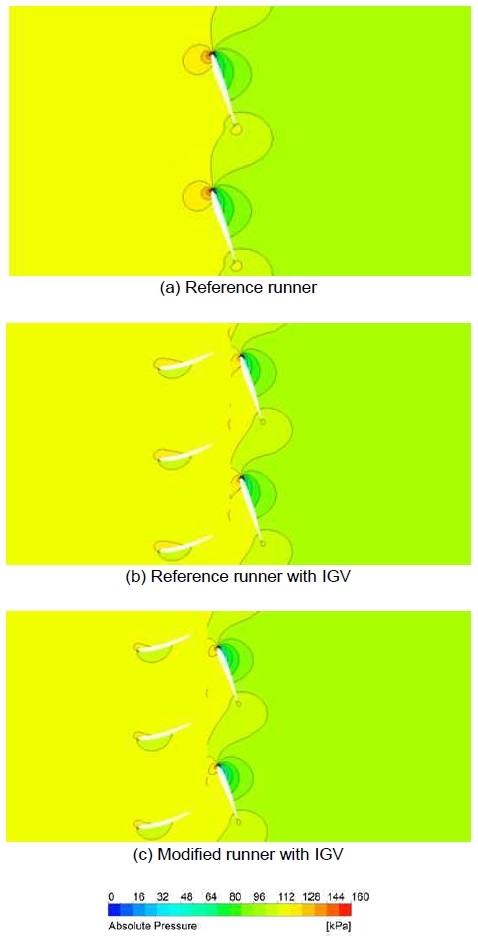
한편 Fig. 9(b), (c)에서 나타난 바와 같이 러너의 전연에서 흡입면과 압력면에서 압력이 역전되는 현상이 관찰되었다. 이를 분석하기 위해 Fig. 10에 50%스팬에서 압력분포를 비교하였다. Fig. 10(a)에서 보는 바와 같이 러너의 흡입면에서 정체점(stagnation point)이 발생하여 정압이 급격하게 증가한 것을 확인할 수 있다. 반면 IGV를 사용한 경우, 러너 전연부에서 유동 각도가 제어되어 Fig. 10(b), (c)에 나타난 바와 같이 정체점이 러너의 전연부 근처로 이동하게 되고, 압력이 역전되는 현상이 완화되는 것을 알 수 있다(Fig. 9[b], [c]). 즉, IGV가 정체점의 위치에 영향을 미치고, 러너 표면에 작용하는 압력 분포에 밀접한 연관이 있다는 것을 관찰하였다.

Fig. 10.

Pressure distributions of the runner’s 50% span at best efficiency point. IGV, inlet guide vane.

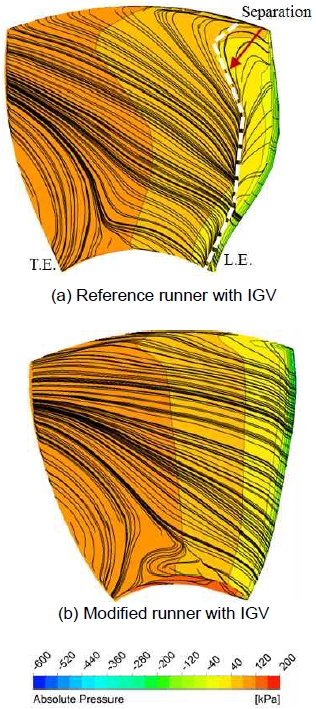
Fig. 11은 4.5 m의 고낙차 조건에서 러너 흡입면의 압력 및 유선 분포를 나타내고 있다. 기존 러너를 사용한 경우 Fig. 11(a)와 같이 흡입면의 전연부 근처에서부터 유동 박리가 발생하는 것을 알 수 있다. 또한 러너 흡입면의 압력 분포는 유동 박리 경계를 따라 형성되는 것을 관찰할 수 있다. 이와 반대로 수정된 러너는 입구 각도와 유동 각도의 차이가 감소하여 유동이 러너의 표면을 따라서 매끄럽게 진행되는 것이 관찰되었고, 압력 분포가 스팬 방향으로 고르게 분포하는 것을 확인하였다(Fig. 11[b]).

Fig. 11.

Pressure and streamline distributions of the runner at 4.5 m drop condition. IGV, inlet guide vane.

또한, 기존 러너의 경우 흡입면에서 유동 박리 경계를 따라 상대적으로 넓은 영역에서 고압이 형성되는 것을 알 수 있고, 그로 인해 압력면과의 압력차가 감소하여 출력이 저하되는 것으로 사료된다.

4. 결 론

본 연구에서는 기존 러너를 활용한 2.5 kW 급 범용 수차 설계를 위해 유동해석을 수행하였다. BEP에서 설계 출력을 도출하기 위해 IGV의 기초 설계 및 러너 입구 각도 조정을 진행하였다. 본 연구를 통해 기초 설계된 IGV와 수정된 러너를 사용한 수차는 기존 러너를 사용한 수차와 비교하여 BEP에서 수차의 효율과 출력이 각각 0.95% 및 1.45% 향상되었고, 고낙차 조건(4.5 m)에서 효율과 출력이 각각 10.46% 및 14.95% 향상되었다.

본 연구를 통해 도출된 IGV와 러너는 속도 삼각형 분석을 바탕으로 한 기초설계 수준임을 고려하여 향후 연구에서는 수차의 수력학적 성능을 극대화하기 위해 최적설계가 필요하다고 사료되며, 실험을 통한 성능 검증을 위하여 형상 제작 및 실험 설비를 구축하고 있다.

Acknowledgments

본 연구는 과학기술정보통신부의 재원으로 한국생산기술연구원의 생산기술 산업선도 핵심기술 개발사업(No. EO200019)의 일환으로 수행되었음을 밝히며 이에 감사드립니다.

References

N. H. Park and Y. W. Rhee, “Output optimization of microhydro kaplan turbine by double regulating runner and guide vane”, The KSFM Journal of Fluid Machinery, Vol. 16, No. 1, 2013, pp. 17-23. [https://doi.org/10.5293/kfma.2013.16.1.017]
M. T. Gatte and R. A. Kadhim, “Hydro power”, Open access peer-reviewed chapter.
D. Y. Kim and Y. T. Kim, “Design and performance analysis of a 115 kW class bulb-type hydro-turbine”, Journal of the Korean Society of Marine Engineering, Vol. 42, No. 4, 2018, pp. 304-311. [https://doi.org/10.5916/jkosme.2018.42.4.304]
K. M. Li, W. Kwon, and Y. W. Lee, “Numerical study on effects of guide vane opening of a bulb turbine”, Journal of the Korean Society of Marine Engineering, Vol. 43, No. 7, 2019, pp. 528-534. [https://doi.org/10.5916/jkosme.2019.43.7.528]
J. H. Park, Y. T. Kim, Y. Cho, B. K. Kim, and Y. H. Lee, “Performance analysis of 10kW class propeller hydro turbine by the change of flow rates and the number of runner vane using CFD”, The KSFM Journal of Fluid Machinery, Vol. 17, No. 2, 2014, pp. 5-11. [https://doi.org/10.5293/kfma.2014.17.2.005]
“ANSYS CFX-15.0, ANSYS CFX-solver theory guide”, ANSYS Inc., 2013. Retrieved from https://read.pudn.com/downloads500/ebook/2077964/cfx_thry.pdf, .
F. R. Menter, “Review of the shear-stress transport turbulence model experience from an industrial perspective”, International Journal of Computational Fluid Dynamics, Vol. 23, No. 4, 2009, pp. 305-316. [https://doi.org/10.1080/10618560902773387]
P. J. Roache, “Verification of codes and calculations”, AIAA Journal, Vol. 36, No. 5, 1998, pp. 696-702. [https://doi.org/10.2514/2.457]
I. Celik and O. Karatekin, “Numerical experiments on application of richardson extrapolation with nonuniform grids”, J. Fluids Eng., Vol. 119, No. 3, 1997, pp. 584-590. [https://doi.org/10.1115/1.2819284]