[ Article ]

Transactions of the Korean Hydrogen and New Energy Society - Vol. 31, No. 6, pp.558-563

ISSN: 1738-7264 (Print) 2288-7407 (Online)

Print publication date 31 Dec 2020

Received 21 Oct 2020 Revised 01 Dec 2020 Accepted 30 Dec 2020

DOI: https://doi.org/10.7316/KHNES.2020.31.6.558

Type Ⅲ 수소 저장 용기에서 가스 모델(gas model)에 따른 배출(discharge) 현상의 수치 해석적 연구

김무선¹ ; 류준형² ; 정수연³ ; 이성우³ ; 최성웅³^{, †}

1한국철도기술연구원 도시철도연구팀
2한국철도기술연구원 추진시스템연구팀
3경상대학교 기계시스템공학과

Numerical Analysis of Discharge Flow in Type Ⅲ Hydrogen Tank with Different Gas Models

MOO-SUN KIM¹ ; JOON-HYOUNG RYU² ; SU YEON JUNG³ ; SEONG WOO LEE³ ; SUNG WOONG CHOI³^{, †}

1Urban Transit Research Team, Korea Railroad Research Institute, 176 Cheoldobangmulgwan-ro, Uiwang 16105, Korea
2Propulsion System Research Team, Korea Railroad Research Institute, 176 Cheoldobangmulgwan-ro, Uiwang 16105, Korea
3Department of Mechanical System Engineering, Gyeongsang National University, 2-13 Tongyeonghaean-ro, Tongyeong 53064, Korea

Correspondence to: ^† younhulje@gnu.ac.kr

Abstract

Hydrogen is attracting attention as an alternative energy source as an eco-friendly fuel without emitting environmental pollutants. In order to use hydrogen as an energy source, technologies such as hydrogen production and storage must be used, and new storage methods are being studied. In this study, the behavior of hydrogen in the storage tank were numerically studied under high-pressure hydrogen discharge conditions in a Type III hydrogen tank. Numerical results were compared with the experimental value and the results were quantitatively analyzed to verify the numerical implementation. With the results of pressure and temperature values under a given discharge condition, the Redich-Kwong gas model showed the adequate models with the smallest error between numerical and experimental results.

Keywords:

Hydrogen tank, Type III, Numerical analysis, Gas model

키워드:

수소저장탱크, 타입3, 수치해석, 가스모델

1. 서 론

수소는 무게 대비 에너지 밀도가 높을 뿐 아니라 환경오염물질 배출이 없는 친환경 연료이자 최종 부산물의 재사용이 가능하여 대체에너지원으로 크게 각광을 받고 있다. 수소를 에너지원으로 활용하기 위해서는 수소의 생산, 저장과 같은 기술을 활용해야 하며 저장 및 운송에 대한 기술은 새로운 방법들이 제안되고 연구되어 왔다. 하지만 각기 다른 장단점으로 인해 활용도가 달라지고 있다. 수소 저장 기술방법에는 압축 기체 저장법, 액체수소 저장법 및 수소저장소재를 이용한 저장법 등이 있다¹⁾. 압축 기체 저장법과 액체수소 저장법은 현재 일반적으로 적용되는 방법이지만, 압축 기체 저장법의 경우 상대적으로 체적 당 저장밀도가 낮고 고압의 가스용기를 사용함으로써 위험성이 크다는 단점이 존재한다. 액체수소 저장법은 체적 당 저장밀도가 압축 기체 저장법보다 크지만 수소의 액화점의 -235℃ 이하로 유지되어야 하는 특수 단열 시스템이 요구되고 장시간의 저장에 기술적 한계가 존재한다(Table 1). 따라서 현재의 기술과 활용성 면에서 고압기체 저장법이 주로 사용되고 있으며 이를 통해 저장 운송 시스템에 적용방법이 모색되고 있다. 통상적으로 운송용으로 사용되는 가압 기체 수소저장시스템은 수소기체를 고압으로 압축하여 제한된 체적의 용기에 저장하는 방식으로 약 70 MPa 정도의 고압 수소기체를 저장하고 공급한다. 수소저장시스템은 탱크 주위의 화재와 같은 탱크의 손상이 야기되는 상황이나 정기적인 유지 보수를 수행해야 하는 상황 시 내부의 압축 수소를 외부로 안전하게 배출하는 기능을 충족해야 한다. 내부의 고압 압축 수소를 외부 대기압에 배출 시, 갑작스런 고압가스 배출로 용기 내부 온도가 급강하하는 현상이 발생할 수 있고 급강하된 온도 환경으로 인해, 고분자로 성형된 라이너 및 그 주변을 와인딩하고 있는 탄소섬유 메트릭스(matrix)는 극저온 온도에 노출된다. 이런 환경에서는 고압 기체수소로 팽창되어 있던 용기가 빠른 속도로 수축 변형이 일어날 가능성이 발생한다. 따라서 배출 조건에서도 안정적인 저장 시스템의 운용을 위해 저장 용기의 특성변화를 예측할 수 있는 수치해석 기반의 검토가 필요하다. 가스의 배출에 대한 연구는 가스터빈²⁾에서부터 자동차 배출가스³⁾, 메탄가스 배출에 대한 연구⁴⁾ 등 다방면으로 진행되었으며 배출 조절 및 제어를 위한 연구⁵⁾들이 수행되었다.

Table 1.

Advantages and disadvantages of hydrogen storage methods9)

수소 저장 탱크에서 내부의 고압 압축 수소의 거동에 관한 연구는 수소 밀도의 변화에 대한 연구⁶⁾에서부터 수소 충전에 대한 연구^7,8) 들까지 다방면으로 진행되었다. 수소 배출 조건에서 수소의 거동에 따른 저장 탱크의 변화에 관한 연구는 일부가 수행되었으나 수요나 필요성에 의한 응용 연구가 더 필요한 실정이다.

본 연구에서는 Type Ⅲ 수소 저장 탱크를 대상으로 고압 수소의 배출 조건에서 수소의 거동과 저장 탱크의 변화를 수치적으로 모사하였다. 특히 수소 유체의 정확한 모사를 위해 수소의 가스 모델(gas model)에 따른 정확성과 유체 거동의 영향성에 대해 논의하고 적합한 gas model을 선정하였다.

2. 배경

2.1 수소 저장 용기의 특징

고압 기체 저장은 현재 일반적으로 사용하는 방식으로 수소기체를 15-70 MPa 등의 고압으로 압축하여 고압 용기에 저장하는 방식이다. 무게 밀도가 13%, 부피 밀도가 40 kg/m³로 낮은 단점이 있고 공간상의 제약이 많아 높은 수송비의 제약이 있으나 충전 방법이 간단하여 많이 사용되고 있다⁹⁾.

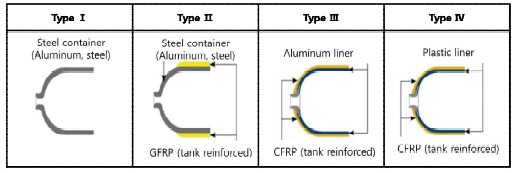
수소의 낮은 부피 밀도로 인해 고압으로 압축 시 많은 양의 수소를 저장할 수 있는 이점으로 수소를 기체형태로 저장하는 것이다. 압축 방식으로 수소를 저장하기 위해서는 용기가 필요한데 압축 용기는 용기의 몸통부분과 내측(라이너) 부분을 제작하는 재질 및 구성, 강도에 따라 Fig. 1에서 보는 바와 같이 복합 용기를 Type 1-4와 같이 구분할 수 있다. 이 중 Type 3 복합 용기와 Type 4 복합 용기가 수소자동차 미래시장에 적합성을 두고 기술경쟁을 펼치고 있다. 이 두 가지 유형의 복합 용기 중 Type 3은 용기 전체를 유리섬유 또는 탄소섬유 등으로 적층시킨 구조의 용기인데 용기 내부 하중의 대부분을 복합재료 부분에서 감당하므로 내부 금속 라이너 부분에서는 가해지는 하중이 비교적 작아지는 특징이 있다. Type 4는 고밀도 폴리에틸렌(high-density polyethylene, HDPE)과 같은 비금속 라이너에 에폭시 계열의 함침 수지를 연속 섬유(탄소섬유)를 용기에 감은 후 가열한 용기이다.

Fig. 1.

Characteristics of hydrogen storage tanks

3. 수치 해석

수소 배출에 대한 모델링을 수립하고 정식화하는 과정에서는 수치 해석의 해석 기법을 검증하는 과정이 필요하다. 따라서 존재하는 실험값과 비교 검증을 통해 검증과정이 진행되었다. 비교 검증은 Type 3 형태의 고압 탱크의 실험값을 토대로 진행되었고 Type 3 탱크를 모델로 선정하였다. 해석을 위한 고압 탱크는 74 L 용량의 실린더로 내부 길이가 849 mm, 내경이 354 mm로 되어 있으며 normal working pressure 70 MPa인 고압 탱크이다. 고압의 수소 배출을 통한 내부 상태 변화를 위한 수치 해석적 접근법은 고압 기체의 배출에 따른 탱크 내부의 압력 변화와 열전달을 동시에 해결하는 문제로 정식화할 수 있다.

3.1 모델링

Type 3 모델을 통한 수소 배출 해석에서는 상용 해석 프로그램인 ANSYS(Canonsburg, PA, USA)의 design modeler를 이용하여 Type 3의 고압 탱크 형상과 해석영역의 구성을 geometry로 생성하였으며 형상에 대한 크기 정보와 물성치는 Table 2에 나타내었다.

Table 2.

Dimensions of the tank and its material properties

수소 가스 거동에서 gas model을 선택하는 것이 중요하다. 본 연구에서는 다양한 gas model들을 대상으로 배출(discharge) 현상에 적합한 gas model의 선정에 중점을 두었다. 이를 위해 4가지 gas model을 대상으로 gas flow behavior를 살펴보았다. 4가지 gas model은 Redlich-Kwong equation¹⁰⁾, Soave’s modified Redlich-Kwong equation¹¹⁾, Aungier’s modified Redlich-Kwong equation¹²⁾과 Peng-Robinson equation¹³⁾이다.

3.2 지배방정식

수소 저장 탱크 내부유동은 2차원 비정상 상태, 압축성 난류 유동으로 설정하였고, 작동 유체의 밀도는 real gas effects를 지배방정식에 적용하여 산출하였다. 연속방정식과 momentum conservation 방정식, 에너지 방정식은 다음과 같다.

∂ ρ ∂ t + ∂ ∂ x i ρ u i = 0 ∂ ρ ∂ t ρ u i + ∂ ∂ x j ρ u i u j = - ∂ p ∂ x i + ∂ ∂ x j μ ∂ u i ∂ x j + ∂ u j ∂ x i - 23 δ i j ∂ u l ∂ x l + ∂ - ρ u i' u j' ¯ ∂ x j ∂ ∂ t ρ C p T + ∂ ∂ x j ρ u j C p T = ∂ ∂ x j k ∂ T ∂ x j

(ρ: density, t: time, u: velocity tensor, x: distance, subscript i: direction (i=1, 2, 3은 각각 x, y, z 방향), p: pressure, C_ρ: specific heat, T: temperature, k: thermal conductivity)

본 해석 연구에 적합한 난류 모델을 설정하기 위해 two equation 모델 중 k-ε model을 선정하였으며, 그 지배방정식은 다음과 같다.

∂ ∂ t ρ k + ∂ ∂ x i ρ k u i = ∂ ∂ x j μ + μ t σ k ∂ k ∂ x j + G k - ρ ϵ - Y M ∂ ∂ t ρ ϵ + ∂ ∂ x i ρ ϵ u i = ∂ ∂ x j μ + μ t σ ϵ ∂ ϵ ∂ x j + C 1 ϵ G k ϵ k - C 2 ϵ ρ ϵ 2 k

(k: the turbulence kinetic energy, ϵ: dissipation rate, G_k: the generation of turbulence kinetic energy, Y_M: contribution of the fluctuating dilatation, μ_t: turbulent viscosity.)

Turbulent viscosity는 다음에서 볼 수 있듯이 turbulence kinetic energy와 dissipation rate의 상호 관계식으로 나타낼 수 있고 각 계수들은 다음 값을 사용하였다.

μ t = ρ C μ k 2 ϵ c 1 ϵ : 1.52, C 2 ϵ : 1.92, C μ : 0.09

The Reynolds stress는 다음 식을 통해 계산되었다

- ρ u i' u j' ¯ = μ t ∂ u j ∂ x i + ∂ u i ∂ x j

3.3 해석 조건

본 해석은 압축성 난류 유동에 대한 비정상상태의 유동해석을 진행하였다. 해당 기체는 수소(hydrogen)를 사용하였으며, 난류 모델은 standard k-ε model을 사용하였다. 고압 용기에서 분출하는 압축 수소를 모사하기 위해서 전산 유체역학 상용프로그램인 Ansys Fluent ver 18. 2를 사용하였으며 해석영역은 Ansys workbench의 design modeler 및 mesh를 통해 모델링하였고 모델링 및 mesh 형상을 Fig. 2에 나타내었다. 격자는 해석의 안정적인 격자인 square mesh로 구성하였다. 해석의 신뢰도를 위해 residual value 값은 1×10^-6 이하 값에서 수렴성을 판단하였으며 매 time step 당 20회 이상 반복계산을 수행하여 해석의 정확성을 얻었다. 수소 저장 탱크에서 수소 배출(discharge) 수치해석은 실험값¹⁴⁾과 비교를 통해 타당성을 검증하였다. 실험값의 배출 조건¹⁴⁾은 Table 3과 같다.

Fig. 2.

Modeling of storage tank

Table 3.

Hydrogen discharge condition

4. 결과 및 고찰

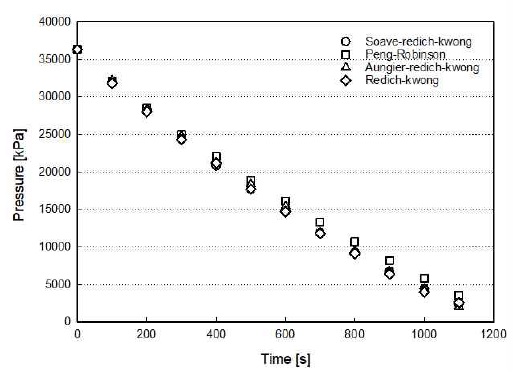
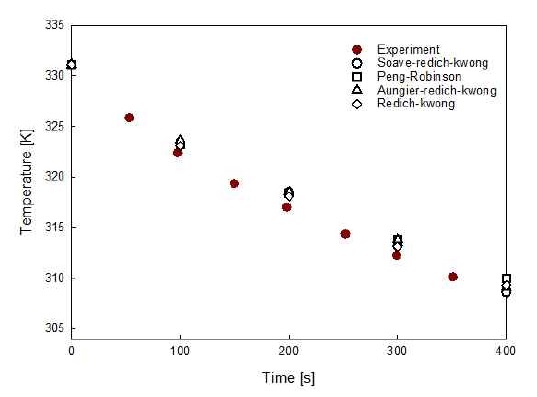
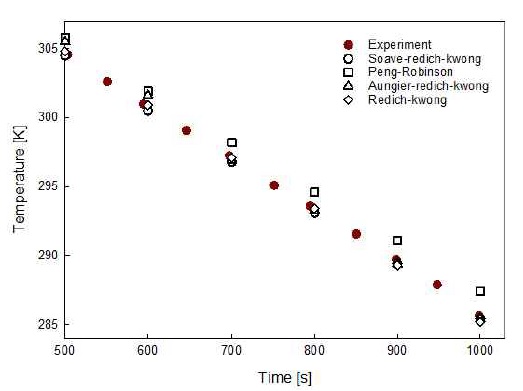
주어진 압축 수소 탱크의 배출조건에 따라(Table 3) 시간의 경과에 따른 압축 수소의 압력 및 온도 변화를 예측하기 위해 수치 해석을 진행하였고 실험값¹⁴⁾의 결과와 수치 해석의 결과를 비교하여 수치 해석 방법의 타당성을 검증하였다. 36.3 MPa 초기 압력과 331 K 초기 온도 상태의 가압수소는 약 1,100초 후 배출 시간의 경과 후 내부 압력이 2.5 MPa에 도달하였고 이 조건을 토대로 gas model에 대한 수치 해석을 진행하였다. 주어진 조건에서 압축된 수소가 배출됨에 따라 내부의 압력은 일률적으로 낮아지는 것을 Fig. 3에서 확인할 수 있다. 모델별 계산의 검증을 위해 실험값의 시간별 온도값과 해석의 시간별 온도값을 비교하여 오차를 계산하였다. 약 1,100초 후 배출 시간의 경과 후 내부 압력이 2.5 MPa에 도달하는 실험값과 비교했을 때 gas model별로 실험값과 다소 오차가 발생됨을 보인다. 그중 Redich-Kwong 모델이 가장 작은 오차가 발생함을 Tables 4, 5에서 보여준다. 또한 주어진 조건에서 압축된 수소가 배출됨에 따라 내부의 온도가 감소하는 변화를 Figs. 4, 5에서 볼 수 있다. 온도의 감소변화에 따라 초기(400초 미만)에서는 상대적으로 많은 온도 감소의 양상을 보이다가 후반(500초 이후)에는 다소 일정한 온도 감소 양상을 보이는 것을 확인할 수 있다. 이와 같은 거동의 변화 때문에 gas model에 따라 초기에는 실험값과 약 0.5% 미만의 차이를 보이나 후반에는 다소 작아진 약 0.2% 미만의 차이를 보인다. 초기에는 Soave-redich-kwong 모델과 Redich-kwong 모델이 실험값과 가장 작은 오차를 보인 반면 후반에는 Redich-Kwong이 가장 작은 오차를 보인다. 실험값의 압력 및 온도 변화의 값 비교를 통해 전체적으로 Redich-Kwong 모델이 가장 작은 오차를 보였다.

Fig. 3.

Pressure distribution of hydrogen tank with gas model

Table 4.

The averaged deviations of pressure between experimental and numerical results

Table 5.

The averaged deviations of pressure between experimental and numerical results during discharging time

Fig. 4.

Temperature distribution of hydrogen tank distribution with gas model (initial state)

Fig. 5.

Temperature distribution of hydrogen tank distribution with gas model (developed state)

5. 결 론

본 연구에서는 Type Ⅲ 수소 저장 탱크를 대상으로 고압 수소의 배출조건에서 저장 탱크의 내부 변화(압력, 온도)를 수치적으로 모사하였다. 수소 가스 모델(gas model)에 따른 수치 해석 결과값을 실험값과 비교하였고 값의 차이를 정량적으로 분석하였다. 주어진 배출조건에서 실험값(온도, 압력값)과 비교를 통해 전체적으로 Redich-Kwong의 가스 모델이 가장 작은 오차를 보임을 알 수 있었다. 본 해석 방법론은 향후 진행될 다양한 타입의 수소 저장 탱크별 수소 주입 및 배출조건별 수소 거동 분석 연구에 이용될 것으로 보인다. 나아가 수소 배출조건에 따른 수소의 거동 분석과 이에 따른 저장 탱크의 구조적 영향성 연구에 활용될 것으로 예상된다.

Acknowledgments

본 연구는 국토교통부 철도기술연구개발사업의 연구비 지원(20RTRP-B146008-03)에 의해 수행되었습니다.

References

S. H. Hong, J. S. Bae, C. Yim, Y. S. Na, and M. Y. Song, “Fabrication and hydrogen storage property of eutectic Mg-Ni based alloy powder”, Trans Korean Hydrogen New Energy Soc, Vol. 17, No. 2, 2006, pp. 174-180.
K. S. Kim, G. D. Lim, and D. H. Lee, “Combustion emission characteristics on the effect of secondary air injection in model gas turbine combustor”, J. Ocean Eng. Technol., Vol. 14, No. 3, 2000, pp. 84-89.
J. H. Lee, S. W. Kim, and H. K. Yoon, “Analysis on temperature change of super changer for the reduction of auto exhausts gas”, J. Ocean Eng. Technol., Vol. 27, No. 1, 2013, pp. 109-114. [https://doi.org/10.5574/KSOE.2013.27.1.109]
J. Seok, S. M. Jeong, J. C. Park, and J. K. Paik, “CFD simulation of methane combustion for estimation of fire and explosion in offshore plant”, J. Ocean Eng. Technol., Vol. 27, No. 2, 2013, pp. 59-68. [https://doi.org/10.5574/KSOE.2013.27.2.059]
H. J. Cho, S. H. Kim, and J. Choi, “Study of temperature dynamic characteristics of various control methods for MGO chiller system”, J. Ocean Eng. Technol., Vol. 33, No. 2, 2019, pp. 139-145. [https://doi.org/10.26748/KSOE.2019.005]
S. S. Ahn and H. S. Ko, “Analysis of density distribution for hydrogen flow using three-dimensional digital speckle tomography”, Trans Korean Hydrogen New Energy Soc, Vol. 16, No. 3, 2005, pp. 253-261.
B. H. Park, “Simulation of temperature behavior in hydrogen tank during refueling using cubic equations of state”, Trans Korean Hydrogen New Energy Soc, Vol. 30, No. 5, 2019, pp. 385-394. [https://doi.org/10.7316/KHNES.2019.30.5.385]
H. W. LEE, D. H. OH, and Y. J. SEO, “Prediction of changes in filling time and temperature of hydrogen tank according to SOC of hydrogen”, Trans. of Korean Hydrogen and New Energy Society, Vol. 31, No. 4, 2020, pp. 345-350. [https://doi.org/10.7316/KHNES.2020.31.4.345]
Chungnam Techno Park, “Report on technology roadmap for hydrogen industry in Chungnam region”, Chungnam Techno Park, 2017.
O. Redlich and J. N. S. Kwong, “On the thermodynamics of solutions. V. An equation of state. Fugacities of gaseous solutions”, Chemical Reviews, Vol. 44, No. 1, 1949, pp. 233-244. [https://doi.org/10.1021/cr60137a013]
G. Soave, “Equilibrium constants from a modified Redlich-Kwong equation of state”, Chemical Engineering Science, Vol. 27, No. 6, 1972, pp. 1197-1203. [https://doi.org/10.1016/0009-2509(72)80096-4]
R. H. Aungier, “A fast, accurate real gas equation of state for fluid dynamic analysis applications”, J. Fluids Eng., Vol. 117, No. 2, 1995, pp. 277-281. [https://doi.org/10.1115/1.2817141]
D. Y. Peng and D. B. Robinson. “A new two-constant equation of state”, Ind. Eng. Chem. Fundamen., Vol. 15, No. 1, 1976, pp. 59-64. [https://doi.org/10.1021/i160057a011]
J. Guo, J. Yang, Y. Zhao, X. Pan, L. Zhang, L. Zhao, and J. Zheng, “Investigations on temperature variation within a type III cylinder during the hydrogen gas cycling test”, Int. J. Hydrogen Energy, Vol. 39, No. 25, 2014, pp. 13926-13934. [https://doi.org/10.1016/j.ijhydene.2014.03.097]