슬로싱 거동을 고려한 극저온 저장용기의 구조 안전성 평가
2025 The Korean Hydrogen and New Energy Society. All rights reserved.
Abstract
Cryogenic vessels are used to store liquid hydrogen at 20 K. During transportation, however, structural safety concerns arise due to sloshing-induced impact pressure. This study evaluated the sloshing behaviors in a vertical vacuum-jacketed vessel through multiphase fluid flow and fluid structure interaction (FSI) analysis. When the inner vessel was 50% filled with liquid nitrogen and subjected to an acceleration of 12 m/s2, the maximum pressure of 6,340 Pa was obtained from the multiphase fluid flow analysis. The FSI analysis revealed that the maximum stress at rod connection was 242 MPa, exceeding allowable strength. To address this issue, a case study on increasing the rod’s diameter showed that the rod’s diameter of 6 mm reduced the maximum stress to 111 MPa, ensuring it remained within the allowable strength.
Keywords:
Cryogenic storage vessel, FSI analysis, Multiphase fluid flow analysis, Sloshing, Structural safety키워드:
극저온 저장용기, 유체-구조 연성 해석, 다상 유동 해석, 슬로싱, 구조 안전성1. 서 론
세계적으로 환경 문제가 대두됨에 따라 탄소 배출이 없는 수소를 에너지원으로 활용하기 위한 연구가 활발히 이루어지고 있으며 특히 에너지 소실률이 높은 수소의 특성에 따라 저장 방식에 대한 연구가 주를 이루고 있다1). 그 방식은 저장되는 수소의 상에 따라 고압 기체, 액체 및 고체로 분류된다1,2). 다른 방식 대비 액체 형태의 저장 방식은 높은 에너지 밀도로 대용량 저장 및 운송을 가능하게 하며 700 bar로 저장되는 기체 수소 저장 방식과 비교하여 대기압 수준의 낮은 압력에서 운용되기 때문에 폭발 위험성이 낮은 장점도 가지고 있다3). 그러나 액체 수소의 저장을 위하여 20 K (-253℃) 이하의 매우 낮은 온도가 유지되어야 하므로 이중 진공 단열 저장용기가 필요하고 운송 과정 중 발생하는 슬로싱(sloshing) 현상으로 저장용기의 구조 안전성에 문제가 발생할 수 있다4,5). 슬로싱은 저장용기 내에 기체 및 액체의 섞이지 않는 두 개의 상에 의하여 나타나는 자유표면이 외부 동하중에 의해 움직이는 현상이다. 이는 액체 수소용 이중 진공 단열 저장용기 내벽에 지속적인 충격 하중을 가하게 되며 특히 단열을 위하여 특수하게 제작된 지지 구조물의 파손을 야기할 수 있다. 따라서 저장용기 내 슬로싱 현상의 동적 특성을 파악하고 그로 인해 발생하는 문제에 대한 구조 설계안이 필요하다.
Song 등6)은 슬로싱 거동과 발생하는 충격 압력을 평가하기 위해 다양한 실험을 수행하였으며 충격 압력은 유동 속도 변화에 따른 국소 에너지에 크게 영향을 받는다고 보고하였다. 그러나 실험을 통한 슬로싱 거동의 평가는 비용적인 문제와 더불어 계측 장비의 설치 문제로 단순한 형상의 저장용기를 사용해야만 하는 제약이 따를 수밖에 없다. Yang과 Kim7)은 CIP-combined unified procedure 및 tangent of hyperbola for interface capturing 기법을 적용하여 좌우 반복 및 횡운동에 대한 슬로싱 현상을 수치적으로 모사하였다. 수치 해석 결과는 실험으로 계측된 거동과 유사하였고 내벽에 가해지는 충격 하중에 의한 압력을 비교적 정확하게 예측할 수 있음을 확인하였다. Liu 등8)은 슬로싱 거동을 Reynolds averaged Navier-Stokes (RANS), large Eddy simulation (LES) 및 very large Eddy simulation (VLES) 등과 같은 난류 및 층류 모델을 이용한 유동 해석으로 모사하여 이를 실험 결과와 비교하였다. 실험 결과를 가장 유사하게 모사한 난류 모델은 많은 계산 비용이 요구되는 LES이지만 RANS와 VLES 난류 모델도 적은 계산 비용으로도 비교적 유사한 결과를 보여주어 슬로싱 거동을 평가하는 모델로 효과적임을 보고하였다. 한편 외부 동하중에 의하여 발생한 슬로싱이 저장용기의 구조 안전성에 미치는 영향을 분석한 연구는 Choi 등9)에 의하여 수행되었다. 연료전지를 사용하는 상용 트럭의 액체수소 탱크에 대하여 International Organization for Standardization (ISO) 규격에 따른 관련 표준 코드를 기반으로 구조 해석이 수행되었다. 상용 트럭의 세 가지 운전 조건에 따라 탱크 내벽에 가해지는 최대 응력의 크기는 서로 유사하였으나 가속 운전 조건에서 탱크와 차량을 연결하는 지지 구조물에 178 MPa의 높은 응력이 발생하여 지지 구조물에 대한 구조 안전성 평가가 필요하다고 제시하였다. Kim 등3)은 liquefied natural gas 화물 격납 시스템에서 나타나는 슬로싱 거동을 평가하기 위하여 각 시간대별 유동에 의한 구조의 반응을 결합한 접근법으로 천이 해석을 수행하였다. 이를 통하여 0.0067초에서 내벽에 가해지는 최대 응력의 값을 계산하였다.
상기 연구 사례들은 슬로싱 거동을 유체-구조 연성(fluid structure interaction, FSI)으로 모사하는 과정에서 액체 수소용 저장용기 내에서 나타날 수 있는 구조적 거동의 과도 현상을 충분히 다루지 못하고 있다. 특히 적재한 차량의 급정거로 인하여 발생하는 슬로싱 현상은 충격 하중을 유발하여 저장 용기의 구조적 안전성에 부정적인 영향을 미칠 수 있으며 이는 저장용기 지지 구조의 신뢰도를 저하시킬 수 있다.
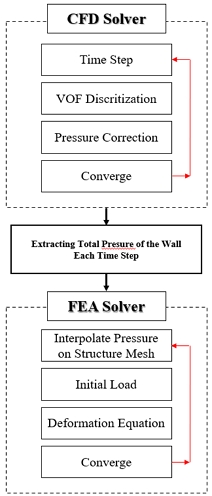
본 연구에서는 수직형 액체 수소용 이중 진공 단열 저장용기를 상용 해석 프로그램인 ANSYS Fluent (Ansys, Canonsburg, PA, USA)를 활용하여 벽면에서 높은 유동 예측 신뢰도를 보이는 k-ω SST 난류 모델10)이 적용된 volume of fluid (VOF) 기법을 활용한 기체-액체 상의 다상 유도 과도 수치 해석 모델을 구축하였다. 저장용기의 운송 조건이 고려된 외부 동하중에 의한 슬로싱 거동을 해석적으로 평가하였고 이를 Yang과 Kim의 실험 결과7)와 비교하여 구축한 수치 해석 모델의 정확도를 분석하였다. 아울러 과도 수치 해석 모델을 반영한 FSI 해석을 수행하여 시간대별 유동에 의한 저장용기 내벽의 작용 압력을 구하였고 작용 압력이 저장용기 지지물에 미치는 영향을 구조 강도 관점에서 고찰하였다.
2. 수치 해석 모델 및 방법
2.1 다상 유동 해석
수직형 액체수소용 이중 진공 단열 저장용기 내에서 발생하는 슬로싱 거동을 모사하기 위하여 상용 해석 프로그램인 ANSYS Fluent를 활용하였다. 작동유체는 기체 및 액체 질소로 하였으며 저장용기 내부에서 서로 섞이지 않는 기체-액체 상이 공존하며 외부 동하중에 의하여 자유표면이 움직이는 슬로싱 거동은 k-ω SST 난류 모델이 적용된 VOF 기법11) 기반 다상 유동 해석(multiphase fluid flow analysis)으로 추정하였다. VOF 기법은 경계면의 곡률 계산에 일부 한계가 있으나 복잡한 형상의 경계면에도 적용이 가능하기 때문에 많은 공학적 문제에 활용되고 있다12).
다상 유동 해석의 연속방정식 및 운동량방정식은 다음과 같다13).
| (1) |
| (2) |
여기서 ρ는 혼합 상의 밀도, t는 혼합 상의 시간, 는 혼합 상의 속도 벡터, μ는 점성계수, p는 혼합 상의 압력, 는 중력가속도 그리고 F는 외력을 의미하며 표면장력이 포함되어 있다. μt는 난류 점성계수로 RANS 방정식에서 발생하는 레이놀즈 응력항을 처리하기 위해 적용된 비례상수이다.
기체 및 액체 상을 각각 아래첨자 g와 l이라고 하고 상기한 연속방정식과 운동량방정식을 부피 분율(volume fraction)로 나타내면 다음과 같다.
| (3) |
여기서 α는 부피 분율이며 섞이지 않는 각 상의 부피를 전체 부피로 나눈 값이다. 저장용기 내에서 기체와 액체 상의 부피 분율 합은 1이 되어야 하므로 제약 조건을 다음과 같이 표현할 수 있다.
| (4) |
2.2 FSI 해석
슬로싱이 저장용기의 구조물에 미치는 영향을 분석하기 위하여 FSI 해석 기법을 활용하였다. FSI는 일반 구조 해석 지배방정식과 마찬가지로 구조에 가해진 하중으로 인한 변형을 수치적으로 해결하는 유한 요소법14,15)을 참고하였고 단방향 결합 방식을 채용하여 슬로싱 거동에 의한 저장용기 내벽에 발생하는 압력을 하중 경계조건으로 적용하였다.
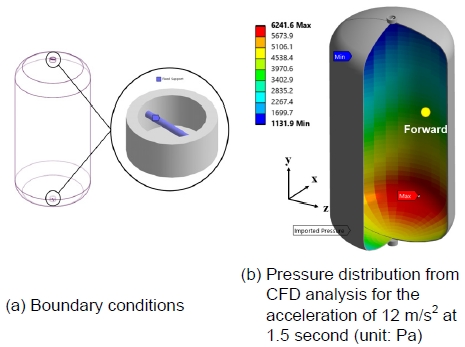
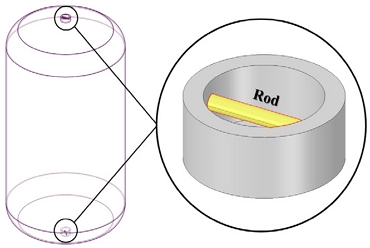
해석 대상체는 Fig. 1과 같이 크리오스에서 개발 중인 수직형 액체수소용 이중 진공 단열 저장용기로 sus316l로 제작된 내부 저장용기(inner vessel)는 상부, 하부 지지 구조와 rod로 연결되어 외부 저장용기(outer vessel)에 고정되어 있다. 열 침투에 의한 열전달 효과를 최소화하기 위하여 rod 단면을 가능한 작게 하였으나 저장용기의 이송 시 발생하는 동하중에 의한 작동유체의 슬로싱 거동으로 rod 단면과 지지구조의 연결부에 높은 응력이 발생할 수 있다. 따라서 파손 위험성을 피하기 위하여 구조 강도의 관점에서 설계 검토가 요구되고 있다.
Configuration of inner vessel and top- and bottom-supported structures in vertical vacuum jacketed storage vessel
수직형 액체수소용 이중 진공 단열 저장용기의 이송 중 발생하는 슬로싱이 저장용기 지지물에 미치는 영향을 구조 강도 관점에서 평가하기 위하여 Fig. 2와 같은 단방향 FSI 해석을 수행하였다. 저장용기 내부에서 서로 섞이지 않는 기체-액체 계면의 자유표면 움직임을 2.1절에서 설명한 VOF 기법 기반 다상 유동 해석으로 평가하고 과도 해석을 통해 이송 시 나타나는 시간 단계별 슬로싱 거동에 의한 저장용기 내벽의 압력 변화를 계산한 후 이를 구조 해석의 경계조건으로 활용하였다. 저장용기 내벽에 작용하는 압력 변화가 지지 구조에 미치는 영향을 분석하기 위하여 구조 해석을 실시하였으며 저장용기의 FSI 해석 모델의 정확성과 계산 시간을 절충한 단방향 결합 방식이 활용되었다16).
3. 다상 유동 해석 결과
3.1 수치 해석 모델의 검증
본 연구에서 제안한 k-ω SST 난류 모델이 추가된 VOF 기법 기반 다상 유동 해석 모델의 검증은 Yang과 Kim7)이 제시한 실험 결과와 비교를 통하여 이루어졌다. Fig. 3은 실험에 적용된 800×500 mm 크기의 직사각형 저장용기로 상온의 물을 충진율 50%로 채운 상태에서 슬로싱 실험이 이루어졌으며 저장용기 바닥에서 115 mm 높이의 내벽에 설치된 압력 센서를 이용하여 압력값을 계측하였다7). 저장용기 내의 유체는 슬로싱에 의하여 가로 방향으로 진동하며 이때 변위 δ는 시간 t에 따라 아래와 같이 나타낼 수 있다.
| (5) |
여기서 a는 진폭, b는 진동수이며 이들은 각각 실험 조건인 진폭 0.02 m 및 저장용기의 고유진동수 5.388 rad/s로 설정되었다.
진동하는 저장용기 내의 유체는 저장용기의 가로 및 세로 방향인 x 및 y 방향의 가속도 성분을 갖게 되며 x 방향의 가속도는 식 (2)의 x 방향 중력가속도 항에 대입하였고 y 방향의 가속도는 중력가속도인 9.81 m/s2를 적용하였다.
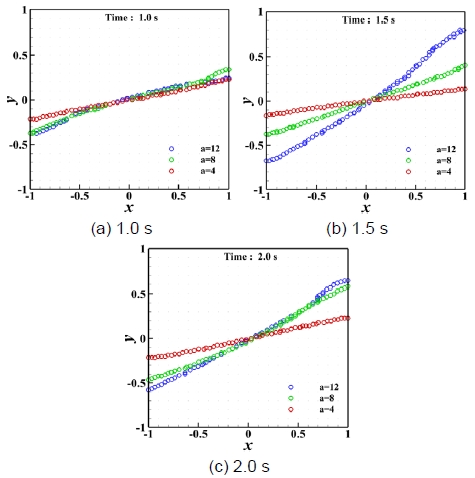
식 (3)으로 얻어진 하나의 격자에 포함되는 액체와 기체의 면적과 부피를 식 (4)에 대입하여 부피 분율 α를 구할 수 있다. 이때 α가 0.5가 되는 곳에서 두 상의 경계층이 나타나므로 슬로싱에 의한 유체의 자유표면을 해당 α의 위치로 추출하였으며 이는 Fig. 4와 같다. 한 주기의 첫 번째 및 네 번째 분기의 자유표면 위치를 저장용기의 가로 및 세로 길이로 각각 무차원화한 x 및 y로 표시하였다. 해석으로 얻어진 자유표면 위치는 Yang과 Kim7)의 실험 결과와 유사하며 중력에 의한 유체 붕괴와 벽면 충돌 이후 발생하는 뭉쳐있던 유체가 액적으로 분산되는 현상까지 효과적으로 모사되고 있음을 확인할 수 있다.
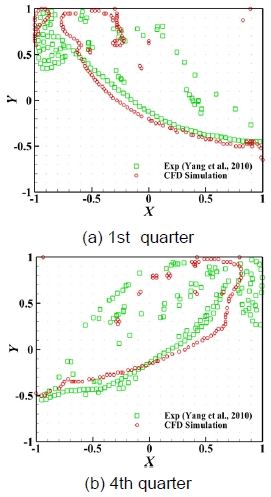
Free-surface profiles obtained by proposed model and experimental results7) at 1st and 4th quarters of one cycle
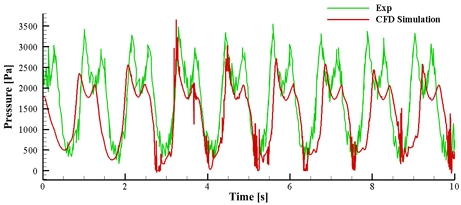
한편 압력 센서 위치에서 나타나는 압력값은 식 (1)과 (2)로부터 속도-압력 연성 해석을 통해 구할 수 있으며 이를 시간 단계별로 추출하면 Fig. 5와 같다. 이를 Yang과 Kim7)의 실험 결과와 비교하면 초기 과도 구간(initial transient period)을 제외하고 전체적인 경향성이 일치하는 것을 알 수 있다. 이를 통해 k-ω SST 난류 모델이 적용된 VOF 기법 기반 다상 유동 해석 모델이 진동하는 저장용기 내의 유체의 거동을 비교적 정확하게 모사하고 있다고 판단된다.
3.2 대상체 및 해석 조건
대상체는 앞서 2.2절에서 설명한 수직형 진공 단열 저장용기의 내부 저장용기(inner vessel)이며 내부 저장용기의 유체에서 발생하는 슬로싱 현상을 모사하기 위하여 VOF 기법 기반 다상 유동 해석이 수행되었다. Fig. 6(a)는 내부 저장용기 유동장의 격자 모델로 총 308,448개의 격자로 구성되었으며 작동유체는 액체 질소로 물성치는 Table 1과 같다.
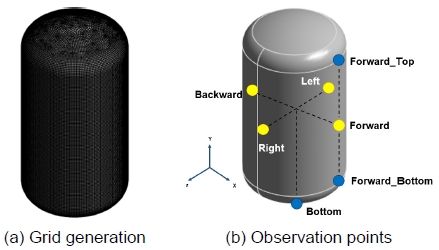
Grid generation and observation points of fluid flow in inner vessel of vertical vacuum-jacketed storage vessel
슬로싱 현상은 저장용기를 탑재한 차량이 각각 약30, 60 및 90 km/h의 속도로 이동하는 중에 2초간 등가속도로 급정거하는 조건으로 상정하여 수평 방향의 가속도인 4, 8 및 12 m/s2를 고려하였다. 슬로싱 현상으로 나타나는 액체 질소의 동적 거동과 벽면에 작용하는 압력의 변화를 평가하기 위하여 벽면에 점착 단열 조건(no-slip adiabatic)을 부여한 상태에서 총 5초 동안의 과도 해석(transient analysis)이 수행되었다. 과도 해석 시 내부 저장용기 전, 후면 및 양측의 압력 변화를 파악하기 위해 최초 자유수면 높이를 기준으로 설정된 지점인 Forward, Backward, Left, Right와 정수압과 저장용기 상부 및 하부의 작용 압력을 평가하기 위한 지점인 Bottom, Forward_Top 그리고 Forward_Bottom을 Fig. 6(b)에 표시하였다. 관측 지점(observation points)에서의 작용 압력의 변화를 계산하였으며 수위가 낮은 경우 슬로싱에 의한 급격한 파동의 변화로 압력의 변동성이 증가하기 때문에 충진율은 50%로 설정하였다17).
3.3 해석 결과
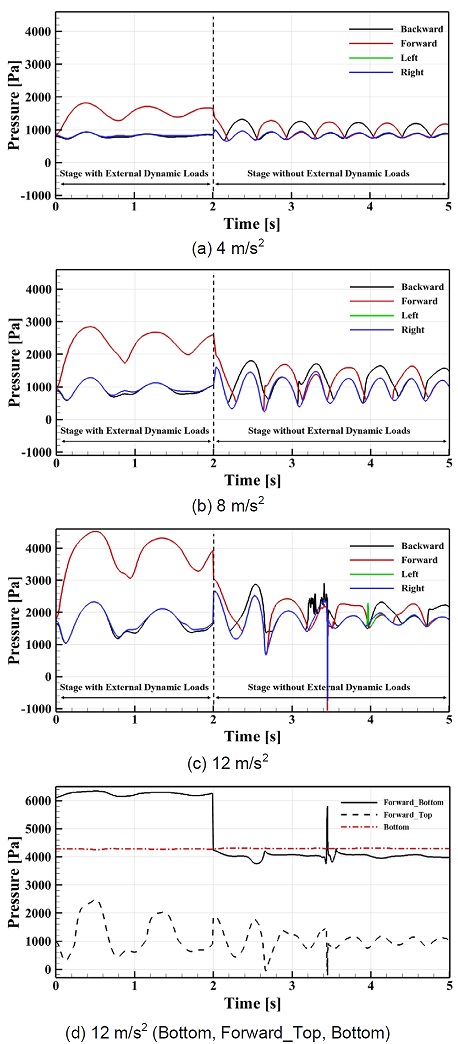
저장용기를 탑재한 차량이 등속 이동하는 중에 2초간 등가속도로 급정거하는 조건을 포함한 총 5초 동안 각 관측 지점인 Forward, Backward, Left 및 Right에서의 압력 값을 Fig. 7(a)-(c)에 나타내었다. 이때 등가속도로 급정거하는 2초 동안은 외부 동하중 작용 구간(stage with external dynamic loads)으로, 이후 3초 동안을 외부 동하중이 작용하지 않는 구간(stage without external dynamic loads)으로 나누었다. 외부 동하중이 작용하는 구간에서 내부 저장용기 벽면에 발생하는 압력은 관측 지점 중 Forward에서 가장 높게 나타났다. 모든 사례에서 압력 변화의 경향이 비슷한 모습을 보여주었으며 가속도의 증가에 따라 발생하는 압력은 크기에 비례하여 가속도가 4, 8 및 12 m/s2에서 최대 압력은 각각 1,820, 2,848 및 4,525 Pa이다. 반면 Backward, Left 및 Right 지점에서의 압력은 Forward에서 측정된 압력에 비해 상대적으로 낮았다. 외부 동하중이 작용하지 않는 시점 이후 Forward에 나타나는 압력이 급격하게 감소하였고 이후 가속도가 4, 8 m/s2의 경우 주기성을 띄는 반복적인 슬로싱 현상이 발생하였다. 이때 모든 관측 지점에서 비슷한 주파수와 압력 값이 나타났다. 반면 가속도가 12 m/s2인 경우 다른 사례와 다르게 불규칙적인 압력 변화가 나타나며 3.4초 시점에 불규칙한 압력 변동이 발생하였다. 또한 외부 동하중인 가속도의 크기가 클수록 주기가 길어지는 경향이 나타났는데 이는 유체에 가해진 하중이 클수록 관성이 증가하여 육체가 벽에 부딪혔음에도 점성과 변형에 의하여 벽 주변에 오래 머물기 때문인 것으로 보인다. 한편 가속도가 12 m/s2에서 내부 저장용기의 Bottom과 관측 지점 중 가장 큰 압력이 작용하는 Forward의 상부 및 하부인 Forward_Top과 Forward_Bottom에서의 압력은 Fig. 7(d)와 같다. Forward_Top에서의 작용 압력은 외부 동하중 작용 구간에서 최대 2,495 Pa이며 Forward_Bottom에서는 작용 압력이 최대 6,340 Pa으로 상승하여 내부 저장용기에서 가장 높은 압력이 작용하고 있음을 알 수 있다. 또한 Bottom에서 나타나는 평균 정수압인 4,298 Pa 대비 47.5% 더 높은 값이 나타나는 것을 확인하였다. 이를 통해 외부 동하중에 의하여 유체가 몰리게 되면서 기존 정수압보다 더 큰 압력을 발생시키는 것을 알 수 있다.
외부 동하중이 작용하는 구간에서 시간 구역에 따른 자유표면 위치를 내부 저장용기의 가로 및 세로 길이로 각각 무차원화하여 각 가속도 조건에 대하여 나타내면 Fig. 8과 같다. 1초 구간에서는 자유표면 위치가 가속도와 무관하게 유사하며 최대 압력이 나타나는 1.5초 구간에서는 가속도의 크기와 자유표면의 기울기가 비례하는 경향을 보이고 가속도가 12 m/s2에서 가장 급격한 자유표면의 기울기가 나타났다. 이후 외부 동하중이 멈추는 2초 시점에서 가속도가 4 m/s2인 경우를 제외한 나머지 가속도 조건에서 자유표면의 기울기는 유사하였다. 따라서 외부 동하중에 의한 가속도가 증가할수록 자유표면의 기울기가 커지는 경향을 확인할 수 있다.
4. FSI 해석 결과
4.1 하중 경계조건
수직형 이중 진공 단열 저장용기의 내부 저장용기는 상하부의 지지 구조와 rod에 의하여 외부 저장용기에 연결되어 있다. Rod는 내부 저장용기의 하중을 수용하며 외부 열 침입에 의한 열전달을 막기 위하여 작은 단면적을 가지고 있어 슬로싱으로 인해 발생하는 동적 하중에 의하여 구조적으로 취약해질 수 있다. 단방향 FSI 해석16)을 통해 슬로싱에 의하여 유체의 동적 하중이 내부 저장용기에 미치는 영향을 고려하여 rod에 가해지는 응력을 평가하였다.
Fig. 9는 구조 해석에서 적용된 전처리 과정으로 Fig. 9(a)와 같이 상하부 지지 구조의 rod를 고정하는 경계조건을 부여하였고 슬로싱에 의한 영향만을 고려하기 위하여 내부 저장용기의 자중은 고려하지 않았다. 슬로싱에 의한 내부 저장용기에 가해지는 하중조건은 3절의 다상 유동 해석으로 얻어진 시간 경과에 따른 압력 분포로 부여하였다. Fig. 9(b)는 가속도가 12 m/s2인 경우 과도 해석이 진행된 1.5초 시점의 압력 분포의 사례로써 각 시점의 압력 분포를 하중 조건으로 적용하여 Rod에 발생하는 응력을 계산하였다.
4.2 해석 결과
Fig. 10은 Fig. 9의 하중 경계조건에서 FSI 해석으로 얻어진 하부 지지 구조의 rod 연결부에 발생하는 von Mises 응력 분포이다. Rod가 지지 구조와의 연결부에서 응력이 집중되었으며 이때 최대 응력은 242 MPa 수준이다. 지지 구조 및 rod의 사용 소재인 SUS316L은 고압가스용 저장탱크 및 압력용기 제조의 시설・기술・검사 기준18)에 따라 77 K에서 허용 강도를 114 MPa로 제한하고 있어 슬로싱에 의해 rod에 작용하는 응력이 사용 소재의 허용 강도를 초과하고 있다. 따라서 각각의 가속도를 고려한 다상 유동 해석의 과도 해석으로 얻어진 슬로싱에 의한 내부 저장용기의 압력 분포로부터 rod에 작용하는 von Mises 응력을 고찰하였다.

Stress distribution at connection of rod and bottom-supported structure for the acceleration of 12 m/s2 at 1.5 second (unit: MPa)
Fig. 11은 5초간 상하부 지지 구조의 rod에 작용하는 최대 von Mises 응력의 변화를 가속도별로 나타낸 결과이다. 상부 지지 구조 rod의 경우 Fig. 11(a)와 같이 등가속도로 급정거하는 2초 동안 외부 동하중 작용 구간 중 가속도가 12 m/s2에서 최대 78 MPa, 8 m/s2에서 45 MPa, 4 m/s2에서 28 MPa 수준으로 응력이 발생하였으며 외부 동하중이 작용하지 않는 구간에서는 큰 변화 없이 유사하게 나타났다. 슬로싱에 의한 구조 강도 측면에서 상부 지지 구조 rod는 안전하다고 판단된다. 한편 하부 지지 구조 rod의 경우 Fig. 11(b)와 같이 발생하는 최대 응력이 가속도의 크기에 따라 큰 폭으로 증가하였다. 외부 동하중 작용 구간에서 가속도가 12 m/s2인 경우 1.5초 시점에서 232 MPa의 응력이 나타났으며 외부 동하중이 작용하지 않는 구간에서는 작용 응력이 75 MPa로 급격히 감소하였다. 가속도가 8 m/s2인 경우 작용 응력은 각 구간별로 128 MPa 및 50 MPa로 나타났고 가속도가 가장 낮은 4 m/s2에서는 각 구간별로 65 MPa 및 35 MPa의 반복 응력이 발생하였다. 사용 소재인 SUS316L의 허용 강도가 114 MPa이므로 가속도가 4 m/s2인 경우를 제외하고 슬로싱에 의한 하부 지지 구조 rod는 요구되는 구조 강도를 만족하지 못하였다. 따라서 rod의 단면적을 증가시키기 위한 형상 설계 변경이 요구된다.
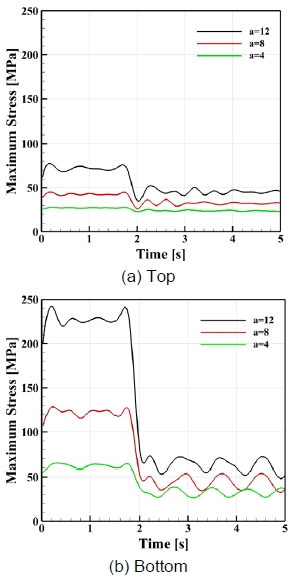
Maximum stress occurred in the rods of top- and bottom-supported structures regarding to accelerations over the time
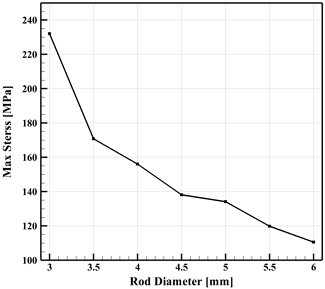
하부 지지 구조 rod의 지름을 증가시키는 사례 연구를 실시하였다. 사례 연구에서 기존 rod의 지름 3 mm를 6 mm까지 0.5 mm 간격으로 증분하였으며 가속도가 12 m/s2인 경우 유체-구조 상호작용 해석 시 높은 응력이 발생하는 1.5초 시점까지의 하중 경계조건을 부과하고 Rod에 작용하는 최대 응력을 계산하였다. Fig. 12는 사례 연구의 결과로 기존 rod의 지름인 3 mm에서 발생한 232 MPa의 최대 응력은 지름이 3.5 mm로 증가한 경우 171 MPa로 약 29.4%가량 크게 감소하였다. 이후 rod의 지름이 6 mm까지 증가하면 최대응력은 111 MPa로 KGS AC111 2024 기준17)에서 규정하는 SUS316L의 허용 강도를 충족함을 확인하였다.
5. 결 론
본 연구에서는 수직형 액체 수소용 이중 진공 단열 저장용기에서 발생하는 슬로싱 거동을 난류 모델이 적용된 VOF 기법을 활용한 다상 유도 과도 수치해석으로 평가하였으며 과도 수치 해석 모델을 반영한 FSI 해석으로 작용 압력이 저장용기 지지물에 미치는 영향을 구조 강도 관점에서 고찰하였다. 얻어진 결과는 다음과 같다.
- 1) ANSYS Fluent를 활용한 k-ω SST 난류 모델이 적용된 VOF 기법 기반 다상 유동 해석 모델은 Yang과 Kim7)의 실험 결과와의 비교를 통해 슬로싱에 의한 유체의 거동을 비교적 정확하게 모사함을 확인하였다.
- 2) 액체 질소가 50% 충진율로 채워진 수직형 진공 단열 저장용기의 내부 저장용기에서 등가속도 운송 조건을 고려한 경우 가속도의 증가에 따라 슬로싱에 의하여 내벽에 작용하는 압력은 증가하였으며 12 m/s2의 가속도 조건에서 관측 지점인 Forward_Bottom에서의 작용 압력은 6,340 Pa으로 내부 저장용기에서 가장 높았다.
- 3) FSI 해석을 통해 가장 높은 작용 압력이 나타나는 슬로싱에 의한 하부 지지 구조와 rod에 작용하는 최대 응력은 242 MPa로 KGS AC111 2024 기준에서 규정하는 사용 소재인 SUS316L의 허용 강도인 114 MPa를 초과하였다.
- 4) 하부 지지 구조 rod의 지름을 증가시키는 사례 연구를 실시하여 기존 rod의 지름을 6 mm까지 증가시키면 최대 응력은 111 MPa로 SUS316L의 허용 강도를 충족함을 확인하였다.
Acknowledgments
본 논문은 부산광역시 및 (재)부산테크노파크 BB21 plus 사업의 지원을 받았음.
References
- Ministry of Economy and Finance, “2050 carbon neutral strategy of the Republic of Korea”, Ministry of Economy and Finance, 2020. Retrieved from https://www.korea.kr/archive/%20expDocView.do?docId=39241, .
- B. H. Park, “Simulation of temperature behavior in hydrogen tank during refueling using cubic equations of state”, Journal of Hydrogen and New Energy, Vol. 30, No. 5, 2019, pp. 385-394.
-
C. Kim, G. Kim, and H. Kim, “Analysis of domestic and foreign policy and technology trends for hydrogen industry development”, Journal of Hydrogen and New Energy, Vol. 34, No. 2, 2023, pp. 122-131.
[https://doi.org/10.7316/JHNE.2023.34.2.122]

- C. Chae, G. Im, Y. Kim, and S. Chae, “An analysis of the impact of design factors using a simulator of LH2 storage tank PRV system”, Journal of the Korean Institute of Gas, Vol. 28, No. 2, 2024, pp. 47-55.
-
S. Y. Hwang and J. H. Lee, “The numerical investigation of structural strength assessment of LNG CCS by sloshing impacts based on multiphase fluid model”, Applied Sciences, Vol. 11, No. 16, 2021, pp. 7414.
[https://doi.org/10.3390/app11167414]

-
Y. K. Song, K. A. Chang, Y. Ryu, and S. H. Kwon, “Experimental study on flow kinematics and impact pressure in liquid sloshing”, Experiments in Fluids, Vol. 54, 2013, pp. 1592.
[https://doi.org/10.1007/s00348-013-1592-5]

-
K. K. Yang and Y. H. Kim, “Numerical analysis of violent sloshing problems by CCUP method”, Journal of the Society of Naval Architects of Korea, Vol. 47, No. 1, 2010, pp. 1-10.
[https://doi.org/10.3744/SNAK.2010.47.1.001]

-
D. Liu, W. Tang, J. Wang, H. Xue, and K. Wang, “Comparison of laminar model, RANS, LES and VLES for simulation of liquid sloshing”, Applied Ocean Research, Vol. 59, 2016, pp. 638-649.
[https://doi.org/10.1016/j.apor.2016.07.012]

-
Y. Choi, J. Kim, S. Park, H. Park, and D. Chang, “Design and analysis of liquid hydrogen fuel tank for heavy duty truck”, International Journal of Hydrogen Energy, Vol. 47, No. 32, 2022, pp. 14687-14702.
[https://doi.org/10.1016/j.ijhydene.2022.02.210]

-
F. R. Menter, “Two-equation Eddy-viscosity turbulence models for engineering applications”, AIAA Journal, Vol. 32, No. 8, 1994, pp. 1598-1605.
[https://doi.org/10.2514/3.12149]

-
C. W. Hirt and B. D. Nichols, “Volume of fluid (VOF) method for the dynamics of free boundaries”, Journal of Computational Physics, Vol. 39, No. 1, 1981, pp. 201-225.
[https://doi.org/10.1016/0021-9991(81)90145-5]

- K. Lee, K. S. Yang, and C. Kang, “Fractional step method combined with volume-of-fluid method for efficient simulation of unsteady multiphase flow”, Journal of Computational Fluids Engineering, Vol. 15, No. 4, 2010, pp. 99-108. Retrieved from https://koreascience.kr/article/JAKO201015537944794.pdf, .
-
Y. J. Jang, “Comparative analysis of liquid sloshing phenomena by various numerical methods”, Journal of Computational Fluids Engineering, Vol. 25, No. 4, 2020, pp. 8-15.
[https://doi.org/10.6112/kscfe.2020.25.4.008]

-
G. Fourey, C. Hermange, D. Le Touzé, and G. Oger, “An efficient FSI coupling strategy between smoothed particle hydrodynamics and finite element methods”, Computer Physics Communications, Vol. 217, 2017, pp. 66-81.
[https://doi.org/10.1016/j.cpc.2017.04.005]

-
G. Hou, J. Wang, and A. Layton, “Numerical methods for fluid-structure interaction - a review”, Communications in Computational Physics, Vol. 12, No. 2, 2012, pp. 337-377.
[https://doi.org/10.4208/cicp.291210.290411s]

-
M. Masoomi and A. Mosavi, “The one-way FSI method based on RANS-FEM for the open water test of a marine propeller at the different loading conditions”, Journal of Marine Science and Engineering, Vol. 9, No. 4, 2021, pp. 351.
[https://doi.org/10.3390/jmse9040351]

- K. J. Kim, H. D. Seo, and D. Kim, “Characteristics of sloshing load and flow inside a tank with cylinder structures”, Journal of the Korean Society of Visualization, Vol. 21, No. 1, 2023, pp. 31-39.
- Korea Gas Safety Corporation (KGS), “Facility/technical/inspection code for manufacture of storage tanks and pressure vessels for high-pressure gases”, KGS, 2024. Retrieved from https://cyber.kgs.or.kr/kgscode.codeSearch.view.ex.do?onEngYn=F&pblcRlmCd=01&pblcMdclCd=&pblcCd=AC111_230306&stDayY=2008&stDayM=01&etDayY=2023&etDayM=04, .