수소전기차용 연료전지 시스템 최적 물 관리 열역학적 접근
2025 The Korean Hydrogen and New Energy Society. All rights reserved.
Abstract
A systematic, multicomponent model has been developed to investigate optimal water management for fuel cell electric vehicles. Water management strategies focus on manipulating thermodynamic states to provide the adequate requirements of fuel cells. A fuel cell water transfer model, a membrane humidifier model, and a compressor model are mathematically developed and solved using MATLAB to achieve an integrated thermodynamic approach based on system piping and instrumental diagrams. Each component model is validated using published experimental data with good agreement. In the air supply system, the required humidity at the fuel cell channel inlets is theoretically predicted under low heating value operating fuel cells. Subsequently, the optimal conditions of the compressor and the bypass valves are suggested to control the humidification levels of the humidifier. The results show the thermodynamic states within system in accordance with the optimal operation conditions of the component.
Keywords:
Fuel cell system, Vehicular application, Water management, Optimal operating condition, Thermodynamic approach키워드:
연료전지 시스템, 차량용, 물 관리, 최적 운전 조건, 열역학적 접근1. 서 론
1.1 배경
수소전기차는 높은 에너지 효율성과 배출가스가 없는 친환경 특성으로 인하여 미래 자동차 산업의 핵심 기술로 주목받고 있다. 그러나 수소전기차의 상용화를 위해서는 연료전지 시스템 내 복합적인 전달 현상을 이해하고 이를 바탕으로 당면해 있는 과제들을 해결할 필요가 있다. 그중에서도 물은 연료전지 스택의 효율 및 내구성에 중요한 영향을 미치는 핵심 요소이다. 특히 건조한 환경에서는 수소이온의 전달 감소로 인한 성능 저하를 유발할 수 있으며 반대로 과도하게 습한 환경에서는 응축수가 발생하여 반응물의 전달성이 감소하게 된다. 이를 해결하기 위하여 각 목적에 부합하는 구성요소 부품들이 설계되며 이 부품들은 연료전지 스택과 통합되어 시스템을 구성한다. 본 연구에서는 이러한 구성요소 부품들과 연료전지 스택 간의 물 관리에 집중하여 시스템 관점으로 최적의 운전조건을 도출하고자 한다.
1.2 선행 연구
그동안 연료전지 스택의 성능을 최대화하기 위하여 다양한 시스템 관점의 연구가 진행되었다. 이전 연구들은 구성요소 부품들의 운전조건에 따른 연료전지 스택의 성능을 확인하여 데이터를 축적하는1) 일종의 피드백 형태로 연료전지 시스템의 운전조건을 최적화하였다. 그러나 이러한 접근은 방대한 데이터와 실험값에 의존적이며 다양한 스케일의 연료전지 시스템에 적용하기에는 한계가 있다. 이후 연료전지 내부의 물 흐름과 분포를 이해하기 위한 정밀한 모델들이 개발됨에 따라2-5) 이론 기반의 예측 전략이 주목받기 시작하였다. 더불어 가습기 및 압축기와 같은 연료전지 시스템 구성요소의 개별 모델이 개발되면서6,7) 이를 통합한 시스템 차원의 접근8)이 가능해졌다.
1.3 연구 목적
본 연구에서는 차량용 연료전지 시스템을 대상으로 보다 체계적이고 구성요소 부품들과 통합된 최적의 물 관리 모델을 개발하고자 한다. 이전의 시스템 관점의 연구들과는 달리 연료전지 채널 입구의 요구 습도를 역으로 예측하고 이에 부합하도록 구성요소 부품들의 운전조건을 탐색하는 새로운 알고리즘을 제시한다. 이를 위하여 연료전지 시스템 구성요소 부품들의 내부 전달 현상을 구현 가능한 각각의 수학적 모델을 개발하였다. 유사 2차원(pseudo-two dimension) 연료전지 물 전달, 셸 앤 튜브형(shell & tube type) 막 가습기 그리고 원심류형 압축기의 이론 기반 모델링을 진행하였고 이를 통합하여 열역학적 접근의 연료전지 시스템 환경을 구축하였다.
1.4 논문 구성
시스템 설명 장에서는 차량용 연료전지 시스템의 구성요소 부품들과 역할에 대해 상세히 설명하였다. 특히 물 관리에 중요한 구성요소 부품들의 수학적 모델링은 모델 개발 장에서 제시된다. 결과 및 고찰 장에서는 각 모델의 검증과 함께 연료전지 스택의 요구 습도 변화에 따른 구성요소의 최적 운전조건을 논의하고 이를 바탕으로 연료전지 시스템의 열역학적 상태량 변화를 설명하였다. 결론 장에서는 본 연구의 핵심인 연료전지 시스템을 역공학적으로 예측 관리하는 접근 방식의 장점과 활용 가능성을 재고하였다.
2. 시스템 설명
2.1 수소전기차 시스템 piping and instrumental diagrams (P&ID) 개념 설계
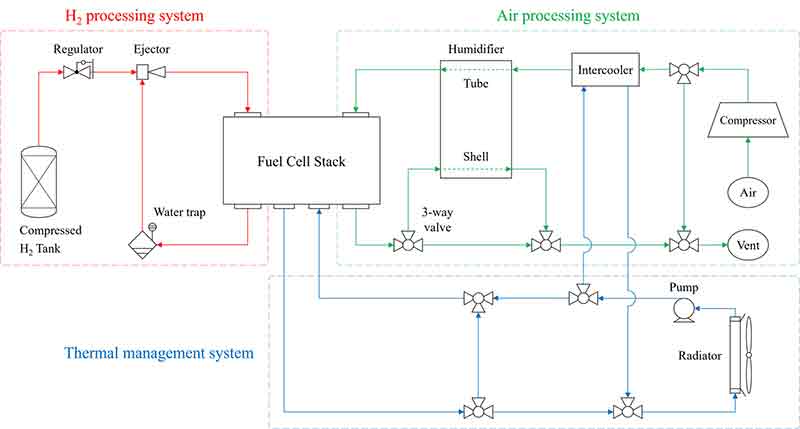
수소전기차의 핵심 구성요소는 크게 연료전지 스택, 수소공급계(H2 processing system), 공기공급계(air processing system) 그리고 열관리계(thermal management system)로 구분할 수 있다9). 연료전지 스택은 연료전지의 전기화학적 반응이 일어나는 중심 요소로 수소와 공기(산소)의 전기화학 반응을 통해 전력을 제공한다. 수소공급계는 수소탱크에서부터 연료전지 스택에 수소를 공급하기까지의 역할을 담당하는 구성요소 부품들의 총칭이며 공기공급계는 외부 공기로부터 연료전지 스택에 공기가 공급되기까지의 역할을 담당하는 구성요소 부품들 전체를 의미한다.
Fig. 1은 수소전기차가 어떠한 하부 시스템으로 구성되는지 도식화한 것이다. 시스템 관점의 물 관리는 주로 연료공급계에서 이루어지기 때문에 본 논문에서는 수소공급계와 공기공급계에 집중하여 연구를 수행하였다. 연료공급계의 각 구성요소 부품들은 주어진 역할에 부합하도록 설계되었으며 복수의 역할을 담당하기도 한다.
수소공급계는 고압 탱크의 수소를 적절한 압력으로 변환해 주는 압력조절기(regulator), 응축수를 제거하기 위한 기액분리기(water trap), 미반응 수소를 스택에 재공급하기 위한 이젝터(ejector)로 구성된다.
공기공급계는 외부 공기를 압축하여 연료전지 스택으로 전달하는 압축기(compressor), 압축기로부터 받은 열을 식히기 위한 열교환기(intercooler), 스택으로부터 물을 회수하여 공기에 습도를 공급하는 가습기(humidifier), 필요에 따라 유량을 조절하는 방향제어밸브(3-way valve)로 구성된다.
2.2 시스템 구성
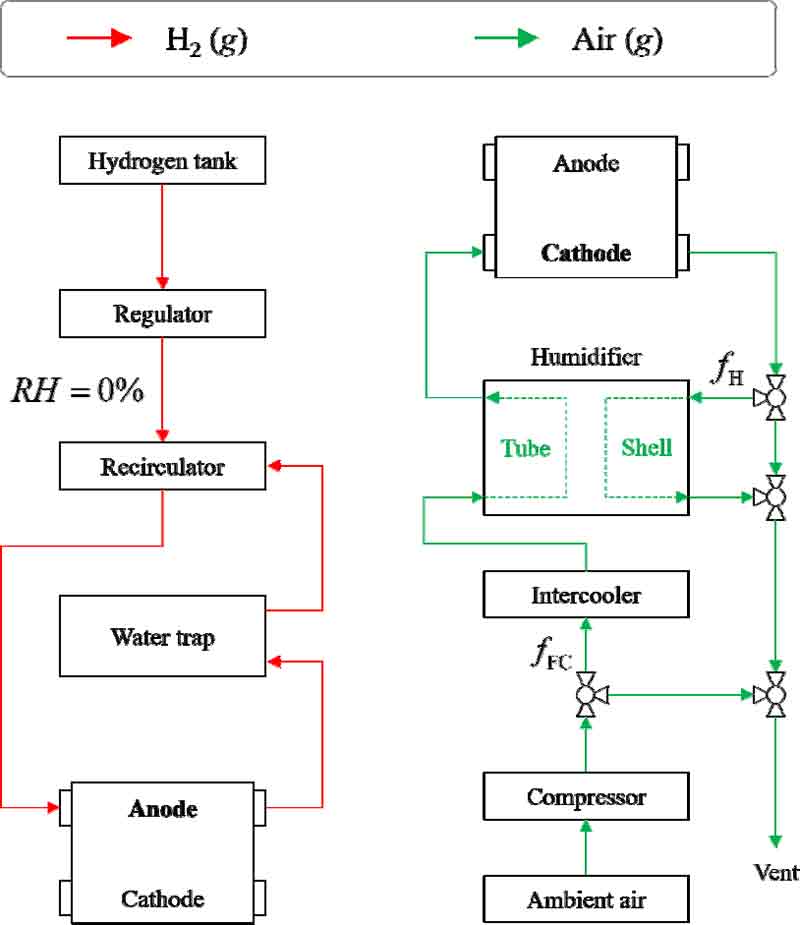
본 연구에서는 차량용 연료전지 시스템의 P&ID를 기반으로 각 구성요소 부품들을 체계적으로 분석하였다. 특히 물 관리 계통에 집중하여 연료전지 스택과 물 관리계의 주요한 구성요소 부품들을 이론적으로 모델링하고 이들을 통합하여 최적화하는 전략을 제시하였다.
Fig. 2에서 볼 수 있듯이 연료전지 시스템의 물 관리는 두 개의 구성요소 부품들의 운전으로 충족된다. 압축된 공기가 연료전지 스택에서 요구하는 유량만큼 전달되도록 조절하는 우회밸브(fFC), 연료전지 스택 공기공급계에서 발생하는 고온 습윤한 공기를 일부 배출시키거나 필요한 경우 재순환시켜 가습 과정에 활용하는 우회밸브(fH)로 구성된다.
연구의 핵심은 이러한 시스템 관점의 물 관리를 다양한 운전조건에서 시행착오를 겪는 것이 아닌, 이론적으로 예측하여 최적의 운전조건을 탐색하는 것이다. 이를 위하여 본 연구에서는 각 구성요소 부품들의 열역학적 상태를 예측하고 압축기와 밸브의 최적 운전조건을 제시하여 스택의 성능을 극대화하는 방법을 수행하였다.
3. 모델 개발
3.1 최적 운전조건 예지 전략
연료전지 시스템은 가속 환경에서 배터리가 주로 부족한 전력을 담당하고 연료전지 스택은 전력의 변화 없이 안정적으로 작동한다는 특징을 가진다. 따라서 본 연구에서는 연료전지 시스템이 정상 상태임을 가정하여 각 구성요소들을 열역학적으로 해석하였다. 먼저 연료전지 스택은 저위발열량(low heating value, LHV) 운전조건에서 연료전지 채널 출구는 항상 포화습도를 유지한다. 이를 기반으로 유사 2차원 연료전지 물 전달 모델을 개발하여 채널 입구의 요구 습도를 이론적으로 예측한다. 압축기는 연료전지 채널 입구에서 요구하는 압력에 부합하도록 작동하며 필요 이상으로 압축된 공기는 밸브를 통해 우회된다. 막 가습기는 수동적인 가습 시스템으로 공급되는 습윤 공기를 우회밸브로 조절하여 연료전지 스택의 요구 습도를 만족시킨다. 최종적으로 구성요소의 최적 운전조건과 열역학적 상태량의 변화는 연료전지 운전조건 및 외부 공기 조건에 의하여 결정된다.
3.2 연료전지 스택
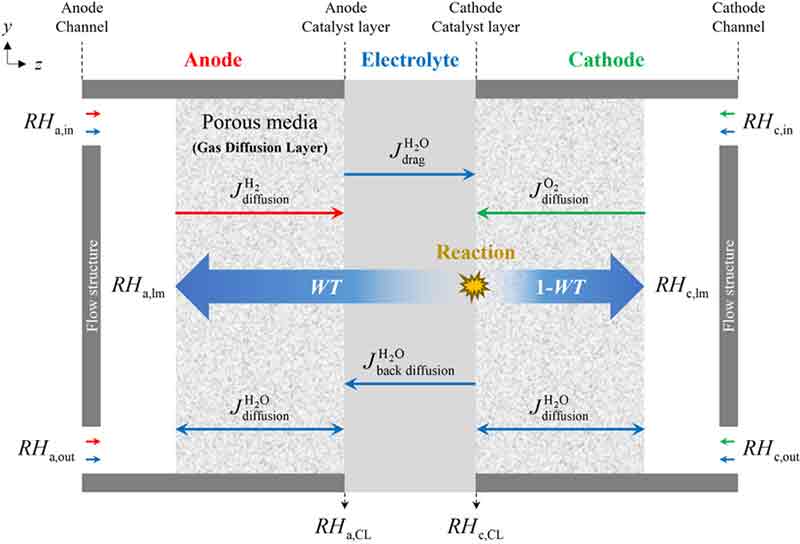
연료전지 스택은 분리판, 가스 확산층, 촉매층, 전해질 막으로 구성되며 내부에서 다양하고 복잡한 전달 현상이 발생한다. 본 연구에서는 이러한 복잡한 전달 현상을 최대한 보존하면서도 시스템 관점 해석의 용이함을 위하여 유사 2차원 모델을 개발하였다.
Fig. 3은 유사 2차원 연료전지 물 전달 모델의 개략도로 연료전지 내부의 물과 반응물의 전달 경로를 시각화하였다. 전기삼투항력(electro-osmotic drag)과 역확산(back diffusion)에 따른 물 이동을 포함하며 반응으로 생성된 물이 산화극(anode)과 환원극(cathode) 사이에서 어떻게 분포되는지 보인다. 이를 통해 연료전지 내부의 습도와 채널 입출구에서의 습도를 예측하는 데 기여한다.
LHV 운전은 연료전지에서 생성된 모든 물이 수증기 형태임을 의미하며 이로 인하여 연료전지 스택의 출구에서는 항상 포화습도를 유지하도록 설정하였다. 이는 연료전지 내 액체상의 물로 인한 전달 현상 저하를 최소화하면서 필요한 습도를 유지하여 성능을 최대화하기 위한 전략이다.
연료전지 산화극(anode)과 환원극(cathode) 채널 입구에서 각각의 요구 습도를 예측하기 위하여 각 채널로 이동하는 물의 양을 정의하였다.
| (1) |
| (2) |
총 물전달계수(net water transfer coefficient, wt)는 반응으로 인해 생성되는 물 대비 산화극(anode) 채널로 전달되는 물의 비율로 전기삼투항력과 역확산 간의 균형을 통해 연료전지에서 생성된 물이 어떻게 이동하는지 설명한다.
| (3) |
총 물전달계수가 양수일 경우 산화극 채널 쪽으로 물이 이동하는 양이 더 많음을 의미하며 음수일 경우 환원극 채널 쪽으로의 물 이동이 우세함을 나타낸다.
| (4) |
여기서 전기삼투항력()은 수소이온이 전해질 막을 통과할 때 물 분자가 이온과 함께 산화극 채널에서 환원극 채널로 이동하는 현상을 의미하며 전기삼투항력계수(ndrag)의 함수2)로 표현된다.
| (5) |
역확산은 이온전도막 내 물 함유량(λ) 차이에 의해 물 분자가 환원극 채널에서 산화극 채널로 이동하는 현상이며 이온전도막의 밀도(ρdry), 물확산계수(Dλ)로 표현2)된다.
연료전지 스택 내부의 물은 다양한 전달 메커니즘을 통해 이동한다. 먼저 촉매층(catalyst layer, CL)에서 반응이 일어나 물이 생성되면 가스 확산층(gas diffusion layer, GDL)을 지나 분리판의 각 채널(channel)까지 이동하게 되고 유동을 따라 채널 출구로 배출된다.
| (6) |
| (7) |
| (8) |
| (9) |
연료전지 CL에서 유로채널까지의 물 전달은 식 (7)과 같이 표현된다. GDL에서는 농도차에 의하여 물이 이동하는데 이는 GDL의 두께(tGDL)와 물확산계수()의 영향을 받는다. 물확산계수는 GDL의 공극률(εGDL), 온도와 압력에 관한 함수로 표현된다3). GDL과 분리판 채널 경계에서는 대류의 형태로 물이 이동하며 대류 물전달계수(hChannel)를 통해 계산된다. 대류 물전달계수는 쉐우드 수(Sh), 채널 내 물확산계수(DChannel)와 채널의 수력학적 직경(dh)에 관한 함수로 표현된다.
본 연구에서는 시스템 관점의 연료전지 스택 물 전달 해석에 필요한 경계조건을 명확하게 정의하였다. 연료전지 내 전기화학 반응은 전 면적에 걸쳐 균일하게 발생한다고 가정하였다. 또한 냉각수의 입구와 출구의 온도 차를 10℃로 설정하였다. 이는 냉각수의 열용량이 매우 크기 때문에 냉각수와 접촉하는 연료전지 채널의 입출구 온도 역시 동일하게 10℃의 차이를 유지한다고 가정하기 위함이다. 이러한 가정은 채널 내부에서 발생하는 온도 변화가 냉각 시스템에 의하여 균일하게 관리된다는 점을 반영하며 시스템 해석의 일관성을 제공한다.
3.3 막 가습기
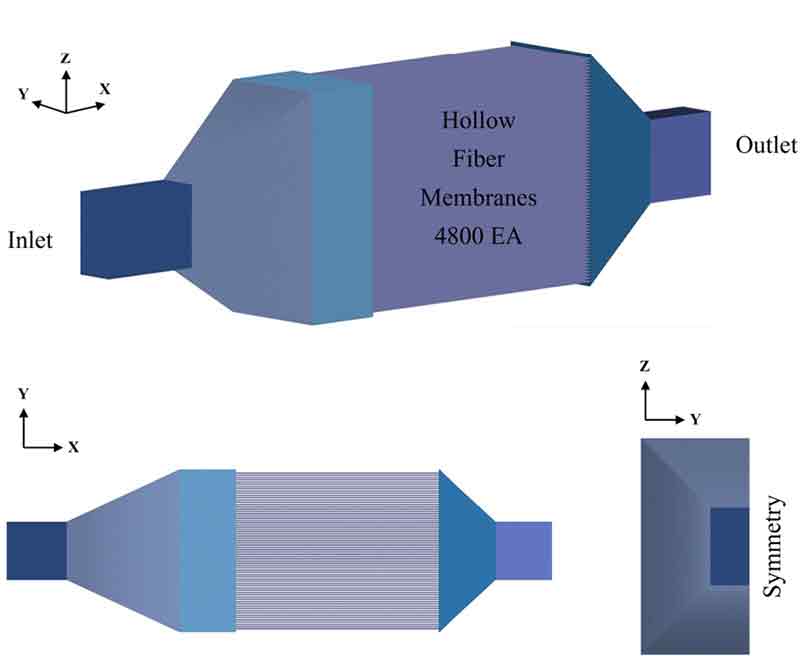
본 연구에서 사용된 막 가습기는 Fig. 4와 같이 셸 앤 튜브(shell & tube) 타입으로 가스-가스(gas-to-gas) 방식과 중공사막(hollow fiber membrane) 다발로 구성된 가습기이다. 셸 측에서는 연료전지의 환원극(cathode) 출구에서 배출된 고온 습윤한 공기가 흐르며 가습을 위한 수분을 제공한다. 튜브 측에서는 연료전지로 공급될 공기가 중공사막을 통과하며 셸 측으로부터 습도를 공급받는다. 중공사막 다발 구조는 물 전달 면적을 크게 늘려 우수한 가습 성능을 발휘한다. 이와 같은 구조를 통해 막 가습기는 연료전지 운전조건에 맞춰 적절한 습도를 유지하고 스택의 성능과 내구성을 보장하는 역할을 수행한다.
막 가습기의 가습은 농도 차에 의한 대류와 확산 방식으로 이루어진다.
| (10) |
여기서 는 막 가습기의 총 가습량을 뜻한다. 총 가습량은 물의 대수평균농도차()에 비례하며 이는 열전달 이론의 대수평균온도차(logarithmic mean temperature difference, LMTD) 개념을 모사한 것으로10) 물 전달의 구동력(driving force)을 대표한다. 또한 단위면적당 물 전달률은 가습기의 물 전달저항(RH2O)에 반비례한다.
막 가습기의 흐름 배열에 따라 대수평균농도차는 셸 측과 튜브 측 물의 입출구 농도로 표현된다. 본 모델에서는 평행류(co flow)보다 가습 성능에 유리한 대향류(counter flow) 배열이라 가정하였다.
막 가습기의 물 전달 저항은 튜브, 셸 그리고 막에서의 전달 저항으로 구분하며 전달 메커니즘에 따라 표현 가능하다.
| (11) |
여기서 hH2O는 대류 물전달계수를 의미한다. 대류 물전달계수(hH2O)는 킬턴-콜번 유사성 원리(Chilton-Colburn analogy)를 통해 계산하였다. 킬턴-콜번 유사성은 열, 물질, 운동량 전달의 기본 메커니즘에 대한 상사성을 설명하는 개념으로 본 모델에서는 대류 열전달계수(hHT)로부터 도출하였다.
| (12) |
| (13) |
여기서 루이스 수(Le)는 무차원 수로, 열확산계수(α)와 물질확산계수(D)로 표현 가능하다.
막 가습기는 연료전지 스택에 적절한 습도를 공급해주는 구성요소로 본 모델에서는 연료전지 시스템의 구성요소들과 통합적인 해석이 필요하다.
앞선 유사 2차원 연료전지 스택 모델을 통해 환원극(cathode) 채널에 요구되는 습도를 도출하였으며 이는 막 가습기 튜브 측 출구에서 충족되어야 한다. 또한 연료전지 스택 환원극(cathode) 채널 출구에서 배출되는 고온 습윤한 공기의 습도는 막 가습기의 셸 측 입구로 향하게 된다.
3.4 압축기
압축기는 임펠러(impeller)와 디퓨저(diffuser)로 구성된다. 임펠러는 공기를 고속으로 회전시켜 운동 에너지를 증가시키며 디퓨저는 공기의 운동 에너지를 압력으로 변환되도록 유도하는 역할을 한다. 임펠러와 디퓨저의 형태에 따라 다양한 종류의 압축기로 구분되며 본 연구에서는 비교적 작은 크기에도 큰 압축률을 보이는 이점을 가진 원심류형(centrifugal) 압축기를 채택하였다.
압축기 출구에서의 압력은 이상기체에 대한 등엔트로피 압축 과정의 압력과 온도 관계식으로부터 파생되어 계산된다.
| (14) |
여기서 γ는 비열비를 뜻한다. 아래첨자 Comp.는 압축기를, in과 out은 각각 입구와 출구를 의미한다. 는 실제 비 엔탈피 변화량으로 압축기의 일이 최종적으로 공기를 압축하는 데 얼마나 사용되었는지를 나타낸다.
| (15) |
여기서 은 이상적인 비 엔탈피 변화량으로 압축기의 일이 모두 공기를 압축하는 데 사용되었음을 뜻한다. 는 등엔트로피 효율을 의미하며 압축기 구동 시 발생하는 다양한 손실들을 고려하여 공기의 질량유량과 임펠러의 회전속도에 관한 관계식11)으로 계산된다.
연료전지 시스템에서 압축기의 위치는 공기를 공급하는 시작점으로 압축기 입구에서는 외부 공기가 들어와 막 가습기의 튜브 측으로 향하게 된다.
앞선 셸 앤 튜브 타입 막 가습기 모델에서 도출한 튜브 측 입구에서 요구되는 습도는 압축기 출구의 습도에서 충족되어야 한다. 또한 압축기 입구의 열역학적 상태량은 외부 공기의 상태량과 동일하다.
3.5 부가적인 구성요소 부품
본 연료전지 시스템에서는 유량을 조절하고자 2개의 우회밸브(bypass valve)를 사용한다. 하나는 연료전지 스택에서 요구하는 유량에 부합하도록 공급되는 공기의 양을 조절하고 연료전지 스택에서 요구하는 습도를 만족시키고자 막 가습기의 가습량을 조절하는 밸브이다. 본 연구에서는 앞선 주요 구성요소 부품 모델링들을 기반으로 밸브에서 각 구성요소 부품으로 향해야 하는 질량유량의 비율을 계산하였다.
본 연료전지 시스템에서는 2가지 용도의 열교환기를 사용한다. 하나는 온도를 조절하는 용(intercooler)으로 연료전지 스택에서 요구하는 온도에 부합하도록 압축기와 막 가습기 사이에서 공기의 온도를 조절한다. 해당 열교환기는 막 가습기 내부에 내장하여 사용되기도 하며 본 연구에서는 요구되는 열 교환양이 충족된다고 가정하였다. 다른 용도의 열교환기(water trap)는 습도를 조절하기 위함으로 연료전지 스택의 산화극 출구에서 배출되는 고온 습윤한 수소가 재순환이 가능하도록 온도를 조절하여 물을 액체 상태로 분리한다. 본 연구에서는 열교환기를 통해 수소의 완전한 재순환이 가능하도록 온도 및 습도 조절이 가능하다고 가정한다.
4. 결과 및 고찰
4.1 모델 검증
본 절에서는 개발한 연료전지 시스템의 주요 구성요소 부품 모델링을 검증한다.
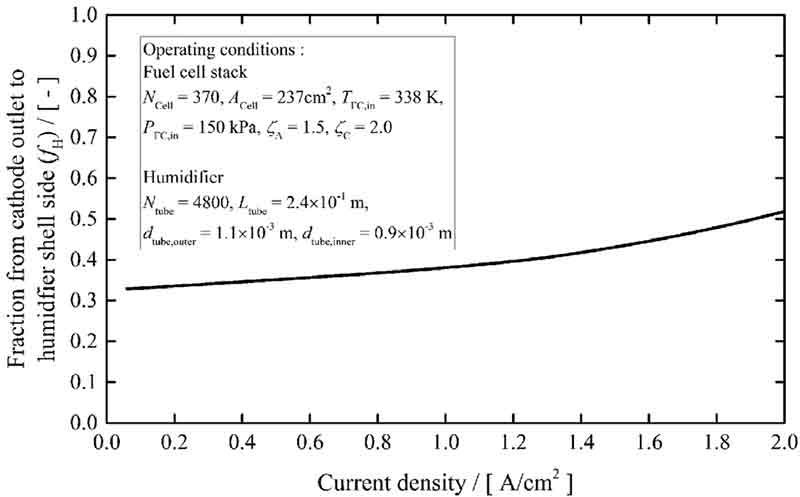
Fig. 5(a)에서는 연료전지의 총 물전달계수(WT)를 본 연구에서 개발한 모델의 값과 실험값5)을 비교하였다. 총 물전달계수 변화는 두 가지 당량비 조건에 모두 유사한 결과를 보인다. 본 연료전지 스택 모델은 채널 중 가장 습윤한 출구의 습도가 포화 상태라 가정하였기에 해당 실험5)과 같은 단일 상에서 운전되는 연료전지일수록 유사한 결과를 보인다.
Experimental validation of (a) pseudo-two dimensional fuel cell water transfer model. (b) Shell and tube type membrane humidifier model
Fig. 5(b)에서는 막 가습기 셸 측 입구 습도에 따른 총 가습량 변화를 다양한 온도조건에 대해 본 모델의 값과 실험값6)을 비교하였다. 막 가습기 모델도 마찬가지로 다양한 운전조건에 대해 실험값과 유사한 결과를 보인다.
4.2 열역학적 상태량 분포도
앞서 개발된 개별 구성요소 모델들을 통합하여 LHV 운전 연료전지 시스템의 최적 운전조건을 탐색하는 것이 가능하다. Fig. 6에서는 정상 상태라는 가정하에 연료전지 시스템을 가장 보편적인 운전조건으로 구동할 때 각 구성요소 간 연결부의 열역학적 상태량(온도, 압력, 유량, 습도)을 예측한다. 여기서 대표 운전조건(reference case)은 수소전기차 구동 시 상용 운전 프로파일을 기준으로 Table 1과 같이 가장 적합한 조건12)이 선정되었다. 연료전지 스택의 대표 운전조건에 따라 계산된 연료전지 시스템의 구성요소 부품들의 최적 운전조건은 Table 2에 정리하였다.
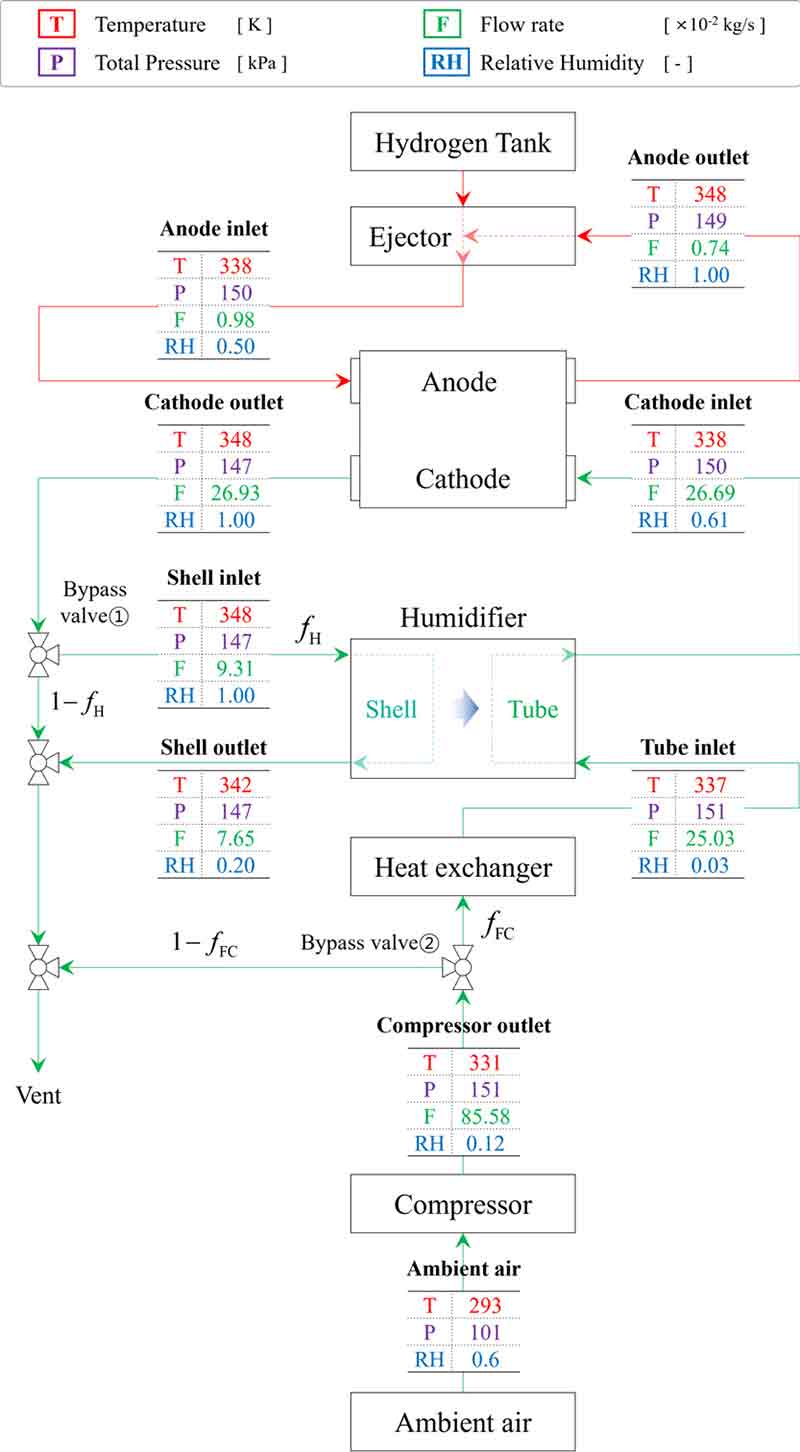
Fuel cell system thermodynamic states for a reference case based on a piping and instrumental diagram
본 연료전지 스택 물 전달 모델은 LHV 운전을 기반으로 채널 입구부에서 요구하는 습도를 이론적으로 예측한다. 대표 운전조건에 따른 연료전지 스택 채널 입구부의 요구 습도는 환원극(cathode) 채널이 산화극(anode) 채널에 비해 크며 이는 순수한 수소로 구성된 산화극 채널의 상대적으로 적은 유량 때문이다. 총 물전달계수는 반응으로 생성된 물 대비 산화극 채널로 이동한 물의 비율을 의미하며 약 9%만으로도 산화극 채널의 출구부가 충분히 포화 상태에 이르게 됨을 짐작할 수 있다. 이는 본 연료전지 스택 모델은 산화극 채널과 환원극 채널이 대향류(counter flow)의 흐름 배열이라는 특징으로 인하여 연료전지 내부의 물이 순환하게 되어 평행류(co flow)에 비해 전기삼투항력(electro-osmotic drag)보다 역확산(back diffusion)의 영향이 감소하기 때문이다.
막 가습기는 고정된 형상으로 독립적인 구성요소 부품으로써 수동적으로만 가습량이 조절된다. 따라서 우회밸브(bypass valve)를 연료전지 환원극 채널 출구부에서 막 가습기의 셸 측으로 향하는 부분에 설치하여 능동적으로 가습량을 조절하고자 하였다.
Fig. 6과 같이 연료전지 스택 대표 운전조건에서 연료전지 스택 환원극 채널 입구부의 요구 상대습도에 따라 필요 가습량과 우회밸브의 운전조건이 결정된다. 가습기 튜브 측 출구부의 상대습도가 61%에 이르게 하기 위하여 연료전지 스택의 환원극 채널 출구에서 배출되는 고온의 포화 상태인 공기 35%만 막 가습기 셸 측 입구로 향하게 된다(fH). 즉 본 막 가습기 가습량 조절 모델은 연료전지 요구 습도에 부합하도록 목표하는 양의 정확한 물 회수가 가능하다. 또한 셸 측 출구부의 습도는 20%로 비교적 작다. 이는 본 막 가습기 모델은 셸 측과 튜브 측이 대향류의 흐름 배열이라 가정하였기 때문에 셸 측의 유량이 작을수록 셸 측의 습도는 튜브 측의 습도에 가까워진다.
압축기는 성능곡선을 기반으로 연료전지 스택 요구 압력에 따라 유량이 결정된다. 하나의 압축기 출구 압력에 대한 최고 효율을 갖는 운전조건은 단 하나로 대표 운전조건에 대한 압축기 임펠러의 최적 회전속도가 도출된다. 결정된 압축기 출구의 유량은 일반적으로 연료전지 스택에서 요구하는 공기유량보다 크기 때문에 이에 부합하도록 일부 우회되어 연료전지 시스템 외부로 배출된다. 본 연료전지 시스템 물 관리 모델의 결과에 따르면 약 31%만 압축기 출구에서 연료전지로 향하게 된다. 이는 연료전지 스택의 운전 전류밀도에 비해 연료전지의 요구 압력이 높게 설정되었음을 뜻한다. 연료전지 스택의 저전력 운전 시에는 요구 유량이 적기 때문에 적은 압축기의 부하로도 관리가 가능하다.
4.3 우회밸브 최적 운전조건
압축기는 기생전력을 소비하는 구성요소이기 때문에 최대 효율 구간에서 운전할 필요가 있다. 따라서 본 연료전지 시스템 물 관리 모델에서는 압축기의 효율이 최대가 되도록 운전조건을 설정하였다. 또한 압축기는 연료전지 스택 입구의 요구 압력에 부합하도록 운전하여야 하기 때문에 성능곡선을 기반으로 압축기 출구단의 유량과 임펠러의 회전속도를 계산하였다. 이때 압축기 출구단의 유량은 일반적으로 연료전지 스택 요구량보다 크기 때문에 본 연구에서는 압축기 출구단에 우회밸브를 두어 연료전지 스택의 요구량에 부합하도록 유량을 조절하였다.
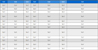
Fig. 7에서는 연료전지 스택 요구 전력에 따른 압축기와 그 출구단의 우회밸브의 최적 운전조건을 나타내었다. y축 중 좌측은 압축기 출구에서 연료전지 스택으로 향하는 유량의 비율로 0부터 1까지 변화하며 우측의 경우 압축기 임펠러의 회전속도로 0부터 100 kRPM까지의 범위를 갖는다. x축에 수직인 1점 쇄선은 운전조건이 크게 변화하는 기준이다. 실선은 압축기 출구에서 연료전지로 향하는 유량 비율로 일정하게 증가하다가 1로 수렴하게 되며 파선은 압축기 회전속도로 미세하게 상승하다가 점차 가파르게 상승한다. 연료전지 스택 입구의 요구 압력은 1.5 bara로 일정하기에 최대 효율에 따른 압축기의 출구유량은 일정하다. 따라서 압축기 출구의 유량이 연료전지 스택 요구 유량보다 크다면(1점 쇄선의 좌측 구간) 유량 비율(실선)은 일정하게 증가하고 압축기의 회전수(파선)는 유량 증가에 따른 압력 손실만을 고려하여 보정된다. 하지만 압축기 최대 효율 지점에서 연료전지 스택의 요구 유량을 충당할 수 없다면(1점 쇄선의 우측 구간) 효율을 포기하고 유량을 만족하는 전략으로 전환한다. 연료전지 스택의 요구 유량과 요구 압력을 동시에 만족하도록 압축기가 작동하기에 압축기 출구의 유량은 모두 연료전지 스택으로 향하게 된다. 또한 압축기는 효율이 감소하여 운전압력에 도달하도록 회전속도가 더 빨라지게 된다.
막 가습기는 연료전지 스택에 요구하는 습도에 부합하도록 적절하게 가습할 필요가 있다. 그러나 막 가습기는 설계된 형상과 연료전지 운전조건에 의해서만 가습량이 변화하는 수동적인 가습 시스템이다. 따라서 연료전지 환원극(cathode) 채널 출구단의 물을 회수하기 위하여 제공받는 고온 습윤한 가스의 양을 조절하여 막 가습기를 능동적인 가습 시스템으로 전환하고자 하였다.
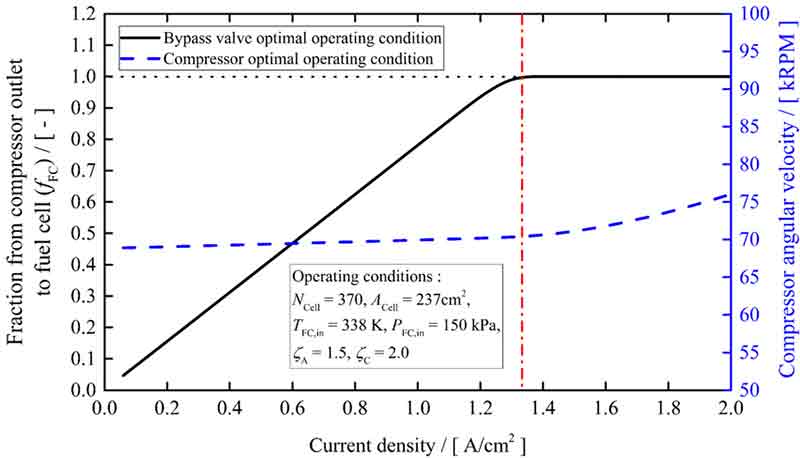
Fig. 8은 연료전지 스택의 요구 전력에 따른 연료전지 스택으로부터 막 가습기 셸 측으로 향하는 습윤한 가습의 유량 비율(fH)이다. 이는 연료전지 운전조건에 따른 막 가습기가 제공하여야 하는 가습량으로 연료전지의 요구 습도 변화를 의미한다. y축은 유량 조절 비율로 범위는 0부터 1까지이다. 만약 습윤 가스의 비율을 조절하는 우회밸브가 존재하지 않는다면 막 가습기로 향하는 가스 비율은 항상 1일 것이다. 그렇다면 연료전지 스택에서 요구하는 습도보다 더 많은 가습량으로 인하여 연료전지 채널에 응축수가 발생하여 반응물 전달 현상 저하 문제까지 이어지게 된다. Fig. 8의 x축인 연료전지의 전류밀도는 동일한 당량비 조건하에 요구하는 유량을 뜻한다. 본 연구 결과에 따르면 유량이 증가함에 따라 막 가습기로 향해야 하는 습윤한 가스의 비율(fH)은 지수함수 개형의 우상향 곡선을 그린다. 이는 고전류밀도 운전 시 연료전지에서 반응으로 생성되는 물이 많아져 역확산의 영향이 증가하고 산화극(anode) 채널로 넘어가는 물의 비율(총 물전달계수)이 상승하기 때문이다. 즉 연료전지 환원극 채널 입구의 요구 습도가 증가하여 이에 따라 막 가습기로 향하는 습윤 가스의 비율이 커지게 되는 것이다. 하지만 유량이 많아짐에 따라 물 전달 저항은 일정한 값으로 수렴하게 되어 가습량은 정비례하게 증가하지 않는다. 따라서 이를 보충하기 위해 고전류에 가까워질수록 막 가습기에 투입되는 습윤 가스의 비율(fH)을 증가시켜야 하기 때문에 지수함수의 개형을 띄게 된다.
5. 결 론
본 연구에서는 기존 피드백 형태의 시행착오적 시스템 접근에서 벗어나 LHV 가정하의 연료전지 스택으로부터 역공학적 해석이 가능한 체계적인 기틀을 마련하였다. 이를 위하여 연료전지 시스템 중 물 관리에 주요한 구성요소 부품들의 열역학적 이론 기반 모델링을 개발하였으며 실험값과 비교하여 검증을 진행하였다. 개발한 주요 물 관리 구성요소 부품 모델링들을 통합하여 차량용 연료전지 시스템을 기반으로 대표 운전조건에 따른 열역학적 상태량 분포를 예측하였다. 또한 연료전지 스택의 전류밀도에 따른 능동적 구성요소들(압축기, 우회밸브)의 최적 운전조건을 도출하였다. 본 연구에서는 구성요소 간의 상호작용이 손실 없이 이루어진다고 가정하였으나 실제 연료전지 시스템은 구성요소 간 연결부에서 열 및 물질 등의 손실이 발생하기 때문에 향후 해당 부분을 고려해야 할 필요가 있다.
- 1) LHV 가정하에서 연료전지 스택의 역공학적 이론 기반 접근법을 도입하여 시스템 구성요소들의 최적 운전조건이 예측 가능한 개념을 적립하였다.
- 2) 차량용 연료전지 시스템의 대표 운전조건에 따른 전체 열역학적 상태량(온도, 압력, 유량, 습도) 분포도를 제공함으로써 시스템 전반의 열 및 물질의 흐름을 예측할 수 있는 환경을 마련하였다.
- 3) 압축기 출구단에 우회밸브를 설치함으로써 다양한 운전조건에서 연료전지 스택이 요구하는 압력과 유량을 만족하도록 하였으며 동시에 압축기의 고효율 운전을 고려하여 최적의 운전조건을 탐색하였다.
- 4) 연료전지 스택의 요구 유량은 전류밀도에 따라 변화하기 때문에 압축기의 기생전력을 최소화하기 위해서는 저전류 구간에서는 저압운전이, 고전류 구간에서는 고압운전이 유리하다.
- 5) 막 가습기 셸 측 입구단에 우회밸브를 설치함으로써 가습량을 능동적으로 조절하고 연료전지 스택에서 발생할 수 있는 지나치게 건조하거나 습윤한 환경을 통제하여 스택의 내구성을 보장할 수 있다.
Nomenclature
| A : | Area (m2). |
| H2O : | Water. |
| C : | Molar concentration (mol/m3). |
| 0 : | Reference conditions. |
| cp : | Heat capacity (J/kg·K). |
| Channel : | Gas flow channel. |
| D : | Diffusion coefficient (m2/s). |
| CL : | Catalyst layer. |
| d : | Diameter (m). |
| Comp. : | Compressor. |
| F : | Faraday constant (C/mol). |
| GDL : | Gas diffusion layer. |
| h : | Convective transfer coefficient (m/s). |
| h : | Hydraulic. |
| : | Enthalpy (J/kg). |
| Humi. : | Humidifier. |
| i : | Current density (A/cm2). |
| in : | Channel inlet. |
| J : | Molar flux (mol/m2·s). |
| lm : | Logarithmic mean. |
| Le : | Lewis number. |
| m : | Membrane phase. |
| M : | Equivalent molecular weight (g/mol). |
| Osmotic drag : | Electro-osmotic drag. |
| : | Mass flow rate (kg/s). |
| out : | Channel outlet. |
| ndrag : | Electro-osmotic drag coefficient. |
| real : | Real case. |
| P : | Pressure (Pa). |
| Sh : | Sherwood number. |
| T : | Temperature (K). |
| t : | Thickness (m). |
| U : | Rotational speed of compressor (RPM). |
| WT : | Net water transfer coefficient. |
| α : | Thermal diffusion coefficient (m2/s). |
| γ : | Ratio of specific heat. |
| ε : | Porosity. |
| λ : | Membrane water content (H2O/SO3-). |
| ρ : | Density (kg/m3). |
| eff : | Effective. |
Acknowledgments
본 연구는 신재생에너지핵심기술사업인 민군 공동 활용을 위한 정격 100 kW급 이동형 수소연료 발전기 및 확장식 수소 공급장치 개발(RS-2024-00424428) 과제와 물 흐름 제어를 통한 PEMFC 성능 및 내구성 2배 이상 향상을 위한 혁신 기술 개발(20223030030110) 과제와 수소차용차세대연료전지시스템기술개발사업인 연료전지시스템 효율 향상을 위한 단위 셀 핵심기술 개발(1415186266 [20012133]) 과제의 일환으로 수행되었습니다.
References
-
D. Ahn, H. Lee, H. Shim, and D. Kim, “Optimization of condensate water drain logic depending on the characteristics of drain valve in FPS of fuel cell vehicle and development of anode water management strategy to achieve high fuel efficiency and operational stability”, Journal of Hydrogen and New Energy, Vol. 27, No. 2, 2016, pp. 155-162.
[https://doi.org/10.7316/KHNES.2016.27.2.155]

-
T. E. Springer, T. A. Zawodzinski and S. Gottesfeld, “Polymer electrolyte fuel cell model”, Journal of The Electrochemical Society, Vol. 138, No. 8, 1991, pp. 2334-2342.
[https://doi.org/10.1149/1.2085971]

-
S. Um, C. Y. Wang, and K. S. Chen, “Computational fluid dynamics modeling of proton exchange membrane fuel cells”, Journal of The Electrochemical Society, Vol. 147, No. 12, 2000, pp. 4485-4493.
[https://doi.org/10.1149/1.1394090]

-
S. Park, M. H. Kim, and S. Um, “Phase separation modeling of water transport in polymer electrolyte membrane fuel cells using the multiple-relaxation-time lattice Boltzmann method”, Chemical Engineering Journal, Vol. 495, 2024, pp. 153629.
[https://doi.org/10.1016/j.cej.2024.153629]

-
H. Ito, T. Mimoto, S. Someya, and T. Munakata, “Net water drag coefficient during high temperature operation of polymer electrolyte fuel cells”, Journal of The Electrochemical Society, Vol. 168, No. 12, 2021, pp. 124505.
[https://doi.org/10.1149/1945-7111/ac3b08]

-
H. N. Vu, X. L. Nguyen, J. Han, and S. Yu, “A study on vapor transport characteristics in hollow-fiber membrane humidifier with empirical mass transfer coefficient”, International Journal of Heat and Mass Transfer, Vol. 177, 2021, pp. 121549.
[https://doi.org/10.1016/j.ijheatmasstransfer.2021.121549]

-
D. Cho and H. S. Kim, “A study of the effect of compressor performance map on the efficiency of high-pressure operating PEMFC systems in automotive applications”, Journal of Hydrogen and New Energy, Vol. 23, No. 6, 2012, pp. 604-611.
[https://doi.org/10.7316/KHNES.2012.23.6.604]

-
D. Seok, M. Kim, Y. J. Sohn, and J. Lee, “Operational optimization of anodic/cathodic utilization for a residential power generation system to improve system power efficiency”, Journal of Hydrogen and New Energy, Vol. 24, No. 5, 2013, pp. 373-385.
[https://doi.org/10.7316/KHNES.2013.24.5.373]

-
B. K. Hong and S. H. Kim, “Recent advances in fuel cell electric vehicle technologies of Hyundai”, ECS Transactions, Vol. 86, No. 13, 2018, pp. 3-11.
[https://doi.org/10.1149/08613.0003ecst]

- Y. A. Cengel, “Heat transfer: a practical approach”, 2nd ed, McGraw-Hill, USA, 2002.
-
J. T. Gravdahl, F. Willems, B. de Jager, and O. Egeland, “Modeling of surge in free-spool centrifugal compressors: experimental validation”, Journal of Propulsion and Power, Vol. 20, No. 5, 2004, pp. 849-857.
[https://doi.org/10.2514/1.10052]

-
H. Lohse-Busch, M. Duoba, K. Stutenberg, S. Iliev, M. Kern, B. Richards, M. Christenson, and A. Loiselle-Lapointe, “Technology assessment of a fuel cell vehicle: 2017 Toyota Mirai”, Argonne National Laboratory Energy Systems Division, USA. Retrieved from https://publications.anl.gov/anlpubs/2018/06/144774.pdf, .
[https://doi.org/10.2172/1463251]