PEMFC 유로 형상과 유입 유량 변화에 따른 차압 성능 및 균일 지수 분석
2024 The Korean Hydrogen and New Energy Society. All rights reserved.
Abstract
This study aims to provide fundamental data to improve proton exchange membrane fuel cell (PEMFC) performance. A physical model of the bipolar plate was reverse engineered by 3D scanning, and straight, micro-mesh, and wavy channels were analyzed. Differential pressure, internal flow characteristics, and uniformity index were evaluated under various inlet flow rates. The results show that increased inlet flow rates raised pressure and velocity, while wavy and baffled channels disturbed flow uniformity and resultsd in uneven distribution. In contrast, micro-mesh and converging-diverging straight channels promoted uniform flow and reduced pressure drop. Therefore, straight and micro-mesh channels are recommended for optimized PEMFC performance.
Keywords:
Bipolar plate, Differential pressure, PEMFC, Spatial average, Uniformity index키워드:
분리판, 차압, 고분자 전해질 연료전지, 공간적 평균값, 균일 지수1. 서 론
화석연료는 오랜 기간 주요 에너지원으로 사용되어 왔으나 환경오염과 자원 고갈 및 기상이변 등의 여러 가지 문제로 인하여 새로운 친환경 대체 에너지원이 필요하게 되었다. 이러한 배경에서 수소는 부산물이 물(H2O)뿐이라는 점에서 화석연료와 달리 친환경적인 에너지 자원으로 평가받고 있다. 특히 수소를 주요 연료로 활용하는 발전 장치 중 연료전지(fuel cell)는 효율적인 에너지원으로 주목받고 있다1).
일반적으로 연료전지는 전해질 유형 및 작동 조건에 따라 분류된다. 그중 proton exchange membrane fuel cell (PEMFC)은 수소를 연료로 사용하여 전기를 생산하는 장치로 수소(H2)와 산소(O2)의 전기화학적(electrochemical) 반응을 통해 전력을 생성하면서 물 외에 유해한 배출물이 없다는 점에서 친환경 에너지원으로 평가받고 있다2).
이외에도 PEMFC는 다양한 이점들을 가지고 있다. 첫째, 높은 에너지 효율이다. 이는 기존 내연기관에 비해 더 적은 에너지 손실을 유발한다. 둘째, 운전 중에 발생하는 온실가스인 NOx와 SOx의 배출이 없어 탄소 중립 목표를 달성하는 데 중요한 역할을 한다. 셋째, 신속한 시동과 100℃ 이하의 낮은 온도에서의 운전이 가능하여 수송용 에너지원으로도 적합하다2,3).
PEMFC의 분리판(bipolar plates)은 연료와 산화제를 각각 양극과 음극으로 분배하는 중요한 역할을 하며 PEMFC 내부의 전기화학 반응에 필요한 유로를 형성한다. 또한 분리판 내부의 차압 성능은 연료전지 시스템 내에서 기체 흐름 및 배출과 반응 효율성을 조절하여 성능 저하와 기체 공급 부족 현상을 방지하는 인자이며 균일지수(uniformity index)는 반응 물질 분포의 균일성을 측정하는 지표로 연료전지의 성능과 효율을 나타내는 중요한 요소이다. 분리판의 설계는 전기적 전도도와 반응물 전달의 효율성을 최적화하는 데 중점을 두며 이를 위해 다양한 유로(flow field) 설계 대상으로 실험 및 수치해석 연구가 진행되고 있다.
Ahn 등4)은 높은 온도 조건의 양성자 교환막 연료전지(high temperature PEMFC, HT-PEMFC)에서 분리판의 사문형 유로와 직선형 유로의 성능 비교를 위해 수치해석을 진행하였다. 직선형 유로의 경우 유량 편차를 최소화하기 때문에 HT-PEMFC에는 직선형 유로의 사용이 유리하다는 점을 강조하였다. Lee 등5)은 유로 폭 비율을 서로 다른 세 가지 유로 형상에 적용하여 수치해석을 진행하였다. 물 관리 성능을 비교 분석한 결과에 따르면 유로 폭을 줄이는 것이 외부로 배출되는 물의 양을 줄이는 것이 확인되었다. 또한 건조한 상태에서 시동 시 연료전지의 탈수 현상을 억제할 수 있다는 사실을 입증하였다. Jung6)은 분리판의 직렬형과 병렬형 유로의 성능 파악을 위하여 분리판 내 균일한 유동 분포를 평가하였고 최적의 유로 형상을 선정하여 실험에 적용하였다. 그 결과 직렬형 분리판의 성능이 우수하며 압력 강하가 큰 순서대로 물질의 반응이 활발하다는 것7)을 확인하였다. Hwang 등8)은 미세한 금속 메시 유로 형상을 사문석 유로 형상과 비교하기 위하여 수치해석을 진행하였다. 이를 통해 gas diffusion layer를 통한 triple boundary base로 우수한 기체의 확산 성능, 물 배출, 전력 출력이 증가함을 보였다.
선행 연구를 종합해 보면 특정 유로 형상이 연료전지의 차압 성능과 반응 물질의 균일 분포에 영향을 미치는 것으로 판단된다. 이러한 연구들은 유로 설계가 연료전지 내에서 흐름 균일성과 성능에 어떤 영향을 미치는지 규명하고 다양한 유로 설계를 비교하여 최적의 구조를 제안하고 있다. 그러나 수치해석 및 실험에 사용된 분리판은 단순한 구조로 연구를 위해 자체 제작되었으며 연료와 산화제의 유입 유량이 차압 성능과 반응 물질의 균일한 분포에 미치는 영향을 고려한 연구는 부족하다. 특히 실제 상용화된 PEMFC 분리판을 기반으로 한 연구는 상대적으로 드물다9). 따라서 다양한 유로 형상과 유입 조건이 결합된 수치해석 연구가 필요하다.
본 연구에서는 고효율과 저차압 특성을 가지는 새로운 PEMFC 분리판 제작을 위해서 현재 수송 분야에서 출력 성능과 효율이 가장 뛰어난 PEMFC의 두 가지 분리판을 대상으로 3D 스캐닝 기법을 통해 역설계한 후 전산 모델로 변환하고 유로 형상과 유입 유량 변화에 따른 속도, 차압 성능 및 균일 지수와 같은 유동 특성을 분석하였다. 이를 바탕으로 연료전지 성능 향상을 위한 기초 데이터를 확보하는 것을 목표로 하였다.
2. 연구 방법
2.1 수치해석 대상 및 설계
본 연구에서 type A와 B의 두 분리판을 대상으로 3D 스캐닝 기법 중 레이저 스캐닝(laser scanning)을 활용하였다. 실물 분리판의 반사된 빛을 측정하여 분리판의 3D 좌표를 생성하였고 CATIA 소프트웨어(Dassault Systèmes, Vélizy-Villacoublay, France)를 통해 좌표를 CAD 상태의 기하학적 모델로 변환하였다. 그다음 역설계한 분리판 형상에서 내부 유체 영역을 추출하여 ANSYS Fluent (Ansys, Canonsburg, PA, USA)에 적용하였다. 이를 바탕으로 Fig. 1(a)와 Fig. 1(d)는 두 유체 영역을 겹쳐진 형상으로 나타내었고 Fig. 1(b), (c), (e), (f)는 각 분리판을 겹치기 전 연료인 수소와 산화제인 산소가 흐르는 내부 유로를 나타내었다. 또한 수소와 산소는 서로 반대로 흐르는 조건을 지정하여 기준 모델로 선정하였다.
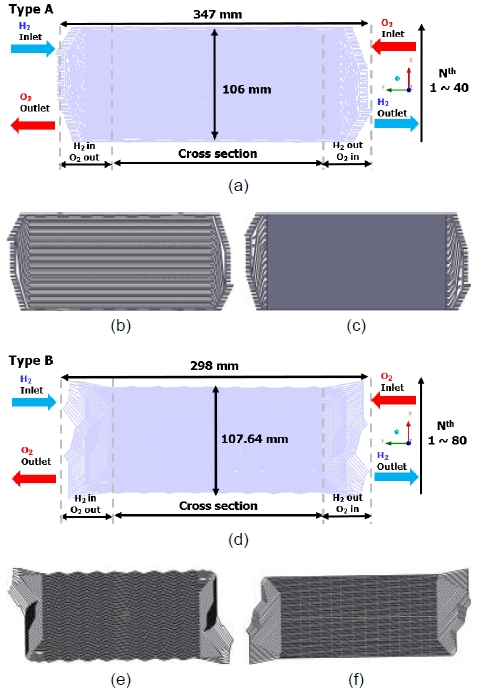
The digital reconstruction of bipolar plates. (a) Schematics of biplar plates type A for H2 and O2 flow area analysis. (b) H2 fluid domain of type A. (c) O2 fluid domain of type A. (d) Schematics of biplar plates type B for H2 and O2 flow area analysis. (e) H2 fluid domain of type B. (f) O2 fluid domain of type B.
Fig. 2는 각 분리판 내 유로 형상을 나타내었다. 수소 유로 분리판의 경우 Fig. 2(a)는 type A의 직선과 장공형 베플(straight and baffle) 유로이며 Fig. 2(b)는 type B의 사문형 물결(serpentine wavy) 유로로 확인하였다. 산소 유로 분리판의 경우 연료전지 전체의 반응률을 고려하여 Fig. 2(c)는 type A의 미세한 금속 망사(micro-mesh) 유로, Fig. 2(d)는 type B의 확관 및 축관이 배열된 직선형(converging-diverging straight) 유로로 선정하였다. 본 연구에서는 미세한 금속 망사 유로를 구현하기 위하여 직육면체 모델에 porous zone을 접목하였다.
2.2 층류 유동 모델
본 연구에서는 PEMFC 분리판 내 유동 해석을 위해 층류(laminar) 유동 모델을 적용하였다. 층류 유동은 점성이 높은 유체, 미세관 유로 경로, 짧은 유동 길이, 낮은 Reynolds 수 등에 의해 결정된다. 각 분리판은 내부의 좁은 유동 경로9,10)를 가지며 Reynolds equation을 통해 type A의 경우 13.3, type B의 경우 5.5로 낮은 Reynolds 수를 보이기 때문에 층류 유동 조건으로 진행하였다.
| (1) |
| (2) |
층류 유동 모델 선정 시 식 (1)과 같은 연속 방정식과 식 (3)과 같은 Navier-Stokes의 운동량 방정식을 적용하였으며 반응 가스는 이상기체, 정상 상태, 비압축성, 등온 조건을 가정하여 해석을 진행하였다.
| (3) |
| (4) |
위의 식에서 ρ는 밀도, t는 시간, ▽는 벡터 미분 연산, 는 속도 벡터, Sm은 질량 생성 항, P는 정압, 는 응력 텐서를 의미하고 식 (4)를 통해 도출된다. I는 단위 텐서를 의미하며 비압축성 유체의 경우 밀도가 일정해져 식 (2)와 같은 연속 방정식을 나타낸다.
2.3 수치해석 조건
유입 유량 변화에 따른 두 분리판에서의 차압, 속도, 균일 지수를 비교 분석하기 위하여 작동 유체는 수소와 산소로 하였고 유입 유량은 각 분리판 제조사의 조건을 참고하여 반응 면적 비율로 나누었다. Type A는 수소 유로에서 0.56-2.82 LPM, 산소 유로에서 1.79-8.96 LPM을 적용하였고 type B는 수소 유로에서 0.63-3.14 LPM, 산소 유로에서 1.99-9.95 LPM으로 적용하였다. 각 유로 면에 5개의 유입 유량은 Table 1에 자세히 나타내었다11,12).
PEMFC는 압력 증가 시 분리판 내 유로에서 촉매 층으로 확산이 일어난다. 따라서 작동 압력에서 분리판 내 균일한 유동을 형성하기 위하여 분리판 입구에서 1.5 atm과 출구에서 1 atm 압력 조건을 적용하였다. 또한 수소와 산소의 입구와 출구 온도 조건으로는 PEMFC의 전기화학 반응에 의한 열화를 방지하기 위한 65℃의 온도 조건을 적용하였다13,14).
Fig. 3에 두 분리판의 유입 유량에 따른 유동 특성 분석을 위한 측정 위치에 대하여 나타내었다. 두 분리판은 수소와 산소의 유동에 따라 위치에서 달라지는 압력과 속도를 평가하고자 분리판의 중심축인 plane 3을 기준으로 양옆으로 40 mm의 동일한 간격으로 plane을 설치하였다. 식 (6)은 위의 측정 위치에서 분리판 유로 내 수소와 산소 질량 유량의 균일한 분포를 정량적으로 나타내기 위하여 활용한 균일지수 방정식을 나타낸 것이다.
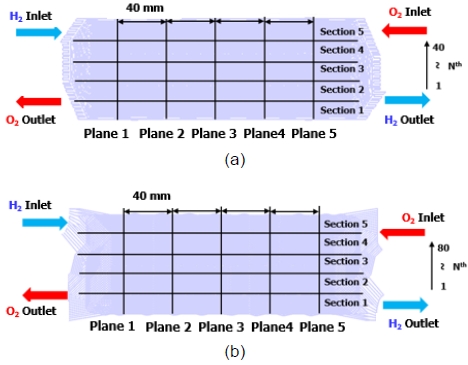
Measurement position of all condition. (a) Measurement position of type A. (b) Measurement position of type B.
균일지수는 연료전지 시스템에서 전극이나 가스 흐름의 균일성을 평가하는 중요한 지표로 사용된다. 연료전지는 성능 향상을 위해 반응 유로와 맞닿는 면적에서 전기화학 반응이 고르게 발생하여야 한다. 이를 위해서 반응 물질이 유로 전체 면적에 고르게 분포할 수 있어야 하며 전지 해석을 진행하지 않았기 때문에 간접적으로 반응 물질의 분포 정도를 파악하기 위해서 균일 지수를 활용하였다.
여기서 N은 유로의 수를 뜻하며 type A는 40개의 유로를, type B는 80개의 유로를 포함한다. 는 i번 유로의 질량 유량, 는 평균 질량 유량을 나타내며 균일지수 값이 0에 가까울수록 균일한 값을 의미한다.
Table 2는 Fig. 3과 같이 section의 기준을 나타냈다. 동일한 공간 면적을 지정하여 공간 면적 내에서 압력, 속도의 결과를 비교하기 위해서 type A는 8개, type B는 16개로 평균값을 산출하여 5개의 section으로 나누었다.
2.4 격자 의존성 검증
Fig. 4는 수치해석 결과의 신뢰성을 확보하기 위하여 격자 의존성 검증의 진행 결과를 나타낸 것이고 Table 3에는 격자 형상에 따른 해석 결과를 비교하기 위하여 격자의 크기를 감소시키며 mesh size 1-5에 대한 격자의 수를 표기하였다.
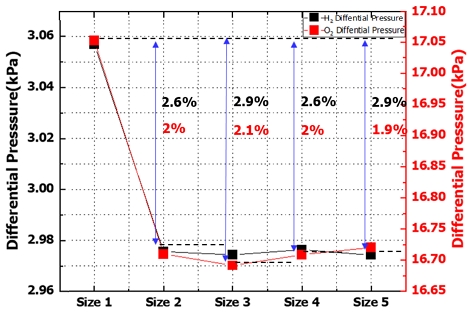
Maharudrayya 등15)은 사형 유로 형상을 통한 결과를 나타내기 이전에 격자의 크기에 따른 차압을 평가하였다. 차압 성능은 PEMFC 내에서 유입 유량의 균일한 분배와 전기화학 반응 후 생성되는 물의 배출에 영향을 미친다. 차압이 커질수록 반응물의 확산 성능이 상승하나 시스템 내부에 과도한 반응으로 만들어진 응축수가 flooding 현상을 발생시켜 성능을 저하시킨다. 차압이 낮아질수록 전지 내부로 반응 물질을 공급하는 펌프와 같은 보조 장치의 에너지 소비를 줄이고 반응 물질의 흐름을 균일하게 만든다. 본 연구의 목적은 전지의 출력 성능이 아닌, 분리판 유로 형상에서의 유동 특성을 파악하는 것이기 때문에 PEMFC 분리판 내의 유동에는 낮은 차압이 형성되는 것이 균일한 유동에 이점이 있다고 판단하여 격자 의존성 검증에 인자로 분리판 내 입구와 출구의 차압을 선정하여 비교 분석을 진행하였다.
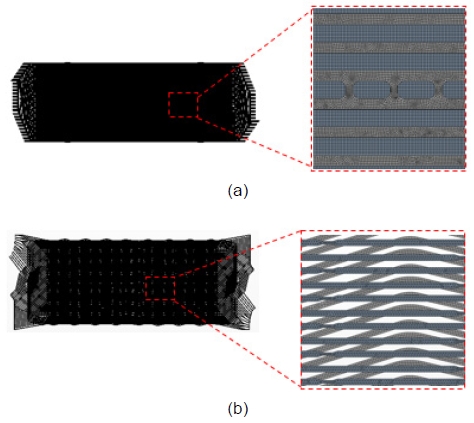
해석 결과 수소와 산소 유로에서 mesh size 1을 기준으로 mesh size 2의 경우 2.6%와 2.0%의 오차를 보였다. 이는 격자 수가 해석 결과의 정확도에 영향을 미치는 것으로 판단하였다. 또한 mesh size 3의 경우 2.9%와 2.1%, mesh size 4의 경우 2.6%와 2.0%, mesh size 5를 비교할 경우 2.9%와 1.9%의 결과 오차를 보였다. 해석 값의 정확도를 고려하여 보면 mesh size 2-4의 결과가 균일한 차이를 보였다. 그중 mesh size 2와 4의 산소와 수소 유로에서 차압 결과가 0.6%로 적은 차이를 보였다. 격자의 조밀성과 해석 시간 절약을 고려하였을 때 mesh size 4가 정확한 결과를 보일 것으로 판단되어 mesh size 4 조건을 이후 해석 과정에 적용하였다. Fig. 5는 mesh size 4 조건을 이용한 두 분리판 유로에 생성된 격자를 나타내었다. 좁은 유로 유동 해석을 위해서 정사면체와 정육면체, 프리즘 격자가 적절히 조합되도록 설정하였으며 격자의 수는 10,909,105개로 형성되었다.
3. 결과 및 고찰
3.1 유입 유량에 따른 type A의 압력 및 속도 결과 분석
Fig. 6(a), (c)는 유입 유량 변화에 따른 type A의 수소 영역과 산소 영역에서 압력 분포를 나타내었으며 case 1-5는 Table 1과 같이 분리판 type별 유입 유량 조건을 의미한다. Fig. 6(b), (d)는 최대 유입 유량 조건인 case 5일 때 Fig. 3의 측정 위치에서 압력 결과를 나타낸 그래프이다. Fig. 6(e), (g)는 속도 분포를 나타내며 Fig. 6(f), (h)는 case 5 조건에서 속도 결과를 나타내었다.
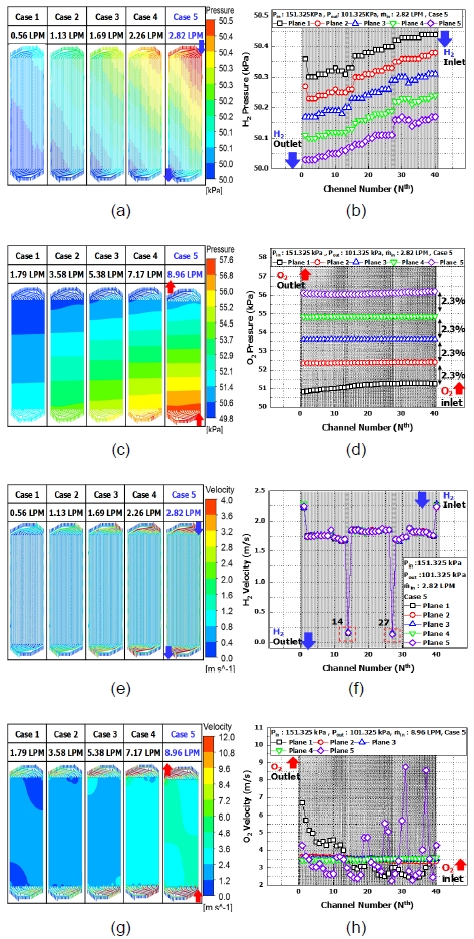
Pressure and velocity contour of type a with increase mass flow rate in all condition. (a) H2 pressure contour of type A. (b) H2 pressure distributions. (c) O2 pressure contour of type A. (d) O2 pressure distributions. (e) H2 velocity contour of type A. (f) H2 velocity distributions. (g) O2 velocity contour of type A. (h) O2 velocity distributions.
모든 조건에서 분포도 결과로 case 1에서 case 5까지 유입 유량의 증가는 압력과 속도가 상승하는 인자로 판단되며 수소 유로 영역인 Fig. 6(b), (f)의 경우 압력이 plane 1에서 최대 50.44 kPa, plane 5에서 최소 50.03 kPa가 나타나 유로 내부 차압(ΔP)은 0.41 kPa이 발생하였다. 유속은 plane 1에서 plane 5까지 과정 동안 균일하게 유지되었다. 또한 14, 27번 유로에서 최소 유속 0.16 m/s가 발생하였다. 이는 Fig. 7(a)와 같이 장공형의 베플이 유동의 방향을 바꾸고 흐름의 저항을 만들어 유속이 감소하는 결과가 도출된 것으로 판단하였다.
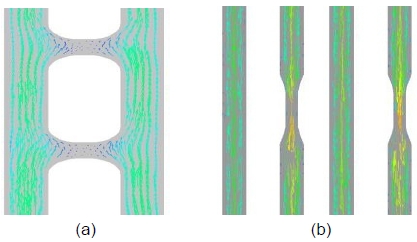
Velocity vector contour in each bipolar plates. (a) Elongated hole baffle H2 channel in type A. (b) Converging-diverging O2 channel in type B.
산소가 흐르는 Fig. 6(d), (h)의 미세 공극 유로의 경우 plane 5에서 최대 56.19 kPa, plane 1에서 최소 50.84 kPa가 발생하여 내부 차압(ΔP)은 5.35 kPa임을 확인하였다. 각 plane 사이의 압력 차이는 2.3%로 균일하게 나타나며 이는 미세 망사 구조를 구현하기 위하여 선택한 porous 모델의 공극이 압력을 균일하게 하는 것으로 판단하였다. 또한 산소 유로 측 내부 압력이 수소 유로의 내부 압력보다 13배 높은 차이를 보였다. 유속은 plane 5에서 최대 8.6 m/s, plane 1에서 최소 2.4 m/s가 발생하였으며 plane 2, 3, 4는 일정한 속도를 나타내었다.
수소와 산소가 배출되는 모든 영역에서 압력은 낮으면서 속도가 빨라지는 분포도를 보였다. 이는 배출되는 유로 수가 40개에서 7개로 줄어들 때 유로 전체 단면적의 감소가 일어나고 식 (1)의 질량 보존 법칙에 따라 유속이 증가하며 노즐 효과가 발생하기 때문인 것으로 보인다. 반대인 입구 영역의 경우 유로가 7개에서 40개로 증가하며 단면적이 증가하였기 때문에 유속이 느려지는 디퓨저 효과가 발생하였다.
3.2 유입 유량에 따른 type B의 압력 및 유속 결과 분석
Fig. 8은 type B의 물결 유로와 확관과 축관이 나타나는 직선형 유로에서 수소와 산소를 흘려주었을 때 유로 내부에서 압력과 유속 결과를 나타내었다. Fig. 8(a), (c)는 모든 유입 조건에서의 압력 분포를 나타내며 Fig. 8(b), (d)는 유입 유량이 case 5 조건에서 압력 결과를 그래프로 나타내었다. Fig. 8(e), (f)는 모든 유입 조건에서 유속 분포를 나타내며 Fig. 8(g), (h)는 유입 유량이 case 5 조건일 때 plane 1과 plane 5 사이의 유속 결과를 그래프로 나타내었다.
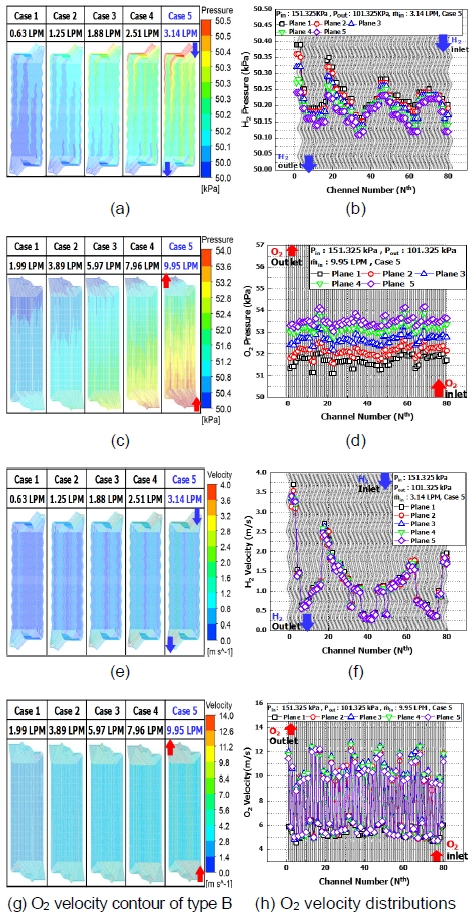
Pressure and velocity results of type B with increase mass flow rate in all condition. (a) H2 pressure contour of type B. (b) H2 pressure distributions. (c) O2 pressure contour of type B. (d) O2 pressure distributions. (e) H2 velocity contour of type B. (f) H2 velocity distributions. (g) O2 velocity contour of type B. (h) O2 velocity distributions.
유입 유량의 증가는 압력과 유속 증가의 영향을 미치는 것을 분포도를 통해 확인하였다. 수소가 흐르는 사문형 물결 유로 Fig. 8(b)의 경우 plane 1에서 최대 50.39 kPa, plane 5에서 최소 50.12 kPa이 나타나며 내부 차압(ΔP)은 0.27 kPa이 발생하였다. Fig. 8(f)에서 유속은 plane 1에서 최대 3.7 m/s로 나타났다. 이는 유입 유량이 각 유로로 분배되기 이전에 x축 방향으로 유동이 일어났고, 이로 인하여 분리판의 좌측으로 유체의 흐름이 집중되었기 때문에 높은 압력과 속도가 발생하는 것으로 파악하였다16).
산소가 흐르는 확관과 축관 형상의 직선형 유로 Fig. 8(d)의 경우 plane 5에서 최대 54.18 kPa, plane 1에서 최소 51.14 kPa이 나타나며 내부 차압(ΔP)은 3.04 kPa이 발생하였다. 물결 유로의 차압과 비교 시 11배 더 높은 내부 차압을 보였다. 또한 Fig. 8(h)에서 유속은 홀수 유로에서 최대 평균 유속이 10 m/s, 짝수 유로에서 최소 평균이 유속이 5 m/s로 나타났다. 이는 Fig. 7(b)와 같이 type B 분리판의 산소 측 유로에서 확관과 축관 형상의 반복적인 배열이 유체 흐름에 정체와 가속을 발생시켜 산소의 분포를 균일하게 만든 것으로 판단하였다.
또한 Fig. 6(b), (d)와 Fig. 8(b), (d)에서의 압력 결과를 비교하였을 때 B 분리판이 A 분리판보다 산소와 수소 유로 영역에서 더 낮은 차압 성능을 보여주었다. 이는 연료전지 분리판 내로 반응 물질을 투입할 때 펌프에서 필요한 에너지가 훨씬 적게 사용된다는 것을 의미한다17,18).
3.3 유로 형상에 따른 압력 및 유속 비교 분석
두 분리판에서 각 반응 물질 유입 유량은 상이하다19). 분리판의 유로 형상에 따른 압력과 유속을 비교 분석하기 위해서 Table 2와 같이 동일한 공간 면적을 형성하였다. 공간 면적은 두 분리판의 전체 유로 수를 기준으로 type A는 8개, type B는 16개씩으로 나누어 5개의 section 내 공간 평균값(spatial average)을 도출하여 비교를 진행하였다. Fig. 9(a), (c)는 각 section에서 수소가 흐르는 직선형 유로와 물결 유로 사이의 압력과 속도 분포를 비교한 그래프를 제시하였다. Fig. 9(b), (d)는 산소가 흐르는 미세 공극 유로와 확관과 축관이 있는 직선형 유로 사이의 압력과 유속을 비교 분석하였다.
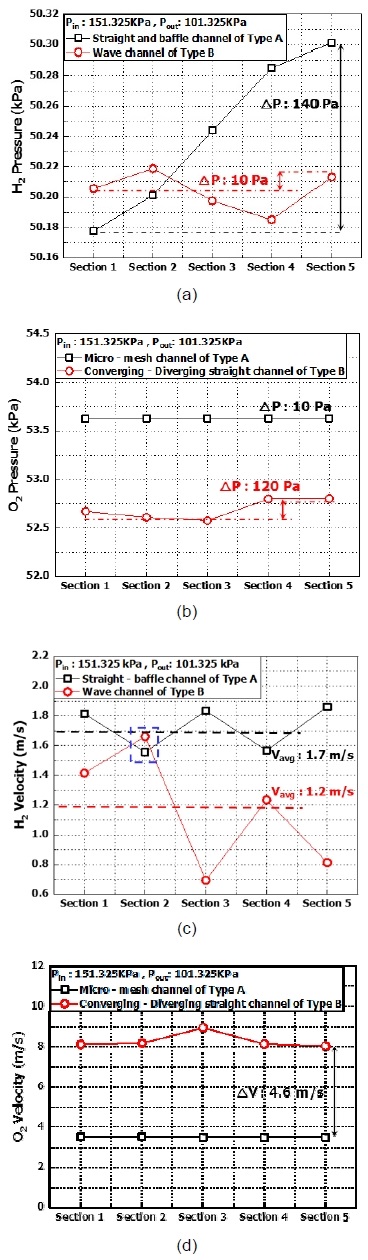
Spatially averaged pressure and velocity comparison in two bipolar plates each condition. (a) Comparison pressure in H2 channel. (b) Comparison pressure in O2 channel. (c) Comparison velocity in H2 channel. (d) Comparison velocity in O2 channel.
수소 유로 영역은 section 5에서 연료인 수소가 유입되어 section 1에서 배출되는 과정을 가진다. Fig. 9(a)에서 내부 압력을 비교한 경우를 보면 장공형 베플이 있는 직선형 유로는 배출 과정 동안 0.14 kPa의 변동을 보여주고 물결 유로는 0.01 kPa의 더 낮은 변동을 보여준다. Fig. 9(c)에서 유속을 비교한 경우 직선형 유로에서 평균 유속이 1.7 m/s, 물결 유로에서 1.2 m/s로 나타났다. 차압과 유속을 고려하였을 때 높은 차압과 유속을 가지는 직선형 베플 유로에서 효율적인 가스 분배와 높은 열전달로 연료전지의 화학 반응으로 생성된 열을 낮추어 온도 균형을 유지하는 데 유리할 것으로 판단된다. 하지만 내부 압력 차가 높게 나타날수록 압축기와 펌프 같은 주변 기기에서 추가적인 에너지 소모가 필요하다20). Type B의 수소 영역 내 물결 유로는 section 1, 2에서 유체의 흐름을 집중시켜 유속이 역전되었는데 이는 수소의 축적을 초래하여 연료전지 성능을 저하시킬 수 있다.
산소가 흐르는 미세 공극 유로와 확관 및 축관 직선형 유로에서 결과를 나타낸 Fig. 9(b), (d)의 경우 section 1에서 공기가 유입되어 section 5에서 배출되는 과정을 가진다. 내부 압력을 비교한 경우 type A 분리판에서 미세한 공극으로 인하여 배출 과정 동안 압력이 53.6 kPa로 유지되었다. Type B의 직선형 유로는 유입 유량이 미세 공극 유로보다 많지만 더 낮은 압력인 52.5 kPa로 유지되었다. 이는 확관과 축관의 유로 형상이 반응물의 균일한 분포를 만들었기 때문으로 판단된다. 유속을 비교할 경우 type B의 직선형 유로가 type A의 미세 공극 유로와 비교하여 배출 영역인 section 5에서 4.6 m/s 더 높은 유속을 보여줬다.
결과적으로 확관과 축관 직선형 유로는 배출 과정 동안 균일하고 낮은 압력과 높은 배출 유속을 보여주었다. 이는 펌프와 같은 주변 기기에 불필요한 에너지 낭비를 막아 기생 전력을 줄이며 전기화학 반응으로 생성된 물이 침전되는 현상을 방지한다. 따라서 연료전지의 전체적인 시스템의 에너지 효율과 수명 향상 목적을 위한 최적화 설계 시 물결 유로는 지양할 필요가 있으며 직선형 및 확관과 축관되는 유로 형상은 지향될 필요가 있다.
3.4 균일지수 비교 분석
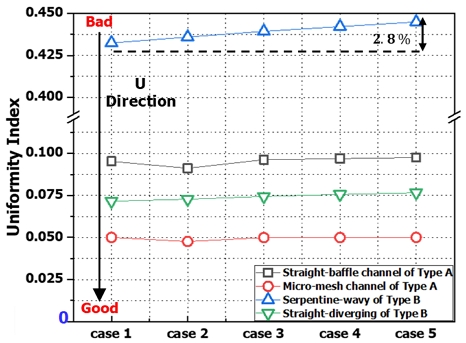
연료전지의 효율적인 에너지 활용과 전기화학 반응을 증가시키기 위해서 분리판 내부의 반응 면적을 늘려야 한다21). 이런 반응 면적은 반응물인 수소와 산소의 균일한 분포가 영향을 미친다22). Table 4와 Fig. 10은 식 (6)을 통해 유입 유량의 변화에 따른 각 분리판 내부 값을 정량적 수치와 그래프로 나타내었다. 이는 균일지수로 각 유로의 질량 유량을 전체 질량 유량의 평균으로 나눈 값이기 때문에 수치가 0에 수렴할수록 반응 물질의 분포가 균일함을 의미한다.
수소 유로 영역에서 균일지수를 평가한 결과 type A의 분리판이 case 2의 유입 유량 조건에서 균일 지수 0.0912의 값을 보여줬다. 이는 직렬형 유로 분리판에서 장공형 베플이 유동을 방해하였음에도 유입된 수소가 전체 유로에 매우 균일하게 분포되었음을 의미한다. 이는 40개의 유로 중 베플이 있는 유로는 2개의 유로이며 나머지 38개의 유로는 직선형 유로이기 때문에 직선형 유로의 영향이 더 지배적인 것으로 판단된다. 이와 반대로 type B 분리판은 0.436의 높은 균일지수 값을 보여주었는데 이는 사문형 물결 유로로 인해 수소의 정체와 특정 유로에 집중이 발생하여 전체 반응 면적에 균일한 분배가 일어나지 않은 것으로 판단된다.
또한 Fig. 10의 그래프와 같이 case 1에서 case 5로 유입 유량이 증가할수록 균일 지수는 2.8% 상승하는데 이는 유량의 증가로 더 많은 축적과 반응 물질이 집중되는 영향이 커져 불균일한 분포가 증가한 것으로 분석된다.
산소 유로 영역에서 균일지수를 평가한 경우 type A의 분리판이 case 2에서 0.0477로 가장 낮은 균일지수 값을 보여주는데 이는 미세 공극에 의해 유로 전체에 산소가 고르게 분포하기 때문으로 판단된다. Type B의 확관과 축관이 되는 유로의 균일 지수는 미세 공극 유로에 비해 높은 것으로 나타나 매우 균일한 유동을 만들었다고 평가할 수 있다.
따라서 물결 유로를 제외한 유로 형상들은 유입 유량의 증가에도 균일한 유동을 형성시킨 것으로 판단되며, 특히 직선형 유로는 반응 물질의 종류에 상관없이 항상 균일한 유동 분포를 형성하는 것으로 파악된다.
4. 결 론
본 연구는 연료전지의 성능 향상을 위한 기초 데이터를 확보하기 위해서 PEMFC의 구성 요소 중 하나인 분리판에서 역설계를 진행하였고 유로 형상과 유입 유량 변화에 따른 내부 유동 특성 및 공간 평균과 균일지수를 분석하여 다음과 같은 결론을 얻었다.
1) 유입 유량의 증가는 유로 내부 차압과 배출 유속을 증가시키는 주요 인자로 판단되며 유로 단면적의 증감은 질량 보존 법칙을 유지하기 위하여 시스템 내의 노즐과 디퓨저 효과를 발생시킨다.
2) 장공형 베플은 유동의 흐름을 방해하고 유속을 감소시키는 원인이 되며 사문형 물결 유로는 반응 물질의 축적을 발생시켜 불균일한 분포를 형성시켰다. 미세한 공극 유로는 압력과 배출 유속을 균일하게 유지하며 확관 및 축관 직선 유로는 정체와 확산을 통해 유로 전체에 일정한 압력과 배출 유속을 만드는 것으로 파악된다. 이러한 유로 형상의 특성은 유체 흐름 최적화와 반응 효율성 개선을 위한 중요한 설계 인자로 고려된다.
3) 직선형 유로와 같이 높은 차압을 발생시키는 유로는 수소의 효율적인 배출을 기대해 볼 수 있으나 펌프와 압축기와 같은 주변 기기의 기생 전력이 발생할 수 있다.
4) 연료전지 시스템에서 높은 에너지 효율과 물의 침전으로 인한 flooding 현상을 방지하기 위한 분리판 최적화 설계 시 물결 유로와 장공형 베플은 지양하고 직선형 유로와 미세 공극 및 축관, 확관 유로 형상을 채택하면 향후 연료전지 출력 성능 향상에 도움이 될 것으로 판단된다.
Acknowledgments
본 논문은 교육부와 한국연구재단의 재원으로 지원을 받아 수행된 3단계 산학연협력 선도대학 육성사업(LINC 3.0)의 연구 결과입니다.
References
-
Z. P. Cano, D. Banham, S. Ye, A. Hintennach, J. Lu, M. Fowler, and Z. Chen, “Batteries and fuel cells for emerging electric vehicle markets,” Nature Energy, Vol. 3, 2018, pp. 279-289.
[https://doi.org/10.1038/s41560-018-0108-1]

- F. Barbir, “PEM fuel cells: theory and practice,” 2nd ed, Elsevier, Netherlands, 2013.
-
D. Musse and D. Lee, “Computational evaluation of PEMFC performance based on bipolar plate material types”, Energy Reports, Vol. 11, 2024, pp. 4886-4903.
[https://doi.org/10.1016/j.egyr.2024.04.052]

- S. Ahn, K. Oh, and H. Ju, “Numerical study on comparison of serpentine and parallel flow channel in high-temperature proton exchange membrane fuel cells”, Journal of Hydrogen and New Energy, Vol. 29, No. 1, 2018, pp. 41-55.
-
J. Lee, N. Lee, K. Lim, J. Choi, and H. Ju, “Numerical study on the cathode channel width ratio for improving performance of a passive air cooled PEMFC”, The KSFM Journal of Fluid Machinery, Vol. 23, No. 1, 2020, pp. 40-48.
[https://doi.org/10.5293/kfma.2020.23.1.040]

- Y. S. Jung, “Effect of separator flow path change on the fuel cell performance [Master's thesis]”, Changwon: Kyungnam University, 2022.
-
J. B. Lu, G. H. Wei, F. J. Zhu, X. H. Yan, and J. L. Zhang, “Pressure effect on the PEMFC performance”, Fuel Cells, Vol. 19, No. 3, 2019, pp. 211-220.
[https://doi.org/10.1002/fuce.201800135]

-
J. J. Hwang, M. M. Dlamini, F. B. Weng, T. Chang, C. H. Lin, and S. C. Weng, “Simulation of fine mesh implementation on the cathode for proton exchange membrane fuel cell (PEMFC)”, Energy, Vol. 244, Pt. A, 2022, pp. 122714.
[https://doi.org/10.1016/j.energy.2021.122714]

-
P. von Tettau, S. Sterlepper, P. Mauermann, M. Wick, S. Tinz, M. Jesser, M. Walters, and S. Pischinger, “Laboratory assessments applied to mass-produced automotive fuel cells”, International Journal of Hydrogen Energy, Vol. 52, Pt. D, 2024, pp. 1127-1136.
[https://doi.org/10.1016/j.ijhydene.2023.10.309]

-
A. Iranzo, J. M. Gregorio, P. Boillat, and F. Rosa, “Bipolar plate research using computational fluid dynamics and neutron radiography for proton exchange membrane fuel cells”, International Journal of Hydrogen Energy, Vol. 45, No. 22, 2020, pp. 12432-12442.
[https://doi.org/10.1016/j.ijhydene.2020.02.183]

-
Y. D. Lee, J. Y. Kim, D. J. Yoo, H. Ju, and H. Kim, “Review of research trend in fuel cell: analysis on fuel-cell-related technologies in electrode, electrolyte, separator plate, stack, system, balance of plant, and diagnosis areas”, Journal of Hydrogen and New Energy, Vol. 31, No. 6, 2020, pp. 530-545.
[https://doi.org/10.7316/KHNES.2020.31.6.530]

-
J. H. Jo and W. T. Kim, “Numerical analysis of the effect of operating pressure and operating temperature on PEMFC performance,” Journal of the Korean Society of Mechanical Technology, Vol. 15, No. 2, 2013, pp. 247-253.
[https://doi.org/10.17958/ksmt.15.2.201304.247]

-
W. R. W. Daud, R. E. Rosli, E. H. Majlan, S. A. A. Hamid, R. Mohamed, and T. Husaini, “PEM fuel cell system control: a review”, Renewable Energy, Vol. 113, 2017, pp. 620-638.
[https://doi.org/10.1016/j.renene.2017.06.027]

-
M. Tawalbeh, S. Alarab, A. Al-Othman, and R. M. N. Javed, “The operating parameters, structural composition, and fuel sustainability aspects of PEM fuel cells: a mini review”, Fuels, Vol. 3, No. 3, 2022, pp. 449-474.
[https://doi.org/10.3390/fuels3030028]

-
S. Maharudrayya, S. Jayanti, and A. P. Deshpande, “Pressure losses in laminar flow through serpentine channels in fuel cell stacks”, Journal of Power Sources, Vol. 138, No. 1-2, 2004, pp. 1-13.
[https://doi.org/10.1016/j.jpowsour.2004.06.025]

-
L. Rostami, M. Haghshenasfard, M. Sadeghi, and M. Zhiani, “A 3D CFD model of novel flow channel designs based on the serpentine and the parallel design for performance enhancement of PEMFC”, Energy, Vol. 258, 2022, pp. 124726.
[https://doi.org/10.1016/j.energy.2022.124726]

-
X. Li and I. Sabir, “Review of bipolar plates in PEM fuel cells: flow-field designs”, International Journal of Hydrogen Energy, Vol. 30, No. 4, 2005, pp. 359-371.
[https://doi.org/10.1016/j.ijhydene.2004.09.019]

-
A. P. Manso, F. F. Marzo, J. Barranco, X. Garikano, and M. G. Mujika, “Influence of geometric parameters of the flow fields on the performance of a PEM fuel cell. A review”, International Journal of Hydrogen Energy, Vol. 37, No. 20, 2012, pp. 15256-15287.
[https://doi.org/10.1016/j.ijhydene.2012.07.076]

-
T. Wilberforce, Z. El-Hassan, F. N. Khatib, A. Al Makky, J. Mooney, A. Barouaji, J. G. Carton, and A. G. Olabi, “Development of bi-polar plate design of PEM fuel cell using CFD techniques”, International Journal of Hydrogen Energy, Vol. 42, No. 40, 2017, pp. 25663-25685.
[https://doi.org/10.1016/j.ijhydene.2017.08.093]

-
W. T. Lee, D. T. Vuong, and H. C. Kim, “Performance change of PEMFC according to flowfield”, Journal of the Korean Society of Manufacturing Technology Engineers, Vol. 33, No. 4, 2024, pp. 200-206.
[https://doi.org/10.7735/ksmte.2024.33.4.200]

-
H. Heidary, M. J. Kermani, and B. Dabir, “Influences of bipolar plate channel blockages on PEM fuel cell performances”, Energy Conversion and Management, Vol. 124, 2016, pp. 51-60.
[https://doi.org/10.1016/j.enconman.2016.06.043]

- P. J. Smith, W. R. Bennett, I. J. Jakupca, R. P. Gilligan, and L. G. Edwards, “Effect of reactant pressure on proton exchange membrane fuel cell performance,” NASA Technical Reports Server, 2021. Retrieved from https://ntrs.nasa.gov/citations/20205011192, .