FERPM을 적용한 바이오매스 촤의 전산해석적 연구

1. 서 론

에너지를 생산하기 위한 다양한 수단 중 석탄은 다른 화석 연료보다 저렴하고 풍부한 자원으로 잘 알려져 있다. 석탄을 이용한 석탄화력발전은 오랫동안 사용되어 온 발전기술인만큼 연료 혼합기술과 연소 기술 수준이 안정단계에 있는 발전방식이며 세계 전력생산의 약 30% 이상을 차지할 정도로 지금까지는 세계적으로 많은 양의 에너지가 석탄에 의존하고 있다¹⁾. 후단 설비기술이 점차 발전되면서 석탄화력발전이 수반하는 대기오염 배출물인 질소산화물(NOx)과 황산화물(SOx) 배출은 대폭 줄어들었지만 이산화탄소 배출은 아직 문제가 되고 있다²⁾. 이러한 석탄화력발전의 문제점을 해결하기 위한 여러 방안 중 하나로 많은 연구자들은 바이오매스 혼소기술에 주목한다. 혼소기술은 전력생산을 위해 재생 가능한 바이오매스 연료를 석탄과 함께 직접 연소하는 것을 의미한다³⁾. 특정 생물 유래 바이오매스는 매우 빠른 성장 속도를 가지므로 에너지 생산에 정기적인 연료 공급원으로 사용할 수 있다. 바이오매스 연료는 연소중 방출하는 CO₂를 생장 과정에서 흡수함으로써 탄소 중립적인 연료로 간주되며 석탄과 함께 혼합하여 연소하면 연소 시 방출되는 화석 연료 기반의 CO₂ 순 배출량이 줄어드는 것으로 간주된다⁴⁾. 또한 바이오매스 연료는 석탄보다 상대적으로 연료의 황 함량과 질소 함량이 낮은 특성이 있어 석탄을 바이오매스로 대체함으로써 SOx와 NOx 배출량을 줄일 수 있는 이점이 있다⁵⁾.

연구자들은 발전용 보일러에서 석탄의 일부를 바이오매스로 대체하기 위한 연구를 진행하였으며^6-8), 많은 경우에 실제 형상에 대한 3차원 전산해석적 방법으로 수행된다. 보일러 내부에서의 유동과 열, 화학적 변화에 대한 예측 없이 현장에 적용하는 것은 여러 불확실한 요소를 동반할 수 있지만 전산해석은 적은 비용으로 합리적 측면에서의 통찰을 제공한다. 해석의 정확도를 높이기 위해서는 모델과 입력값을 적절하게 선정하는 것이 중요하며, 특히 바이오매스의 연소 특성은 석탄과 다를 수 있으므로 그에 맞는 열적 거동을 파악하는 것이 중요하다^9,10). 바이오매스의 연소에 관한 연구는 지금까지 광범위하게 이루어졌지만^11-13), 바이오매스 촤에 대해서는 아직 제한적이다. 바이오매스 촤는 석탄 촤보다 입자 구조가 불규칙하며, 촤 내의 무기물 구성으로 인해 석탄 촤와 다른 연소 거동을 나타낸다. 따라서 정확도 높은 예측을 위하여 바이오매스 촤 연소 거동 모델이 필요하다¹⁴⁾.

고체 연료의 연소를 예측하는 모델은 일반적으로 연소 초반 및 중반부에는 적절한 예측을 제공하지만, 연소 후반부에는 회분으로 인한 희석 효과, 입자내 반응성 차이, 열 어닐링 등에 의하여 반응성이 감소하는 현상을 보인다^15-17). 일부 연구자들은 이 현상을 예측하기 위해 연소 후반부의 물리적 현상을 관찰하여 새로운 연소 모델을 제시하였다^16,18). Lisandy 등¹⁸⁾은 석탄과 바이오매스 촤의 열 중량분석으로 얻은 데이터를 통해 random pore model (RPM)¹⁹⁾을 보완시킨 flexibility-enhanced RPM (FERPM)을 제안하였다. FERPM은 RPM의 다공성 입자의 반응도에 따라 내부 기공 구조가 변화한다는 기본 이론에 더하여, 연료 종류에 따른 반응속도의 차이를 나타낼 수 있는 실험 데이터 기반의 파라미터를 도입하여 연소성을 효과적으로 예측한다. 특히 바이오매스의 촤 연소에 있어 기존의 연소 모델에 비하여 우수한 정확도를 보이나 아직 전산해석에 적용한 사례는 없다.

일반적으로 상용 전산해석 프로그램인 Ansys Fluent에서 제공하는 촤 연소 모델은 intrinsic model, diffusion limited model, kinetic/diffusion limited model이 있다. Intrinsic model은 Smith²⁰⁾의 이론을 발달시킨 모델이며 촤 입자 내부 기공으로의 산소 확산에 의한 산화 반응을 나타낸다. 이 모델은 kinetic이 지배적인 저온 영역대의 반응을 설명하기에 적합하며 Zone I 반응으로 분류된다. Diffusion limited model은 kinetic에 의한 화학 반응속도론을 고려하지 않고 오직 확산에 의한 산화 반응을 기술하는 모델이다²¹⁾. 이 모델은 촤 반응이 산소 확산속도보다 상당히 빠른 고온 영역대의 반응을 설명하기에 적합하며 Zone III 반응으로 분류된다. 반면에 kinetic/diffusion limited model은 화학 반응속도론과 표면 확산을 모두 고려하여 반응속도를 결정하며 Baum과 Street²¹⁾ 그리고 Field²²⁾에 의해 제안된 모델이다. 이 모델은 Zone II 반응으로 분류되며 비교적 넓은 온도 영역대에서 합리적인 결과를 제공하여 석탄 및 바이오매스 연소 전산해석에서 가장 폭넓게 사용되는 모델이다.

본고에서는 FERPM을 산업용 보일러에 적용하기에 앞서 고체 연료의 동적 연소 실험 장치인 drop tube furnace (DTF) 전산해석에 적용하였으며, 그 과정에서 ansys fluent를 사용하여 3차원 전산해석을 수행하였다. 그리고 FERPM과 기존에 제공되는 촤 연소 모델 사용에 따른 연소 과정의 차이를 비교분석 하였다.

2. 수치해석 및 실험방법

2.1 DTF 장치 및 수치해석 형상

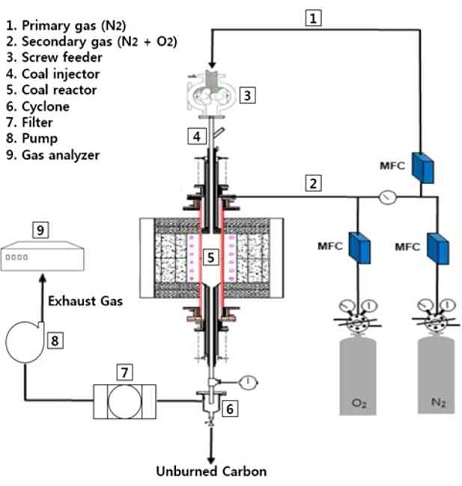
바이오매스 연료의 연소성과 연소 과정을 확인하기 위해 고체 연료의 동적 연소 실험 장비인 DTF를 사용하였다. 일반적으로 DTF의 입자 가열 속도는 산업용 석탄 연소기(10⁴~10⁵K/s)에서 발생하는 것과 비슷하다²³⁾. Fig. 1은 DTF 장치의 개략도를 나타내었다²⁴⁾. DTF는 주입부, 반응부, 포집부로 구분되며 DTF 장비의 상부에는 주입부로부터 바이오매스 연료가 주입되며 이송 가스와 반응 가스가 투입된다. DTF의 반응부는 내부 직경이 0.07 mm, 길이 0.3 m의 알루미나 튜브와 Super Kanthal 발열체로 구성이 되어있으며 균일한 온도 유지가 가능하다. DTF 하부의 포집부는 연료가 연소된 후 남은 회분과 미연분을 포집하는 역할을 한다.

Fig. 1.

Schematic diagram of the DTF

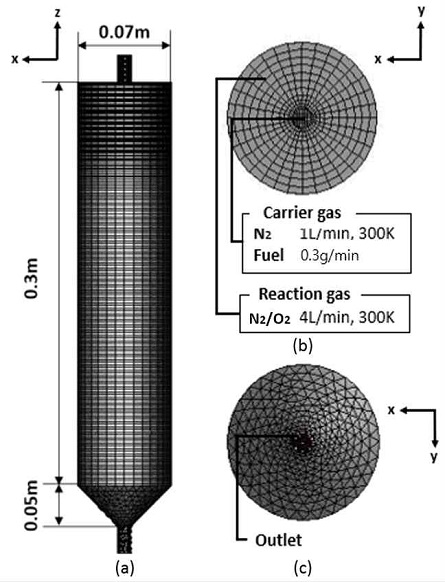
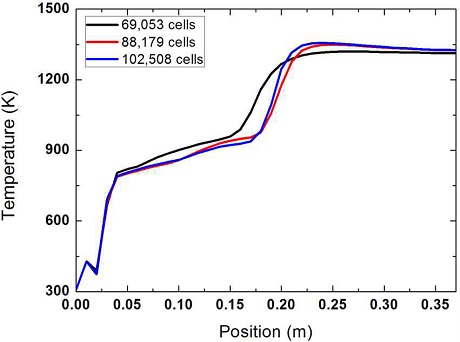
Fig. 2는 DTF 장치를 토대로 전산해석을 수행하기 위해 Gambit 2.4.6을 사용하여 3D 형상과 격자를 구성한 것을 나타낸다. DTF 장치와 동일한 치수로 모델링 되었으며 DTF 상부에서 0.3 g/min의 바이오매스를 상온의 수송 가스(N₂)와 함께 공급한다. 그리고 연료 주입구 바깥쪽에서 연소에 필요한 상온의 반응 가스(N₂/O₂)를 공급한다. 총 유량은 5 L/min이며, 수송 가스는 1 L/min 반응 가스는 4 L/min로 공급된다. DTF 형상의 상부로부터 연료와 가스가 주입되어 하부로 빠져나가는 축 방향 유동 해석에 알맞게 주 반응영역은 모두 육면체 격자로 구성되었고 하부 출구 부분은 사면체 격자로 구성되었다. 또한 수치적 안정성을 위해 DTF 형상의 중심축에 대하여 균일하게 방사형으로 뻗어져 나가는 형태를 나타내며 급격한 반응이 일어나는 DTF 장치의 상부에는 조밀한 격자를 생성하였다. 계산에 적절한 격자의 수를 결정하기 위해 동일 조건에서 바이오매스 연소 테스트가 진행되었으며 DTF의 1차 유입구로부터의 위치에 따른 단면 온도분포 결과를 Fig. 3에 나타내었다. 수렴성과 계산 비용을 고려하여 88,179개의 격자로 전산해석을 수행하였다.

Fig. 2.

Geometry and mesh of DTF; (a) front view (b) top view (c) bottom view

Fig. 3.

Mesh test based on temperature distribution along the DTF position

2.2 전산해석 조건

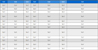
DTF 전산해석 시 사용하는 연료는 목질계 바이오매스 연료인 우드펠릿(wood pellet)을 사용하였다. 우드펠릿의 입자 크기는 일반적으로 석탄 바이오매스 혼소에 사용되는 범위 내에 있는 200 μm로 DTF 상부에서 주입된다. Table 1에 해석에 사용된 연료의 물성치(공업분석, 원소분석, 발열량)를 나타내었다. 공업분석은 air dry (AD), 원소분석은 dry ash free (DAF) basis로 분석한 값이다. 선정된 바이오매스 샘플은 황(sulfur) 성분이 0.1% 미만으로 매우 미미하여 황분에 따른 영향을 고려하지 않았다. 본 전산해석에는 연소 환경에 따른 촤 연소 모델의 차이를 비교하기 위한 목적으로 반응 가스의 산소농도와 DTF장치의 알루미나 튜브 벽면 온도를 달리하여 전산해석을 진행하였다. DTF의 전산해석 경계조건을 Table 2에 나타내었다.

Table 1.

Properties of biomass fuel

Table 2.

Numerical analysis cases and boundary condition

전산해석에서는 기본적으로 유동, 열전달, 화학종 간의 반응 등을 고려해야 하며, 이를 위해 이론적으로 각 물리‧화학적 현상을 지배하는 지배방정식을 계산하게 된다. 또한 고체 연료를 포함하기 때문에 입자상의 연소 과정, 입자와 기체상 간의 질량, 모멘텀, 에너지 전달과 같은 상호작용이 고려된다.

난류 모델은 넓은 범위의 유동에 적용 가능한 realizable k-epsilon 모델을 선정하였으며 많은 경우에서 standard k-epsilon 모델에 비해 좋은 결과를 보인다. 복사 열전달은 석탄 연소 시스템의 열전달 메커니즘에서 중요한 역할을 한다. 이를 고려하기 위하여 모든 범위의 광학 두께에 대해 해석이 가능한 discrete ordinates 모델을 사용하였으며, 이때 흡수 계수는 회색가스가중합법을 적용하였다. 바이오매스 휘발분의 화학반응은 Finite-rate/Eddy-dissipation 모델을 사용하여 예측하였다. 이 모델은 kinetic에 의한 반응 속도와 난류 혼합의 영향을 각각 계산한 후에 작은 값을 반응 속도로 선택한다.

2.3 바이오매스 연소모델

바이오매스 입자의 연소 과정은 입자 가열, 수분 증발, 탈휘발 그리고 촤 연소 순으로 일어난다²⁵⁾. 탈휘발 과정은 입자의 온도가 일정 이상일 때 일어난다. 탈휘발 속도는 일반적으로 아레니우스 식 형태로 표현되며 빈도인자 A와 활성화 에너지 E로 계산된다. 본 연구에서 탈휘발은 single rate model을 사용하여 계산하였으며, 그 과정 동안 입자 내 휘발분 감소량은 다음과 같이 나타낼 수 있다.

$\[ \begin{array}{c}-\frac{{dm}_{p,dev}}{dt}=A_{dev}{e}^{-\left(E_{dev}/RT\right)}\hfill \\ \left[m_p-\left(1-f_{v,0}\right)\left(1-f_{w,0}\right)m_{p,0}\right]\end{array} \]$

(2)

여기서 m_p.dev는 탈휘발 과정 중 입자 질량, m_p,0는 초기 입자질량을 나타내고, f_v,0는 입자의 초기 휘발분 분율, f_w,0는 입자의 초기 수분 분율을 나타낸다. 본 연구에서는 바이오매스 촤의 연소거동을 살펴보기 위함으로 탈휘발 과정은 상대적으로 중요도가 낮다. 따라서 빈도인자와 활성화 에너지는 fluent에서 제공하는 기본값을 채택하였으며 A_dev는 3.82×10⁶s^-1, E_dev는 7.4×10⁷Jkmol^-1을 사용하였다.

탈휘발 과정 동안 방출되는 휘발분의 반응은 2단계의 반응으로 가정하였으며 반응식은 다음과 같다.

$\[ \mathrm{V}\mathrm{o}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{l}\mathrm{e}\mathrm{s}+{\mathrm{O}}_2\to \text{CO}+\text{C}{\text{O}}_{\text{2}}+{\text{N}}_{\text{2}} \]$

(3)

$\[ \text{CO}+0.5\text{C}{\text{O}}_{\text{2}}\to \text{C}{\text{O}}_{\text{2}} \]$

(4)

촤 연소는 휘발분이 입자로부터 모두 방출된 후 일어나는 표면 반응이다. 촤는 완전히 탄소로 이루어졌다고 가정되며, O₂와 반응하여 CO₂를 생성한다. fluent에서 FERPM을 적용하기 위하여 user defined function을 이용하여 코드를 작성하였으며, 다른 촤 연소 모델은 FLUENT 프로그램 내에서 제공되는 것을 사용하여 Table 3에 나타내었다²⁴⁾. Intrinsic model에서 m_p는 입자 질량, η_p와 η_e는 각각 내‧외부 유효계수, k는 반응속도 상수, ρ는 입자 밀도, d_p는 입자 지름 그리고 P_ox,∞는 반응 가스(O₂)의 분압을 나타낸다. Diffusion limited model에서 D_i.m은 확산 계수, Y_ox는 산화제의 질량분율 그리고 T_p와 T_gas는 각각 입자와 가스의 온도를 나타낸다. Kinetic/diffusion limited model에서 A_p는 입자의 표면적, R은 가스 상수, M_w,ox는 산화제의 몰질량 그리고 D_o와 R은 각각 확산 계수와 반응속도상수를 나타낸다. FERPM에서 a, b 그리고 c는 TGA 실험을 통해 얻은 FERPM 파라미터이다. X는 촤 전환율, ψ_FERPM은 입자의 구조 파라미터 그리고 k_FERPM은 FERPM의 반응속도 상수를 나타낸다. 반응속도 상수 또한 빈도인자 A와 활성화 에너지 E로 표현되는 아레니우스식 형태로 나타나며 본 전산해석에서는 Kim 등²⁶⁾의 연구결과를 참고하여 사용하였다. 본 연구에서는 촤 연소 반응에 따른 질량감소를 나타내기 위해 FERPM의 식에 촤 입자 질량의 항을 추가하여 미소시간당 질량감소량의 형태로 나타내었다.

Table 3.

Char combustion model used in simulation

3. 결과 및 고찰

3.1 DTF 온도 분포

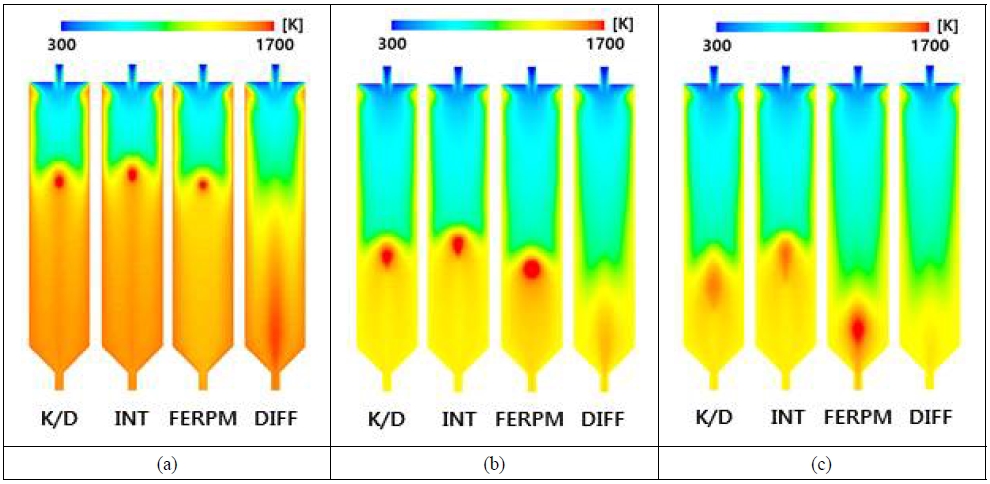
Fig. 4은 각 케이스에 해당하는 DTF 단면 온도분포를 나타낸다. 모든 경우에서 diffusion limited model (DIFF)은 고온 영역대가 DTF 내부에서 길게 나타나는 것으로 보아 전반적으로 연소 길이가 증가하는 것을 알 수 있다. 이는 화학반응이 아닌 확산에 의해 반응이 일어나는 이유로 설명된다. 표면 화학반응이 아닌 산화제(O₂)의 몰 질량과 확산 계수에 지배되어 화학반응보다 상대적으로 연소반응속도가 느린 이유로 판단된다. Kinetic/diffusion limited model (K/D)과 intrinsic model (INT)은 모든 경우에 전반적으로 고온 영역이 상부에 나타나며. FERPM의 경우 case 1, case 2에서 kinetic/diffusion limited model, intrinsic model보다 다소 연소 시작이 늦게 일어난다. 특히 case 3에서 그러한 경향이 두드러지는 것을 확인할 수 있다. 이는 kinetics/diffusion limited model과 intrinsic model은 촤 표면 화학반응에 초점을 맞춘 연소 모델임에 반해 FERPM은 촤 내부 기공발달에 따른 화학반응을 묘사하는 연소 모델이라는 점에서 오는 차이점으로 보인다. Intrinsic model은 촤 표면에서 즉각적인 연소반응이 일어난다고 가정하는 모델이며 kinetics/diffusion limited model은 화학반응과 확산에 의해 반응속도가 결정되는 모델이나, 주변 가스 온도가 증가할수록 확산의 영향이 모델에 반영되기 때문에 현재의 온도 구간에서는 주로 화학반응에 의해 연소반응이 지배받는 것으로 나타난다. FERPM 또한 화학반응을 고려하는 모델이나, 초기 표면반응을 통해 기공이 점차 확장되면서 그에 따라 반응속도가 증가하는 경향을 반영하며 Lisandy 등¹⁸⁾에 따르면 촤 연소반응 중간에 연소 최고 반응속도가 나타난다. 따라서 DTF 단면 온도 분포상으로 FERPM의 경우 다른 표면 화학반응을 다루는 모델에 비해 연소 시작점이 느린 것으로 나타나는 이유는 즉각적인 표면반응이 아닌 점진적인 촤 연소반응 중간에 최고 연소속도가 발생하는 이유로 판단된다.

Fig. 4.

Contours of the temperature in the XZ plane at the centre of DTF

3.2 촤 전환율

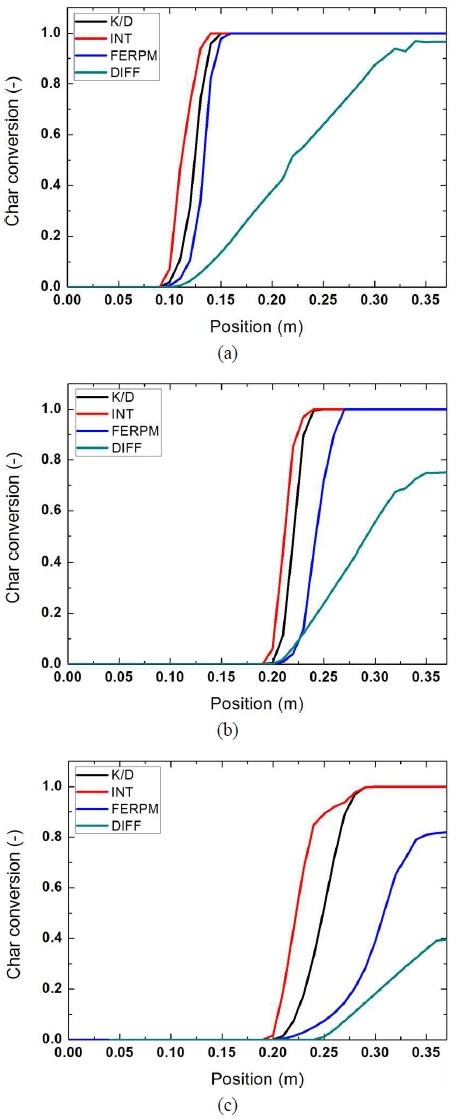
Fig. 5는 DTF 내의 위치에 따른 평균 촤 전환율을 나타낸 것이다. FERPM은 diffusion limited model을 제외한 kinetics diffusion limited, intrinsic model과 비교할 때에 case 1에서 초기 반응속도는 다소 느리지만, 전반적인 반응속도는 비슷한 것을 확인할 수 있다. Case 2에서는 FERPM을 제외한 다른 모델의 경우 초기 반응속도에 큰 영향이 없지만 FERPM은 초기 반응속도가 낮고 이후 반응속도의 증가가 나타난다. 마지막으로 case 3에서 모든 모델들이 전반적으로 반응속도가 떨어지고 특히 FERPM의 초기 반응이 현저히 느려지는 것을 확인할 수 있다. 이는 촤 연소 모델의 반응 메커니즘에 따라 상이한 결과로 나타난다. Intrinsic model은 즉각적인 표면반응으로 초기 촤 전환율이 급격하게 상승하는 것을 나타낸다. 그리고 확산에 의한 반응속도 제한을 받는 kinetics/diffusion limited model 또한 표면 화학반응에 의해 촤 전환율이 급격하게 상승하는 것을 나타낸다. 따라서 표면 산소 농도가 낮은 때에 표면 화학반응 속도에 영향을 주어 다소 느려지는 경향이 나타나는 것으로 판단된다. 또한 diffusion limited model의 경우 산소 확산속도에 반응속도가 결정되며 전반적으로 느린 반응속도로 인해 촤 표면에 충분한 산소가 공급되어 촤 전환이 선형적으로 증가하는 경향이 나타나는 것으로 판단된다. FERPM의 경우 촤 반응 초기에 기공발달이 되지 않아 비표면적이 작은 상태에서 표면 반응속도가 느리다. 이후 반응이 지속됨에 따라 기공 확장으로 인해 비표면적이 증가하여 반응속도가 상승한다. 특히 case 3에서 산소농도가 낮은 환경으로 인해 그에 따라 표면 반응속도는 더욱 느려져 DTF 내에서 반응이 완료되지 못한 것으로 판단된다.

Fig. 5.

Char conversion rate along DTF position; (a) case 1; (b) case 2; (c) case 3

3.3 입자 반응곡선

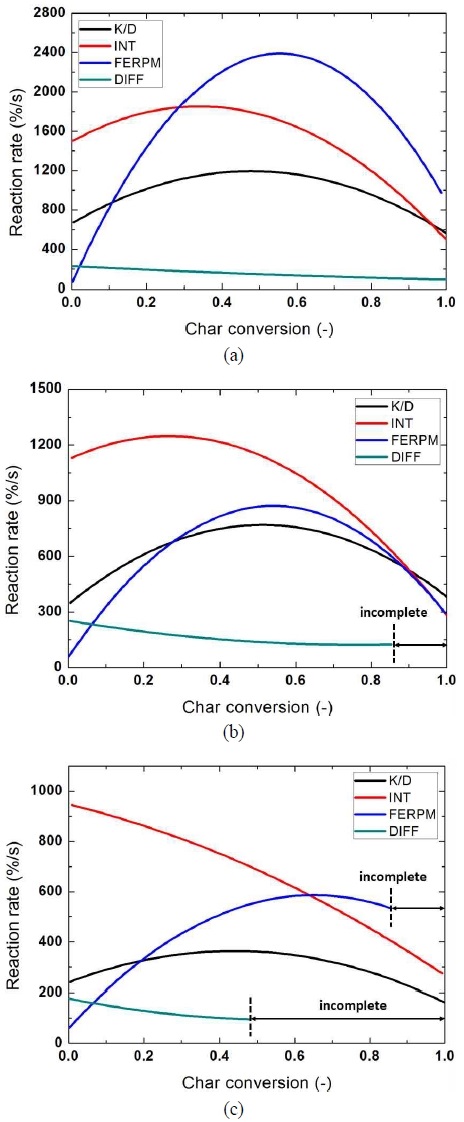
Fig. 6은 DTF 내에서 반응한 입자의 반응속도와 촤 전환율을 나타낸 그래프다. Case 2와 case 3에서 검정색 파선으로 나타낸 부분은 DTF 내에서 반응이 완료되지 못한 채 포집부로 입자가 빠져나간 것을 나타낸다. Intrinsic model의 경우 반응 초기에 최대 반응속도가 나타난 후 반응이 지속될수록 반응속도가 감소한다. 이는 초기에 급격한 촤 표면 화학반응으로 인해 촤 입자 표면의 산소가 희박한 조건이 생성되며 그에 따라 표면 반응속도가 저하되는 것으로 판단된다. Kinetic/diffusion limited model은 intrinsic model에 비하여 초기 반응속도는 다소 느린 것으로 나타나며 이후 반응으로부터 점점 빨라져 촤 전환이 어느 정도 완료된 지점에서 가장 빠른 반응속도를 나타낸 후 다시 감소하는 것을 알 수 있다. Intrinsic model과 달리 표면 화학반응과 산소 확산의 영향을 함께 고려하여 반응속도가 결정되는 이는 산소농도와 화학반응의 영향을 고려한 결과이며 연소 초기에 표면 화학반응으로 연소속도가 상승하고 이후 확산에 의해 연소속도가 제한되는 이유로 판단된다.

Fig. 6.

Char reaction rate over char conversion in DTF; (a) case 1; (b) case 2; (c) case 3

Diffusion limited model의 경우 반응 초기에 가장 빠른 반응속도를 나타내지만 전반적으로 반응이 아주 느린 것을 알 수 있다. 이는 촤 연소가 시작될 때에 촤 표면의 산소농도가 비교적 농후하여 확산에 지배되는 연소 메커니즘이 반응속도 상승의 결과로 이어지는 것으로 보인다. 그러나 이후 연소반응과 함께 산소농도가 감소하여 그에 따라 촤 연소반응 속도에도 영향을 미치게 되어 반응속도가 점점 감소하여 일정해지는 것으로 판단된다. 그런 이유로 case 2와 case 3에서는 불완전 연소가 나타나는 것을 확인할 수 있다. FERPM의 경우 모든 모델 중 초기 반응속도가 가장 느리지만 촤 전환율이 약 0.6인 부근에서 가장 큰 반응속도를 나타내고 다시 감소하는 것을 알 수 있다. 이는 FERPM의 초기 반응속도는 기공이 발달하지 않은 상태에서 반응속도가 느리게 나타나지만, 반응이 지속됨에 따라 촤의 기공발달을 통해 고온의 환경에서 내‧외부 표면의 연소반응으로 최대 연소속도가 가장 빠르게 나타나는 것으로 판단된다. 그에 따라 초기 반응속도가 느린 이유로 급격한 연소가 나타나는 구간까지 시간이 다소 걸리며 case 2의 경우 다소 느린 초기 반응으로 인해 Fig. 4의 고온 영역이 DTF 출구 부근에 나타나며 그에 따라 최대 반응속도가 함께 낮아지는 것을 알 수 있다. 그와 마찬가지로, case 3에서 낮은 산소 농도로 인해 전반적인 연소속도가 전체적으로 감소하며 FERPM은 완전연소가 되지 못하는 것으로 판단된다. Lisandy 등¹⁸⁾의 연구에 따르면 FERPM은 촤 전환율이 약 0.6 이상이 되면 반응속도가 다시 크게 감소하는 것을 나타낸다. 이는 FERPM이 실험적 데이터로부터 얻은 파라미터를 사용하여 실제 촤 연소 과정과 유사하게 묘사하는 이유로 생각된다. 실제 촤 연소과정은 최대 속도가 나타난 이후 반응속도가 다시 감소하게 된다. 이는 반응성이 높은 부분의 우선적으로 연소된 후 남아있는 반응성이 낮은 잔류 물질로 인해 연소가 지연되거나, 반응이 지속될수록 고정탄소가 감소하여 상대적인 회분의 농축으로 인해 반응성이 낮아지는 이유 그리고 열 어닐링 현상 등에 여러 요에 의해 반응성이 낮아지는 것을 실제 실험데이터로부터 얻은 파라미터가 그러한 경향성을 잘 나타내고 있기 때문이라고 판단된다^16,18).

4. 결 론

바이오매스(wood pellet) 촤에 FERPM을 적용하여 DTF 연소 시뮬레이션을 진행하여 intrinsic model, diffusion limited model, kinetics/diffusion limited model과 비교하였다.

FERPM은 촤의 연소 반응으로 인한 내부 기공 확장을 나타내고 입자의 외부 및 내부의 연소반응을 묘사한다. 그에 따라 상대적 저온에서의 화학반응을 반영한 Zone I 연소 모델과 확산속도와 화학반응을 모두 고려한 Zone II 연소 모델과 유사한 경향을 나타낸다. 본 연구를 통해 얻은 결론은 다음과 같다.

1) FERPM은 촤 산화 반응 시 기공 확장을 통한 비표면적 확장으로 반응속도의 증가를 묘사하여 초기 반응속도 지연을 잘 반영한다. 이는 기존 RPM의 수식을 반영하여 입자 기공구조에 초점을 맞춘 모델링의 결과로 생각되며 반응 초기에 기공발달이 되지 않고 비표면적이 작은 상태에서 연소 반응에 따른 기공이 확장으로 인해 비표면적이 증가함으로 인해 반응속도가 상승하고 일정 수준 이상 반응이 일어난 후에 기공 확장에 따른 반응도의 영향이 줄어듦을 나타냈다.

2) 반응속도가 증가한 후 연소 후기에 반응속도가 감소하는 현상을 FERPM 파라미터를 도입하여 묘사한다. 이는 반응성이 높은 부분의 우선적인 연소 후 잔류 물질은 반응성이 낮은 이유로 연소가 지연되거나, 반응이 지속될수록 입자 내부 회의 농축으로 인해 반응성이 낮아지는 이유 그리고 열 어닐링 현상 등에 의해 입자의 후기 연소가 지연되는 복합적인 메커니즘을 TGA 실험을 통해 얻은 FERPM 파라미터가 현상을 대표하는 것으로 판단된다. Diffusion limited model을 제외하고 kinetic/diffusion limited model과 intrinsic model 또한 연소 후기에 반응속도가 감소하는 것을 묘사하지만 표면반응에 의한 전반적인 촤 연소과정은 FERPM에서 특히 잘 묘사되고 있다.

3) 산소농도가 낮은 환경처럼 촤 반응성이 낮은 환경에서 다른 모델에 비해 FERPM이 연소속도가 크게 느려지는 이유는 초기 반응속도가 느리기 때문이다. 기공이 발달하지 않은 초기 촤 상태에서 반응속도가 증가하기까지 다른 모델에 비해 시간이 다소 걸리며 특히 반응도가 낮은 환경에서 초기 반응성이 크게 낮아져 전체 반응속도에 영향을 미치기 때문으로 판단된다.

Acknowledgments

본 연구는 산업통상자원부의 재원으로 한국에너지기술평가원(KETEP)의 지원을 받아 수행하였다(과제번호: 20173010092550).

References

• P. Madejski, “Thermal power plants : new trends and recent developments”, IntechOpen, Poland, 2018, pp. 1-11. [https://doi.org/10.5772/intechopen.69696]
• S. R. Gubba, D. B. Ingham, K. J. Larsen, L. Ma, M. Pourkashanian, H. Z. Tan, A. Williams, and H. Zhou, “Numerical modelling of the co-firing of pulverised coal and straw in a 300 MWe tangentially fired boiler”, Fuel Processing Technology, Vol. 104, 2012, pp. 181-188. [https://doi.org/10.1016/j.fuproc.2012.05.011]
• E. Houshfar, Ø. Skreiberg, D. Todorović, A. Skreiberg, T. Løvås, A. Jovović, and L. Sørum, “NO_x emission reduction by staged combustion in grate combustion of biomass fuels and fuel mixtures”, Fuel, Vol. 98, 2012, pp. 29-40. [https://doi.org/10.1016/j.fuel.2012.03.044]
• M. Sami, K. Annamalai, M. Wooldridge, “Co-firing of coal and biomass fuel blends”, Prog. Energy Combust. Sci., Vol. 27, No. 2, 2001, pp. 171-214. [https://doi.org/10.1016/S0360-1285(00)00020-4]
• K. Savolainen, “Co-firing of biomass in coal-fired utility boilers”, Applied Energy, Vol. 74, No. 3-4, 2003, pp. 369-381. [https://doi.org/10.1016/S0306-2619(02)00193-9]
• R. Pérez-Jeldres, P. Cornejo, M. Flores, A. Gordon, and X. García, “A modeling approach to co-firing biomass/coal blends in pulverized coal utility boilers: synergistic effects and emissions profiles”, Energy, Vol. 120, 2017, pp. 663-674. [https://doi.org/10.1016/j.energy.2016.11.116]
• A. A. Bhuiyan and J. Naser, “CFD modelling of co-firing of biomass with coal under oxy-fuel combustion in a large scale power plant”, Fuel, Vol. 159, 2015, pp. 150-168. [https://doi.org/10.1016/j.fuel.2015.06.058]
• S. Black, J. Szuhánszki, A. Pranzitelli, L. Ma, P. J. Stanger, D. B. Ingham, and M. Pourkashanian, “Effects of firing coal and biomass under oxy-fuel conditions in a power plant boiler using CFD modelling”, Fuel, Vol. 113, 2013, pp. 780-786. [https://doi.org/10.1016/j.fuel.2013.03.075]
• E. Kastanaki and D. Vamvuka, “A comparative reactivity and kinetic study on the combustion of coal–biomass char blends”, Fuel, Vol. 85, No. 9, 2006, pp. 1186-1193. [https://doi.org/10.1016/j.fuel.2005.11.004]
• A. I. Moreno, R. Font, and J. A. Conesa, “Combustion of furniture wood waste and solid wood: kinetic study and evolution of pollutants”, Fuel, Vol. 192, 2017, pp. 169-177. [https://doi.org/10.1016/j.fuel.2016.12.022]
• H. Yang, R. Yan, H. Chen, D. H. Lee, and C. Zheng, “Characteristics of hemicellulose, cellulose and lignin pyrolysis”, Fuel, Vol. 86, No. 12-13, 2007, pp. 1781-1788. [https://doi.org/10.1016/j.fuel.2006.12.013]
• H. Yang, R. Yan, H. Chen, C. Zheng, D. H. Lee, and D. T. Liang, “In-depth investigation of biomass pyrolysis based on three major components: hemicellulose, cellulose and lignin”, Energy Fuels, Vol. 20, No. 1, 2006, pp. 388-393. [https://doi.org/10.1021/ef0580117]
• J. E. White, W. J. Catallo, and B. L. Legendre, “Biomass pyrolysis kinetics: a comparative critical review with relevant agricultural residue case studies”, J. Anal. Appl. Pyrolysis, Vol. 91, No. 1, 2011, pp. 1-33. [https://doi.org/10.1016/j.jaap.2011.01.004]
• M. J. Wornat, R. H. Hurt, K. A. Davis, and N. Y. C. Yang, “Single-particle combustion of two biomass chars”, Symposium (International) on Combustion, Vol. 26, No. 2, 1996, pp. 3075-3083. [https://doi.org/10.1016/S0082-0784(96)80151-2]
• J. K. Sun and R. H. Hurt, “Mechanisms of extinction and near-extinction in pulverized solid fuel combustion”, Proc. Combust. Inst., Vol. 28, No. 2, 2000, pp. 2205-2213. [https://doi.org/10.1016/S0082-0784(00)80630-X]
• R. Hurt, J. K. Sun, and M. Lunden, “A kinetic model of carbon burnout in pulverized coal combustion”, Combust. Flame, Vol. 113, No. 1-2, 1998, pp. 181-197. [https://doi.org/10.1016/S0010-2180(97)00240-X]
• Y. Niu and C. R. Shaddix, “A sophisticated model to predict ash inhibition during combustion of pulverized char particles”, Proc. Combust. Inst., Vol. 35, No. 1, 2015, pp. 561-569. [https://doi.org/10.1016/j.proci.2014.05.077]
• K. Y. Lisandy, G. M. Kim, J. H. Kim, G. B. Kim, and C. H. Jeon, “Enhanced accuracy of the reaction rate prediction model for carbonaceous solid fuel combustion”, Energy Fuels, Vol. 31, No. 5, 2017, pp. 5135-5144. [https://doi.org/10.1021/acs.energyfuels.7b00159]
• S. K. Bhatia and D. D. Perlmutter, “A random pore model for fluid‐solid reactions: I. Isothermal, kinetic control”, AIchE, Vol. 26, No. 3, 1980, pp. 379-386. [https://doi.org/10.1002/aic.690260308]
• I. W. Smith, “The combustion rates of coal chars: a review”, Symposium (International) on Combustion, Vol. 19, No. 1, 1982, pp. 1045-1065. Retrieved from https://che.utah.edu/~ring/ChE-6960/Combustion%20of%20COAL%20CHARS-%20A%20REVIEW.pdf, . [https://doi.org/10.1016/S0082-0784(82)80281-6]
• M. M. Baum and P. J. Street, “Predicting the combustion behavior of coal particles”, Combust. Sci. Technol., Vol. 3, No. 5, 1971, pp. 231-243. [https://doi.org/10.1080/00102207108952290]
• M. A. Field, “Rate of combustion of size-graded fractions of char from a low-rank coal between 1 200°K and 2 000°K”, Combust. Flame, Vol. 13, No. 3, 1969, pp. 237-252. [https://doi.org/10.1016/0010-2180(69)90002-9]
• L. Ma, A. Guo, Q. Fang, T. Wang, C. Zhang, and G. Chen, “Combustion interactions of blended coals in an O₂/CO₂ mixture in a drop-tube furnace: experimental investigation and numerical simulation”, Appl. Therm. Eng., Vol. 145, 2018, pp. 184-200. [https://doi.org/10.1016/j.applthermaleng.2018.09.033]
• B. H. Lee, S. G. Kim, J. H. Song, Y. J. Chang, and C. H. Jeon, “Influence of coal blending methods on unburned carbon and NO emissions in a drop-tube furnace”, Energy Fuels, Vol. 25, No. 11, 2011, pp. 5055-5062. [https://doi.org/10.1021/ef200783q]
• ANSYS, “ANSYS FLUENT 12.0 Theory Guide”, ANSYS Inc., Canonsburg, PA, 2009.
• G. M. Kim, D. G. Lee, and C. H. Jeon, “Fundamental characteristics and kinetic analysis of lignocellulosic woody and herbaceous biomass fuels”, Energies, Vol. 12, No. 6, 2019, pp. 1008. [https://doi.org/10.3390/en12061008]