
상태방정식을 이용한 고압수소 저장을 위한 수소 열역학 물성 계산 및 비교
2020 The Korean Hydrogen and New Energy Society. All rights reserved.
Abstract
One of the technical methods to increase the volumetric energy density of hydrogen is to pressurize the gaseous hydrogen and then contain it in a rigid vessel. Especially for automotive systems, the compressed hydrogen storage can be found in cars as well as at refueling stations. During the charging the pressurized hydrogen into a vessel, the temperature increases with the amount of stored hydrogen in the vessel. The temperature of the vessel should be controlled to be less than a limitation for ensure stability of material. Therefore, the accurate estimation of temperature is of significance for safely storing the hydrogen. In this work, three well-known cubic equations of state (EOSs) were adopted to examine the accuracy in regenerating thermodynamic properties of hydrogen within the temperature and pressure ranges for the compressed hydrogen storage. The formulations representing molar volume, internal energy, enthalpy, and entropy were derived for Redlich-Kwong (RK), Soave-Redlioch-Kwong (SRK), and Peng-Robinson (PR) EOSs. The calculated results using the EOSs were compared with literature data given by NIST. It was revealed that the accuracies of RK and SRK EOSs were satisfactorily compatible and better than the results by PR EOS.
Keywords:
Compressed hydrogen, Equation of state, Enthalpy, Internal energy, Hydrogen density키워드:
압축 수소, 상태방정식, 엔탈피, 내부에너지, 수소 밀도1. 서 론
수소 저장은 수소 산업을 연결하는 가치 사슬의 핵심 요소 중 하나이며, 수소를 에너지 시스템으로 완성하기 위해 해결해야 할 기술적 난점을 지니고 있다1). 에너지로서 수소의 특성을 살펴보면 수소의 단위 질량당 에너지 밀도는 대표적인 화석연료인 가솔린보다 약 3배 높지만 단위부피 당 에너지 함량은 약 1/4이다2). 따라서 수소 연료 자동차에서와 같이 제한된 공간에 충분한 양의 수소를 저장하는 것은 수소 모빌리티 활성화를 위해 해결해야 하는 가장 중요한 문제 중 하나이다. 수소의 부피 에너지 밀도는 압축 또는 액화에 의해 증가될 수 있다. 그러나 이를 포함한 다양한 수소 저장 방안들은 무게, 부피, 에너지 효율, 충전 시간, 비용 및 안전 측면과 관련하여 장점과 단점이 존재하기 때문에 각 기술들은 특성을 살려 개발되고 있으며, 특성에 따른 활용처가 모색되고 있다.
현재 수소 저장 분야에서 비교적 오랜 기간 연구되었으며, 수소 연료 전지 모빌리티에서와 같은 활용 단계에 도달한 기술은 크게 1) 압축수소, 2) 액화수소, 3) 고체 금속 수소화물로 구분된다3-5).
압축수소 저장은 현재까지 가장 성숙한 기술로 인정받고 있다. 그럼에도 불구하고 무게, 부피 저장 효율, 적합한 형태, 시스템 통합 및 비용 절감에 대한 개선이 필요한 상황이다.
액체수소 저장에서 가장 중요한 기술적 관심은 액체의 비등으로 인한 수소 손실을 최소화하는 것이다. 액체수소는 비등점(-253℃)이 매우 낮은 극저온 액체로 저장되기 때문에 액체로의 열전달에 의해 일부 수소가 증발된다. 이 열원은 ortho-para 수소 변환, 복사 가열, 대류 또는 전도 가열일 수 있다. 이 저장 기술은 부피당 저장 밀도에서 큰 효율성을 갖지만 저온을 유지해야하는 특수한 취급 요구사항이 있다.
고체 금속 수소화물은 수소를 금속 원소 또는 합금에 화학적으로 결합시킴으로써 수소를 고체 형태의 화합물로 저장하는 기술이다. 일부는 대기압 이하에서 수소를 흡착한 다음 가열될 때 상당히 높은 압력에서 수소를 방출할 수 있기 때문에 수소화물은 압축 저장이나 액화 저장과는 다른 특성을 지니고 있다. 또한 선정된 합금의 종류에 따라 광범위한 작동 온도 및 압력을 설정할 수 있다. 각 합금은 사이클 수명 및 반응열과 같은 서로 다른 성능 특성을 가지고 있다. 금속 수소화물은 저압 저장, 적합한 모양 및 합리적인 부피 저장 효율의 장점을 제공하지만 질량당 저장량이 크지 않으며 수소 저장과 방출 과정에서 출입되는 열을 관리해야 하는 단점이 있다.
압축수소는 다른 기술들에 비해 기체수소 형태로서의 상대적 단순성, 빠른 충전 가능성 및 낮은 인프라 영향성으로 인해 모빌리티 시스템의 수소 저장 방안으로 고려되고 있다.
압축수소는 밀폐된 탱크 시스템에 약 20-50 kg/m3의 부피 밀도와 약 5-10%의 중량 밀도(kg H2/kg tank)로 수소를 저장할 수 있다6). 자동차 시스템의 경우, 국제적으로 차량용 기체수소 저장에 대한 표준 압력은 70 MPa (700 bar)로 합의되었다. 또한 수소 충전소에서도 적은 비용으로 대규모의 수소를 저장하기 위해 고압 조건에서 수소를 사용하고 있다.
기체수소를 고압 상태로 가압하여 저장하는 과정에서는 열 발생이 수반된다. 한정된 저장 용기의 부피 내로 지속적인 기체수소의 유입은 저장 용기 내 기체의 압축을 유발하고 이 과정은 온도 상승을 동반하게 된다. 또 다른 열 발생 원인은 유입되는 수소 기체의 엔탈피가 저장 용기 내에서는 속도가 0이 되는 상태로 정지하며 내부에너지로 전환되는 과정에서 발생한다.
경량 수소 연료 전지 차량의 경우 70 MPa의 수소 저장을 위하여 Type IV의 저장 탱크가 사용된다. Type IV 수소 저장 탱크는 플라스틱 라이너를 포함하고 있는 복합소재로 제작된다. 이 때문에 라이너인 고밀도 폴리에틸렌(HDPE)의 성능 저하를 막기 위하여 수소 충전 과정에서 온도는 -40~85℃에서 안정적으로 유지되어야 한다7,8). 차량 내 수소 저장 탱크의 온도를 제한 조건 이내로 맞추기 위해 충전소에서는 수소의 온도를 미리 낮추고 유량을 일정 수준 이하로 조절하게 된다9,10).
차량 내로의 수소 충전을 비롯한 압축수소의 저장에 대한 안전성 확보를 위해서는 압축수소의 거동을 정확히 모사할 필요가 있다. 압축수소의 온도 상승은 앞서 언급한 것과 같이 압축에 의한 온도 상승과 에너지 전환에 의한 온도 상승으로 구분된다. 따라서 온도와 압력에 따른 수소의 부피와 엔탈피 및 내부에너지를 모사하는 수식을 검증하는 것은 압축수소 저장 방법의 활용을 위해 필수적인 과정이다. 본 연구에서는 일반적으로 거의 모든 상업용 공정 모사 전산툴에 공통적으로 포함되어 있는 상태방정식(equation of state, EOS)들을 활용하여 수소의 부피를 계산하고 잔류성질(residual property) (또는 편차함수[departure function]) 방법을 활용하여 수소의 내부에너지, 엔탈피 및 엔트로피의 열역학 물성들을 계산하고 문헌 데이터와 비교 분석하여 공정 모사 전산툴을 활용할 경우 적절한 방법을 선택할 수 있는 방안을 제시하고자 한다.
2. 상태방정식
고압 상태의 수소 거동을 모사하기 위해서는 실제 기체에 적용되는 EOS를 사용해야 한다. 수소에 대해서는 실험 자료들을 정확히 모사하기 위해 많은 매개변수들을 포함하고 있는 수소 기체만을 위해 사용되는 EOS들이 제안되었다11-13). 그러나 이와 같은 상태방정식들은 공정 모사 소프트웨어에 삽입되어 활용되기 어려운 형태를 취하고 있다.
공정 모사에 사용되는 소프트웨어에는 일반적으로 다양한 화학공정에 활용도가 높은 EOS들이 포함되어 있다. 공정 모사 소프트웨어들을 사용하면 이러한 EOS를 이용하여 화학반응, 화합물 분리와 같은 공정들에 대한 수치적 결과를 얻을 수 있다. 따라서 단순히 고압 기체의 물성에 관심을 두는 것이 아니라 추후 수소 생산, 이송, 활용에 이르는 과정에 대한 모사를 고려한다면 일반적인 공정 모사 소프트웨어에 채택된 EOS들을 사용하여 수소의 물성을 계산하고 평가하는 과정이 필요하다.
공정 모사 소프트웨어에 포함된 다양한 EOS들 중 원하는 공정에 적합한 모델을 선택하는 몇 가지 기준 중에 가장 먼저 생각해야하는 것은 화합물의 극성이다. 화합물이 극성의 성질을 보인다면 일반적인 EOS 중에서도 이를 고려한 EOS가 사용되어야 한다. 그러나 수소와 같이 분자가 극성을 보이지 않는 경우는 단순한 3차 상태방정식이 적용 가능하다. 따라서 본 연구에서는 3차 상태방정식들을 이용하여 고압 수소의 물성을 계산하였으며, 서로의 결과를 비교 평가하였다.
2.1 일반화된 3차 상태방정식
액상과 기상의 PVT 거동을 나타내기 위해 van der Waals가 압력을 몰부피에 대해 3차인 다항식으로 표현하는 식을 제안한 이후 다양한 3차 상태방정식이 개발되었다14).
3차 상태방정식들은 매개변수들을 각각에 맞춰 부여하면 다음과 같은 일반화된 형태의 수식으로 표현할 수 있다15).
| (1) |
위 식에서 R은 기체상수이고 ϵ과 σ는 물질의 종류에 의존하지 않는 상태방정식 상수값들이며, a와 b는 물질의 특성을 반영한 매개변수들이다. 특히 a는 온도 의존성을 지니고 있으며, 온도에 따른 표현 관계식은 상태방정식에 따라 다양한 형식으로 주어진다.
매개변수들은 물질의 임계특성인 임계온도(Tc)와 임계압력(Pc)으로부터 계산될 수 있다. 임계등온선은 임계점에서 몰부피에 대해 수평적으로 변곡한다는 조건을 수학적으로 활용하면 다음과 같이 매개변수들의 표현식을 얻을 수 있다.
| (2) |
| (3) |
위 식들에서 ψ와 Ω는 물질에 무관한, 상태방정식에 따라 변경되는 수치값들이다. 식 (2)의 α는 온도에 의존하는 항으로 상태방정식에 의해 특정되는 수식이다.
3차 상태방정식을 이용하여 유체의 부피를 계산할 경우에는 압력으로 표현된 식 (1)을 변형하는 것이 편리하다. 부피(또는 밀도 ρ)보다 열역학 계산에서는 압축인자 Z (= PV/RT)를 유용하게 사용하고 있으며 식 (1)을 압축인자 형식으로 변형하면 다음과 같이 밀도에 대한 식을 얻을 수 있다.
| (4) |
Z에 대해 정리한 식 (4)의 우변에 나타난 ρ는 P/ZRT이므로 식 (4)는 Z에 대해 3개의 근을 갖게 된다. 이는 3차 상태방정식의 특성으로 식 (4)를 풀게 되면 기상에 대한 값과 액상에 대한 값에 더해 물리적으로 의미가 없는 압축인자값이 얻어질 수 있다. 따라서 식 (4)로부터 반복 계산을 통해 기상에 대한 근을 얻고 싶을 때에는 반복 계산에 적합하게 식을 변형해야 정확한 근에 수렴시킬 수 있게 된다. 이를 위해 식을 다음과 같이 다시 정리하여 사용한다.
| (5) |
| (6) |
| (7) |
상태방정식의 해를 찾기 위한 온도와 압력 조건들은 각각 임계온도와 임계압력 값들로부터 정의되는 환산온도(Tr = T/Tc)와 환산압력(Pr = P/Pc)으로 주어지게 된다.
3차 상태방정식은 van der Waals 식으로부터 발전되어 왔으나 정확도가 높지 않아 실제 공정 모사에는 사용되지 않고 있다. 거의 모든 공정 모사 소프트웨어에 포함하고 있는 3차 상태방정식으로는 Redlich-Kwong (RK) 식, Soave-Redlich-Kwong (SRK) 식, Peng-Robinson (PR) 식이 대표적이다. 이들 세 상태방정식을 사용하기 위해 정의되는 매개변수들은 Table 1에 정리되었다. SRK와 PR에 대해서는 온도와 이심인자(ω)로부터 계산되는 α값이 다음과 같이 주어진다.
| (8) |
식 (8)의 하첨자 EOS는 SRK 또는 PR을 의미하며 각 EOS의 κ는 다음 수식으로 주어진다.
| (9) |
| (10) |
2.2 잔류성질
물질의 열역학적 성질들인 엔탈피(H), 엔트로피(S), 내부에너지(U)는 상태함수이기 때문에 초기 상태와 최종 상태만 정의된다면 변화 과정의 경로와 상관없이 변화량이 계산된다. 따라서 어떤 주어진 상태에서 물성값들을 알게 된다면 어떠한 변화에서도 이러한 열역학적 물성 변화는 계산될 수 있다. 그러나 열역학 자료들이 제한되어 있기 때문에 주어진 상태에서 열역학 성질들을 얻기 위해서는 수학적으로 과정을 따라갈 수 있는 단계적 변화를 고려하게 된다. 이러한 개념으로 잔류 성질(residual property) 또는 편차 함수(departure function)가 도입되어 열역학적으로 활용되고 있다14).
잔류 성질은 실제 성질과 이상기체 성질과의 차이로 MR = M - Mig로 정의된다. 잔류 성질들은 압축인자 식으로부터 유도되며 잔류 내부에너지(UR), 잔류 엔탈피(HR), 잔류 엔트로피(SR)는 다음과 같이 얻어진다.
| (11) |
| (12) |
| (13) |
식 (11)-(13)을 활용하면 각 상태방정식으로부터 직접 활용 가능한 형식의 잔류성질들의 수식을 유도할 수 있으며, 결과 식들은 다음과 같다.
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
| (19) |
| (20) |
| (21) |
| (22) |
위 식들을 이용하면 매개변수들과 주어진 온도와 압력 조건에서 식 (5)를 계산하여 얻은 Z값을 사용하여 잔류 열역학 물성들을 얻을 수 있다.
3. 열역학 물성 계산 및 비교
잔류성질은 이상기체와의 차이를 나타내므로 두 상태에서 실제 기체의 변화 중 압력의 변화를 나타내는 단계에서 사용된다. 반면 온도 변화는 이상기체 상태에서 고려된다. 즉 ‘실제기체(T1, P1) → 실제기체(T2, P2)’의 변화를 ‘실제기체(T1, P1) → 이상기체(T1, Po) → 이상기체(T2, Po) → 실제기체(T2, P2)’의 세 단계로 구분하여 계산할 때 첫 번째와 세 번째 단계에서 잔류성질이 이용된다. 따라서 이상기체에서 온도변화를 나타내는 두 번째 단계를 위해 이상기체 열용량식이 요구된다. 일반적으로 이상기체 열용량은 온도에 대한 다항식으로 주어지며 문헌에서 제시된 식은 다음과 같다16).
| (23) |
식 (23)에서 온도는 K 단위이며 수소에 대해서 a0 = 2.883, a1 = 3.681×10-3, a2 = -0.772×10-5, a3 = 0.692×10-8, a4= -0.213×10-11로 주어져 있다16).
앞서 정리된 3차 상태방정식들을 사용하기 위해서는 식 (2)와 식 (3)에서와 같이 임계온도와 임계압력에서 계산되는 a와 b의 두 매개변수들이 필요하다. SRK와 PR의 경우는 이들 매개변수 이외에 추가적으로 식 (9) 또는 식 (10)에 사용되는 이심인자가 요구된다. 본 연구에서는 비교적 최근 자료들이 수집 정리된 문헌16)의 값들인 임계온도 33.25 K, 임계압력 1.297 MPa, 이심인자 -0.216을 사용하여 3차 상태방정식들을 이용한 계산을 수행하였다.
계산 온도는 충전소의 최저 냉각온도와 수소 저장 탱크의 최대 온도를 고려하여 233.15-359.15 K를 범위로 2 K 간격으로 설정하였다. 압력 범위는 5-875 bar로 하여 Type IV 탱크의 nominal working pressure의 125%까지 계산하였으며, 압력 간격은 10 bar로 하였다. 따라서 각 온도에서 88개의 압력 조건으로 64개의 온도 조건에서 계산을 수행하여 모두 5,632개의 온도-압력 조합의 조건 하에서 계산 결과를 얻었으며 NIST에서 제공하는 데이터와 비교하였다17).
EOS의 계산 결과를 수치적으로 비교하기 위해 다음 식으로 정의되는 평균 상대오차(relative error, RE)를 사용하였다.
| (24) |
위 식에서 M은 몰부피 V (l/mol), 내부에너지 U (kJ/mol), 엔탈피 H (kJ/mol), 엔트로피 S (J/mol/K)를 의미한다. 와 은 각각 NIST 데이터 물성과 동일한 조건에서 상태방정식으로부터 계산된 물성을 나타낸다.
Fig. 1은 온도에 따른 몰부피의 상대오차 결과를 비교하여 표시한 그림이다. 모든 온도 조건에서 SRK EOS가 가장 낮은 상대오차를 보이고 있는 것으로 확인되었다.

Comparison of relative errors on molar volume calculation with temperature for different cubic equations of state
내부에너지, 엔탈피 및 엔트로피에 대한 비교 결과는 Figs. 2-4에 각각 도시하였다. Fig. 2의 내부에너지 계산 결과를 살펴보면 전 온도 영역에서 RK EOS의 계산 결과가 다른 두 EOS 계산 결과보다 우수한 것으로 나타났다. RK EOS는 내부에너지 계산에 뛰어난 정확성을 보이며 모든 온도에서 1% 이내의 오차를 보이고 있다.

Comparison of relative errors on molar internal energy calculation with temperature for different cubic equations of state

Comparison of relative errors on molar enthalpy calculation with temperature for different cubic equations of state

Comparison of relative errors on molar entropy calculation with temperature for different cubic equations of state
엔탈피 계산 결과는 Fig. 3에서 보인 것과 같이 RK와 SRK가 PR보다 높은 정확성을 갖는 것으로 분석되었으며 RK는 SRK에 대해 307 K보다 고온에서는 다소 우수한 것으로 나타났다.
엔트로피는 세 EOS 모두 모든 온도 영역에서 상당히 정확하게 문헌 데이터를 맞추고 있는 것으로 분석되었다. 온도에 따른 오차의 변화를 비교할 수는 있지만 모두 0.4% 이내에 있기 때문에 세 EOS의 정확성을 수치적으로 비교하는 것은 큰 의미가 없을 것으로 보인다.
전체적으로 살펴보면 V, U, H에 대해서는 온도가 증가함에 따라 모든 EOS의 정확도가 증가하며 S의 계산결과는 V, U, H에 비해 상대적으로 더 정확한 것으로 나타났다.
EOS의 비교가 수행된 온도 범위에서 5,632개 데이터에 대한 평균 오차를 정리하여 Table 2에 표시하였다. 모든 물성에 대해서 PR EOS가 가장 낮은 정확도를 보이고 있다. 이전 연구에서는 PR EOS의 매개변수 a에 대한 온도 의존식이 새롭게 정의된 Peng-Robinson-Gasem (PRG) EOS와 본 연구에서 사용한 RK, SRK EOS와 비교였다18). 몰부피에서 PRG는 SRK와 유사한 정확성을 보이며 고온에서는 PRG 다소 우수한 것으로 나타났다. 반면, 수정되지 않은 PR EOS는 다른 EOS와 비교하여 수소에 대해 만족할만한 결과를 제공하지 않고 있다. 일반적으로 공정 모사 프로그램들은 PR EOS를 포함하고 있으나 PRG EOS는 사용자가 작성해야 한다. 이에 따라 PR EOS가 PRG EOS에 비해 더 폭넓게 다양한 분야에 사용되고 있다. 이와 같은 이유로 인해 본 연구에서는 PRG EOS에 대한 계산은 수행하지 않았다.
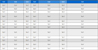
Relative error (%) for calculated results on molar volume (V), internal energy (U), enthalpy (H), and entropy (S) within temperature range
RK과 SRK EOS는 V와 H에 대해서는 SRK가 U와 S에 대해서는 RK가 더 우수한 것으로 분석되었다. 수소를 고압으로 저장할 경우 압축에 의한 온도 상승을 계산하기 위해서는 V를 정확하게 계산할 필요가 있으며 Joule-Thomson 효과를 포함하여 탱크 내로 유입되는 수소의 에너지를 계산하기 위해서는 H를 정확히 추산해야 한다. 이러한 측면에서는 SRK가 더 적절한 것으로 판단될 수 있으나 최종 저장 온도에서의 H는 RK가 SRK보다 정확하게 계산하므로 수소 저장에서 RK와 SRK의 정확성은 저장 과정을 따르는 시뮬레이션을 통한 비교가 뒷받침되어야 할 것이다.
수소 기체의 거동이 이상기체에서 벗어나는 정도를 확인하기 위하여 몰부피가 가장 정확한 SRK EOS로 압축인자(Z)를 계산하여 Fig. 5에 온도 및 압력에 따른 거동을 확인하였다. 이상기체의 경우 Fig. 5의 점선과 같이 온도와 압력에 무관하게 Z = 1이다. 수소의 경우 압력 증가에 따라 Z값이 단순 증가하며 증가되고, 크기는 온도가 높아짐에 따라 감소하는 경향을 보이고 있다.
수소의 U, H와 S에 대한 수치 자료를 비교하기 위해 계산된 결과들 중 일부를 Table 3에 정리하였다. 수소가 압축되는 과정에서 압력과 온도가 동반하여 상승하기 때문에 저온-고압이나 고온-저압 조건은 발생하지 않는다. 이러한 상황을 고려하여 Table 3의 온도-압력 조건은 계산된 범위에서 각각 선형으로 증가하는 간격으로 선택되었다.
NIST에서 제시된 데이터의 H와 S는 기준 끓는점(normal boiling point)에서 포화 액체의 값을 0으로 하여 표시된 값들이다. 기준 상태에서 U의 경우 다음의 열역학 관계식으로부터 구할 수 있게 된다.
| (25) |
엄밀하게 EOS로 계산되는 물성값들은 두 상태의 변화에 따른 물성 차이이다. 따라서 어떤 조건에서 값을 알기 위해서는 기준이 되는 조건에서의 물성값들이 주어져야 한다. 본 연구에서는 233.15 K, 5 bar를 기준 조건으로 하여 NIST 데이터의 물성을 사용하였다. 이에 따라 Table 3에서 표시한 것처럼 기준 조건인 233.15 K, 5 bar에서는 물성값들이 동일하게 된다.
Table 3으로부터 RK EOS는 물성값들을 데이터 보다 조금씩 크게 추산하고 있음을 알 수 있으며, 이에 반해 SRK와 PR EOS는 물성값들을 조금씩 작게 추산하고 있음을 알 수 있다. 따라서 만약 동일한 열용량 값이 사용된다면 RK EOS는 수소 저장 탱크의 온도를 다소 높게, SRK와 PR EOS는 다소 낮게 계산하게 될 것이다. 그러나 계산된 물성의 오차의 크기를 고려하면 이러한 온도 차이는 크지 않을 것으로 예상된다.
4. 결 론
압축된 기체로 수소를 저장하는 방법은 천연가스자동차 연료장치용 용기와 충전 원리의 유사성에 의해 기존 기술의 직접적 적용이 가능하다. 또한, 저장된 수소의 물리적 형태가 단순하고 빠르게 차량용 탱크로 충전이 가능하기 때문에 자동차용 수소 저장의 방안으로 사용되고 있다. 차량 내 수소의 압력은 경량 승용차량의 경우, 차량의 운행 거리를 고려하면 70 MPa 정도의 고압으로 충전되어야 한다. 이에 대응하여 충전소 역시 수소를 고압 상태로 저장하게 된다.
고압 압축수소의 저장 과정에서는 고압 조건에서의 기체 비이상성과 압축 과정에서 발생하는 온도 상승을 고려해야 한다. 열역학적으로 이러한 물성을 추산하기 위해 EOS를 사용하여 온도-압력-부피 거동뿐만 아니라 열적 변화를 모사하는 방법이 활용될 수 있다.
본 연구에서는 수소 기체의 비이상성 거동 모사를 위하여 공정 모사에 사용되는 전산 프로그램에 일반적으로 포함되어 있는 3차 상태방정식을 비교하여 수소 충전 과정의 온도와 압력 조건에서 몰부피, 내부에너지, 엔탈피와 엔트로피의 물성을 계산하였다.
RK, SRK, PR EOS를 사용하기 위하여 각 EOS로부터 물성을 계산하기 위한 식들을 정리하였으며, 문헌 데이터로부터 찾을 수 있는 매개변수들을 사용하여 별도의 회귀분석 없이 열역학 물성들을 계산을 수행하였다.
NIST 자료를 사용하여 233.15-359.15 K의 온도 범위와 5-875 bar의 압력범위 내의 5,632개 조건에서 계산된 값들과 데이터의 오차를 구하여 비교하였다. 전체적으로 PR EOS가 가장 부정확한 것으로 파악되었으며, RK와 SRK EOS는 물성의 종류에 따라 정확도의 우열이 달라졌다. 몰부피의 경우, SRK EOS의 계산 결과가 오차가 가장 작았으나 내부에너지는 RK EOS가 가장 정확한 것으로 나타났다.
압축수소 저장 또는 방출 과정에서 수소의 온도-압력 거동을 모사하는 과정을 RK와 SRK EOS 모두 비교적 정확히 계산할 수 있을 것으로 기대되었으며, 두 EOS 사이의 차이를 수치적으로 비교하기 위해서는 수소 저장 또는 방출 과정의 조건이 주어져야 할 것으로 판단되었다.
Acknowledgments
본 연구는 산업통상자원부(MOTIE)와 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 연구 과제이다(No. 20192910100170).
References
-
A. Züttel, “Hydrogen storage methods”, Naturwissenschaften, Vol. 91, 2004, pp. 157–172.
[https://doi.org/10.1007/s00114-004-0516-x]

-
A. Züttel, A. Remhof, A. Borgschulte, and O. Freidrichs, “Hydrogen: the future energy carrier”, Phil. Trans. R. Soc. A, Vol. 368, 2010, pp. 3329-3342.
[https://doi.org/10.1098/rsta.2010.0113]

-
T. Q. Hua, R. K. Ahluwalia, J. K. Peng, M. Kromer, S. Lasher, K. McKenney, K. Law, and J. Sinha, “Technical assessment of compressed hydrogen storage tank system for automotive applications”, Int. J. Hydrogen Energy, Vol. 36, No. 4, 2011, pp. 3037-3049.
[https://doi.org/10.1016/j.ijhydene.2010.11.090]

-
R. K. Ahluwalia, T. Q. Hua, J. K. Peng, S. Lasher, K. McKenney, J. Shinha, and M. Gardiner, “Technical assessment of cryo-compressed hydrogen storage tank systems for automotive applications”, Int. J. Hydrogen Energy, Vol. 35, No. 9, 2010, pp. 4171-4184.
[https://doi.org/10.1016/j.ijhydene.2010.02.074]

-
B. Sakintuna, F. Lamari-Darkrim, and M. Hirscher, “Metal hydride materials for solid hydrogen storage: a review”, Int. J. Hydrogen Energy, Vol. 32, No. 9, 2007, pp. 1121-1140.
[https://doi.org/10.1016/j.ijhydene.2006.11.022]

-
M. Hosseini, I. Dincer, G. F. Naterer, and M. A. Rosen, “Thermodynamic analysis of filling compressed gaseous hydrogen storage tanks”, Int. J. Hydrogen Energy, Vol. 37, No. 6, 2012, pp. 5063-5071.
[https://doi.org/10.1016/j.ijhydene.2011.12.047]

- Society of Automotive Engineers (SAE), “Fueling protocols for light duty gaseous hydrogen surface vehicles (Standard J2601_201407)”, SAE International, 2014.
- Society of Automotive Engineers (SAE), “Fueling protocols for light duty gaseous hydrogen surface vehicles (Standard J2601_201612)”, SAE International, 2016.
-
M. Monde, P. Woodfiled, T. Takano, M. Kosaka, “Estimation of temperature change in practical hydrogen pressure tanks being filled at high pressure of 35 and 70 MPa”, Int. J. Hydrogen Energy, Vol. 37, No. 7, 2012, pp. 5723-5734.
[https://doi.org/10.1016/j.ijhydene.2011.12.136]

-
R. Ortiz Cebolla, B. Acosta, N. de Miguel, and P. Moretto, “Effect of precooled inlet gas temperature and mass flow rate on final state of charge during hydrogen vehicle refueling”, Int. J. Hydrogen Energy, Vol. 40, No. 13, 2015, pp. 4698-4706.
[https://doi.org/10.1016/j.ijhydene.2015.02.035]

-
E. W. Lemmon and M. L. Huber, “Revised standarized equation for hydrogen gas densities for fuel comsumption applications”, J. Res. Natl. Stand. Technol., Vol. 113, No. 6, 2008, pp. 341-350.
[https://doi.org/10.6028/jres.113.028]

-
N. Sakoda, K. Shindo, K. Shinzato, M. Kohno, Y. Takata, and M. Fujii, “Review of the thermodynamic properties of hydrogen based on existing equations of state”, Int. J. Thermodynamics, Vol. 31, 2010, pp. 276-296.
[https://doi.org/10.1007/s10765-009-0699-7]

-
H. Chen, J. Zheng, P. Xu, L. Li, Y. Liu, and H. Bie, “Study on real-gas equations of high pressure hydrogen”, Int. J. Hydrogen Energy, Vol. 35, No. 7, 2010, pp. 3100-3104.
[https://doi.org/10.1016/j.ijhydene.2009.08.029]

-
J. O. Valderrama, “The state of the cubic equations of state”, Ind. Eng. Chem. Res., Vol. 42, No. 8, 2003, pp. 1603-1618.
[https://doi.org/10.1021/ie020447b]

- J. M. Smith, H. Van Ness, M. Abbott, and M. Swihart, “Introduction to chemical engineering thermodynamics”, 8th ed., McGraw-Hill, USA, 2018.
- B. E. Poling, J. M. Prausnitz, and J. P. O’Connell, “The properties of gases and liquids”, 5th ed., McGraw-Hill, USA, 2001.
- The National Institute of Standards and Technology (NIST), “NIST Chemistry WebBook”, NIST, 2018.
- B. H. Park, “Simulation of temperature behavior in hydrogen tank during refueling using cubic equation of state”, Trans. Korean Hydrogen New Energy Soc., Vol. 30, No. 5, 2019, pp. 385-394.
