심층 신경망 기법을 이용한 고체 산화물 연료전지 스택의 성능 예측 모델
2020 The Korean Hydrogen and New Energy Society. All rights reserved.
Abstract
The performance prediction model of a solid oxide fuel cell stack has been developed using deep neural network technique, one of the machine learning methods. The machine learning has been received much interest in various fields, including energy system mo- deling. Using machine learning technique can save time and cost requried in developing an energy system model being compared to the conventional method, that is a combination of a mathematical modeling and an experimental validation. Results reveal that the mean average percent error, root mean square error, and coefficient of determination (R2) range 1.7515, 0.1342, 0.8597, repectively, in maximum. To improve the predictability of the model, the pre-processing is effective and interpolative machine learning and application is more accurate than the extrapolative cases.
Keywords:
Solid oxide fuel cell, Deep learning, Convolutional neural network, Performance prediction, Regression키워드:
고체 산화물 연료전지, 심층 학습, 합성곱 신경망, 성능 예측, 회귀1. 서 론
다양한 친환경 발전기술 중 연료전지는 전기 화학 반응을 통해 전기를 생성하여 질소 산화물이 발생하지 않으며, 상대적으로 발전효율이 높아 차세대 발전 기술로 주목받고 있다1,2). 특히, 고체 산화물 연료전지(solid oxide fuel cell, SOFC)는 다양한 연료전지 방식 중 가장 고온에서 작동하기 때문에 비가역손실이 작아 가장 높은 발전효율을 보이며, 폐열의 온도 또한 높아 다양한 분야에 활용이 가능하다는 장점을 가지고 있다3). 최근 집중적인 연구개발4-6) 덕분에 현재 고체산화물 연료전지는 연구개발 단계를 벗어나 상용화 제품7,8)이 출시되는 단계에 이르고 있다. 최근 들어서는 고체산화물 연료전지 발전의 효율을 향상시키기 위해 하이브리드 시스템 개발도 활발하게 진행 중이며, SOFC와 엔진을 연계한 발전시스템도 개발되고 있다8).
고체 산화물 연료전지 발전시스템을 개발하는 데 있어, 안정적인 제어 시스템과 고장 감지 및 진단 시스템을 구축하는 것은 매우 중요하며, 이를 위해서는 연료전지 스택의 성능을 정량적으로, 정확하게 예측하는 것이 중요하다. 고체 산화물 연료전지의 출력에 영향을 미치는 요인 중 사용자가 조절이 가능한 변수는 전류 인가에 따른 연료 소비량, 공급하는 연료의 유량, 전류값과 연료 투입량으로 결정되는 연료 이용률 등이 있으며, 다양한 작동조건에 따라 스택의 운전 온도, 출력이 결정된다. 현재는 이러한 조건의 변화를 일일이 실험을 통해 측정하여 시간적, 금전적 비용이 크게 발생하고 있다. 특히, 고온에서 작동하는 특성상 시동 및 정지 절차는 물론, 운전조건 변화에 따라서 성능이 변화하는 데에는 긴 안정화 시간이 필요하여 연료전지 성능이 예측된 값을 나타내는지 판단하고, 성능모델을 구축하는 데에도 많은 시간과 비용이 소요된다.
본 논문에서는 고체 산화물 연료전지 스택의 성능예측 모델을 구축함에 있어서, 다양한 조건의 실험에서 소요되는 시간과 비용을 저감할 수 있고, 동시에 신뢰도가 높은 모델을 구축할 목적으로 기계 학습(machine learning) 기법을 도입하여 모델을 구축하는 연구를 수행하였다. 다양한 기계 학습 기법 중 심층 신경망(deep learning) 기법은 학습 과정에서 내부적으로 비선형적인 연산을 여러 차례 수행하여 복잡하게 연관된 입력과 결과 간에서도 높은 예측 정확도를 보이는 기계 학습 방법이다. 심층 신경망의 세부 분류 중 하나인 합성곱 신경망(convolutional neural network) 기법은 생물 시신경의 작동 원리에서 착안된 방식으로9), 관측하는 대상의 세부적인 특징을 파악하는 필터의 개념을 도입해 분류의 성능이 뛰어나다. 착안점에서 알 수 있듯 시각적인 자료를 분류(classification)하는 것에 특화되어 개발되었으나, 연속적인 자료의 회귀(regression)에도 높은 예측 정밀도를 보이고 있다10).
본 논문에서는 기존에 수행한 SOFC 스택 실험 자료를 이용하여, 합성곱 신경망 방식으로 모델을 학습하여 예측값을 얻을 수 있었고, 이를 실험 결과와 비교하여 기계 학습 모델의 타당성을 검토하였다.
2. 고체산화물 연료전지 스택 실험
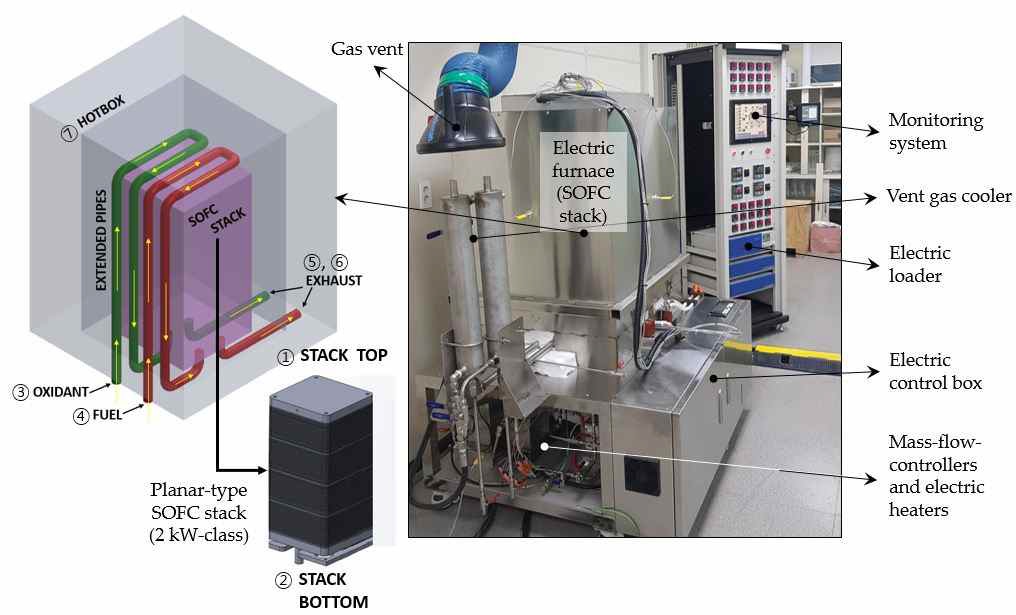
본 연구에서 사용된 SOFC 스택과 스택 평가 장치의 사진과 그림을 Fig. 1에 나타내었다. 본 실험에서는 ㈜ 미코(www.mico.kr)에서 제작한 2 kW 급 평판형 SOFC 스택을 활용하였다. 해당 스택은 연료극 지지형 평판형 셀을 사용하며, 전해질로는 yttria-stabilized zirconia (YSZ), 연료극은 nickel-YSZ (Ni-YSZ), 공기극은 lanthanum strontium cobalt ferrite (LSCF)를 사용한다8). SOFC 스택은 전기로(electric furnace) 내부에 설치하여 작동온도를 일정하게 유지하도록 하였고, 유량조절기(mass flow controller, MFC)와 전기히터(electric heater)를 이용하여 연료와 산화제를 실험조건에 맞도록 조정하였다. 연료로는 수소(H2)와 질소(N2)를 50:50으로 혼합한 가스를 사용하였고, 산화제로는 실험실에 공급되는 통상적인 고압공기를 이용하였다(일반적인 산업현장 수준으로 수분 제거). 연료전지 스택의 성능은 작동 온도에 따라 영향을 받는데, 스택의 성능을 대표하는 온도를 선정하기 위하여 스택의 상/하단, furnance의 수직 중간 높이, 산화제 및 연료의 입/출구 총 7가지 위치에서 온도를 계측하였다. 본 논문에서는 고체 산화물 연료전지의 작동 온도와 가스 입/출구의 온도차를 변경하면서 측정한 전류-전압 곡선(I-V curve) 실험 자료로 사용하였다. 전류-전압 곡선을 도출하는 데 적용한 실험조건을 정리하여 Table 1에 나타내었다.
전류-전압 곡선 도출실험은 가스공급량을 정격조건을 고정한 상태에서 인가전류를 증가시켜서 연료이용률을 변경하는 방식으로 진행하였다. 전류에 따른 전압 값은 전류를 증가시키면서 1차로 측정하고, 다시 전류를 감소시키면서 2차로 측정하였다. 전류 값 한 지점마다 안정화 시간을 5분으로 설정하였으며, 매 작동 온도에서 전류-전압 성능곡선을 얻기 위해 대략 300분(5시간) 가량의 시간이 소요되었다. 앞서 설명한 바와 같이 다양한 조건에서 성능자료를 확보하고, 이를 전기화학 모델 검증에 활용하기 위해서는 많은 실험시간이 소요된다. 이러한 장기간의 실험 시간 및 비용을 줄이기 위해 기계 학습(machine learnig)의 도입을 구상하였으며, 기존에 수행된 다양한 실험 자료를 활용하여 기계학습 기반의 성능모델을 개발하였다.
3. 심층 신경망을 이용한 성능 예측
3.1 자료 전처리
실험 자료를 활용하여 개발된 모델의 정확도와 학습 속도를 높이기 위하여 자료 전처리를 수행하였다. 측정된 여러 지점의 온도 중 스택에 직접적인 영향을 미치는 온도를 파악하고자 총 7지점(핫박스 내부, 스택 몸체 상/하부, 공기 입구/출구, 연료 입구/출구)로 선정하였으나, 7개의 온도를 모두 변수로 활용하여 모델을 학습시키기에는 학습에 활용할 실험 자료가 충분치 못하여, 이를 간략화 할 필요가 있다11,12).
본 연구에 사용된 SOFC는 여러 개의 셀이 적층된 형태이다. 연료전지가 작동하며 발생하는 열을 스택 상부와 측면으로 배출하는 구조이나 핫 박스로 인해 열이 원활히 배출되지 않아, 상부 및 측면부에 고온이 형성된다. 스택을 대표하는 작동 온도는 스택의 중앙부의 온도로 하는 것이 타당하다는 가정 하에 이를 추정하는 두 가지 방안을 도입하였다. 상기 설명한 7개 측정 온도를 단순 산술 평균한 온도를 평균 온도(average temperature, Taver), 연료와 유체의 유량을 고려하여 유입, 유출되는 유체의 평균 온도(입구와 출구의 평균)와 구조물에서 측정한 온도와 산술 평균을 낸 값을 대표 온도(representative temperature, Trept)로 정의하였다. Taver과 Trept을 구하는 식을 식 (1), 식 (2)에 정리하여 나타내었다.
| (1) |
| (2) |
다양한 종류의 입력을 받는 기계 학습 과정에서 자료 간의 규모가 크게 상이할 경우 가중치의 최적화 여부가 오차에 미치는 영향이 큰 것으로 알려져 있다10). 해당 실험에서도 온도는 700℃ 전후의 값으로 세 자리 숫자로 표시되는 반면, 전류 밀도는 0.5 mA/cm2에서 300 mA/cm2까지 변화하기 때문에, 제일 작은 값이 소수점 아래 값부터 세 자리 숫자까지 절대값이 큰 차이를 나타낸다. 따라서 각 입력 자료의 최대값을 1, 최소값을 0으로 설정하고, 입력 자료의 크기를 조정하는 정규화(normalization) 과정을 통해 온도와 전류 밀도 간의 규모를 대등한 수준으로 맞춰 주었다. 정규화에 사용된 방식은 식 (3)에 나타내었다.
| (3) |
위의 수식에서 x는 실제 입력 요소, xmin은 입력 값 중 최솟값, xmax는 입력 값 중 최댓값, xnorm은 정규화된 값이다.
3.2 일차원 합성곱 신경망을 통한 예측 및 검증
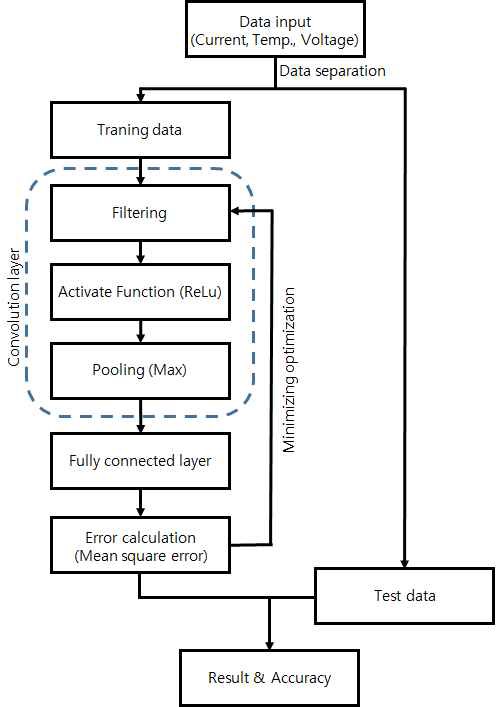
일차원 합성곱 신경망을 통한 학습 과정을 Fig. 2에 간략히 도시하였다. 합성곱 신경망은 합성곱 계층(convolutional layer), 활성화 함수(activate function), 풀링 계층(pooling layer)의 순차적인 계산으로 구성된다. 입력 자료를 합성곱 계층에서 filter라 불리는 가중치(weight)의 집단과 곱 연산을 수행한 뒤, 편향(bias)의 선형 합산을 통해 특징을 추출한다. 합성곱 연산이 수행된 자료는 활성화 함수를 적용하여 비선형적인 분류가 이뤄진다. 활성화를 위한 함수로는 Sigmoid 함수, Tanh 함수, Rectified linear unit (ReLU) 함수, Leaky ReLU 함수 등이 기존 연구에서 제안되었는데, 본 논문에서는 ReLU 함수를 사용하였다. ReLU 함수는 입력값이 0 이하일 경우 출력값 0으로 고정하며, 0 이상의 입력값을 받을 경우 입력값을 그대로 출력하는 함수이다. 풀링 계층은 합성곱과 활성화 함수로 분류된 자료의 크기를 조절하고, 특정 자료를 강조하는 역할을 수행한다. Max pooling을 적용하여 조절된 자료 중 가장 큰 값만을 출력하도록 설정하였다. 합성곱 연산 계층으로 추출한 특징을 결과와 동 차원으로 연산할 수 있도록 완전 연결 계층(fully-connected layer)을 통해 변환한 후에 예상 수치와 실제 실험의 수치 간의 오차를 계산한다.
이번 연구의 목적은 연속적인 값의 회귀이므로 오차는 평균 제곱 오차(mean square error)로 계산한다. 평균 제곱 오차를 최소화하는 방향으로 가중치(weight)와 편향(bias)을 조절하는 것이 회귀 학습의 최적화이다. 최적화에는 사용된 기법은 step의 방향(momentum)과 크기를 함께 고려하는 Adam을 사용하였다.
합성곱 신경망은 프로그래밍 언어 파이썬(Python) 환경에서 구글(Google, Mountain View, CA, USA) 사의 오픈 소스 기계 학습 라이브러리인 Tensorflow로 구현하였다. 또한, 구글 사의 브라우저 기반 개발 환경인 Colaboratory에서 수행하였다. 본 개발환경은 기계 학습 분야에서 일반적으로 널리 알려진 방법이므로 이에 관한 자세한 설명은 생략한다.
학습 자료와 검증에 사용될 자료는 Table 1에 제시된 5가지 조건의 실험 결과를 기반으로, 4가지 조건의 실험결과는 학습에 사용하고 나머지 한 조건의 실험 자료는 개발된 모델의 정확도 검증에 활용하는 지도 학습을 수행하였다(Cases 1-5).
기계 학습을 이용하여 전류-전압 성능을 예측한 결과는 Case로 표기하였는데, Cases 1-5의 숫자는 Table 1의 실험조건의 Case와 동일한 숫자를 사용한다. 예를 들어 결과 제시에서 Case 1은 Table 1의 Cases 2-5의 실험결과를 이용하여 기계학습 모델을 학습시키고, Table 1은 Case 1의 실험결과와 본 기계 학습 모델을 비교한 것을 의미한다. 동일하게, 결과값 Case 2는 Table 1의 Cases 1, 3-5의 네 가지 실험결과로 모델을 학습시키고, 실험 결과 Case 2와 모델을 비교한 결과이다.
기계 학습 모델이 예측하는 값과 비교할 수 있는 실제 실험/측정 자료가 존재하는 지도 학습이므로 정확도를 정량적으로 검증을 할 수 있다. 검증을 위해 평균 절대 백분율 오차(mean average percent error, MAPE), 평균 제곱근 편차(root mean square error, RMSE), 결정계수(coefficient of determination, [R2])를 사용하였다. 검증의 정밀도를 계산하는 공식은 식 (4)-(6)에 나타내었다.
| (4) |
| (5) |
| (6) |
위의 수식에서 y는 실제 계측 전압, 는 기계 학습을 통한 예상 전압, 는 전압의 평균이다.
4. 결과 및 고찰
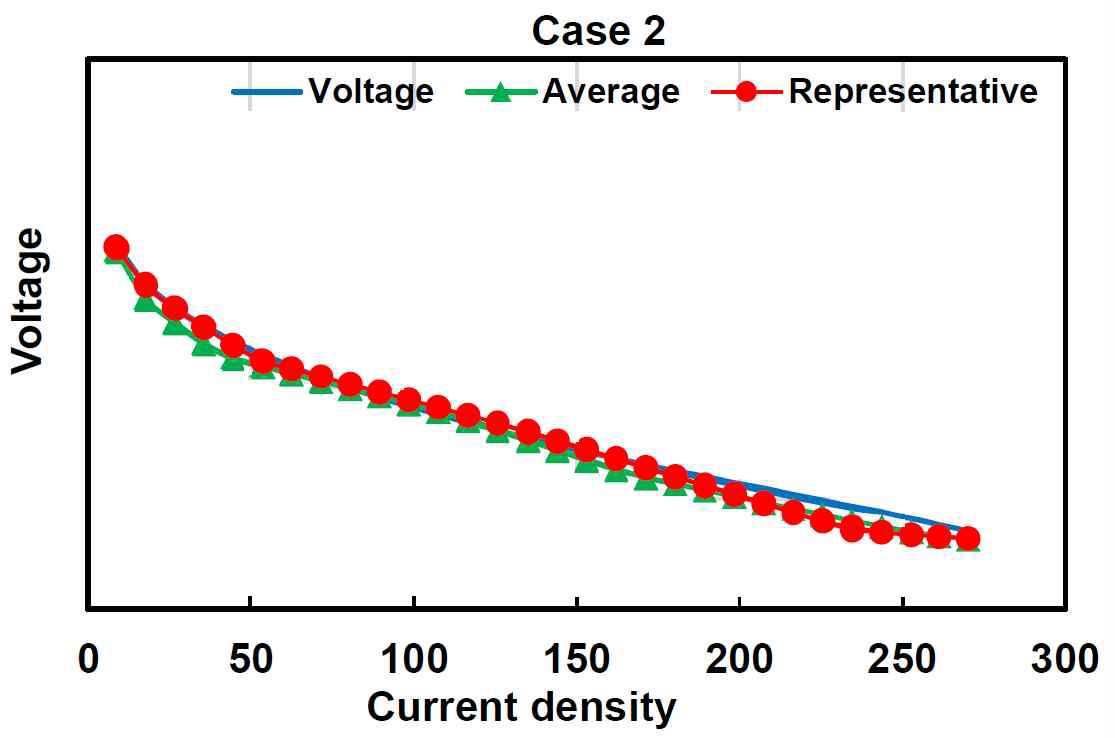
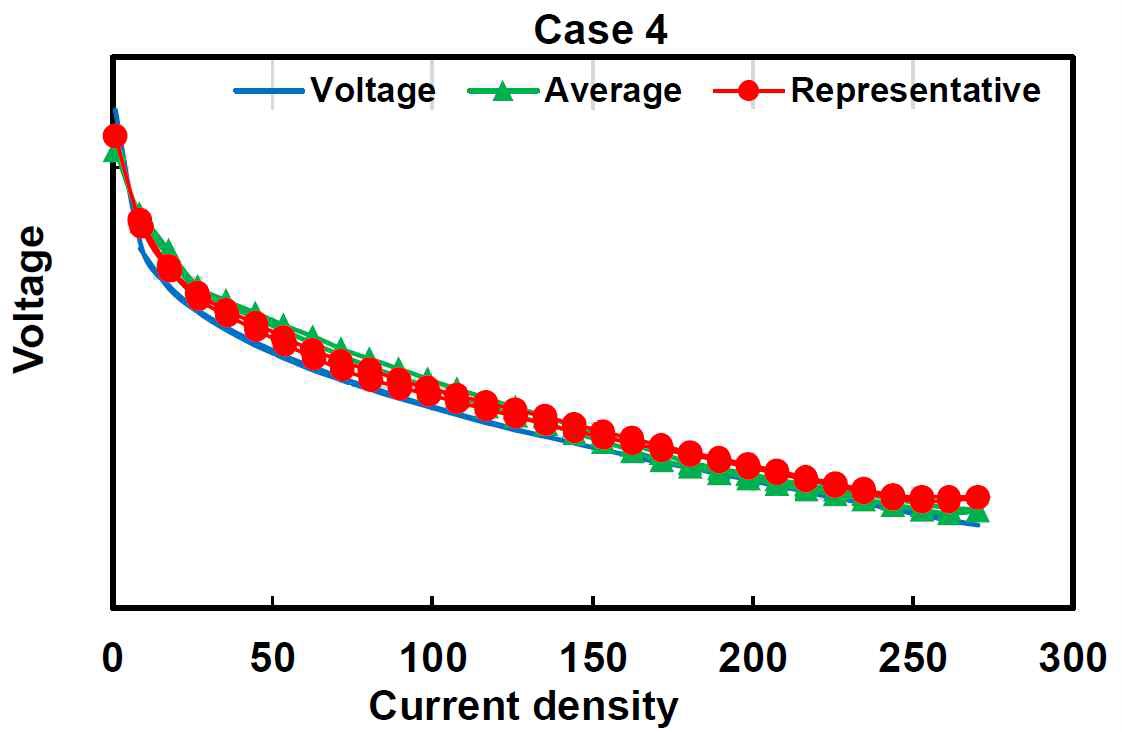
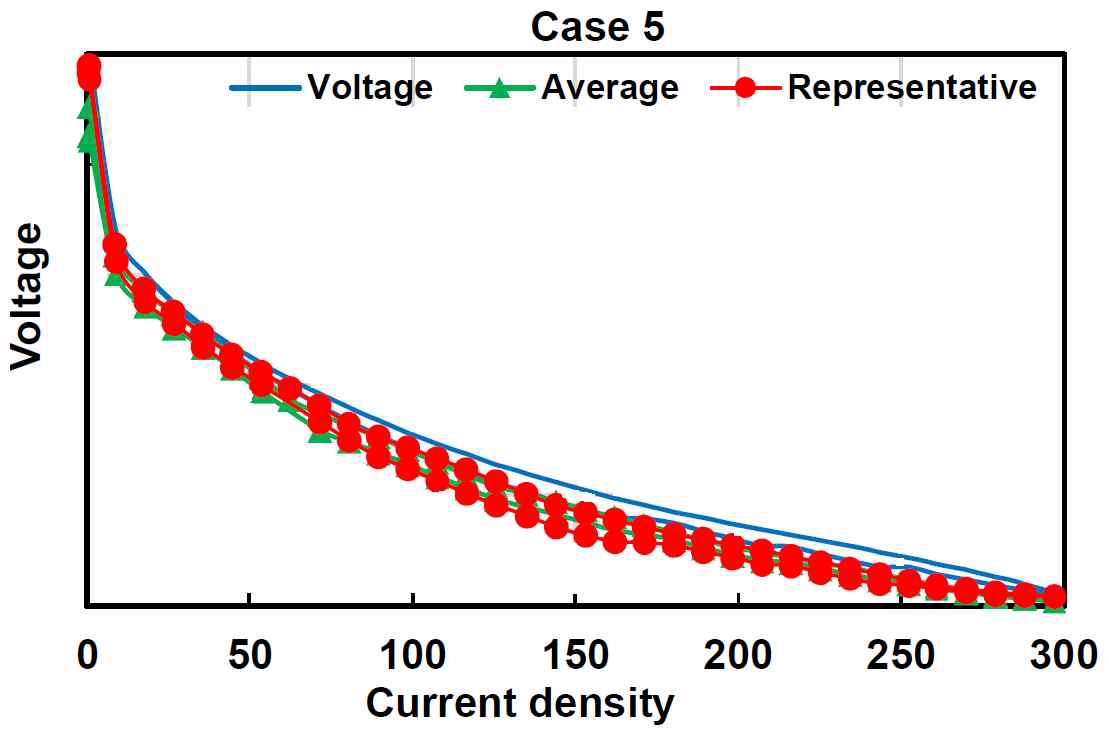
5차례의 측정 자료와 스택의 중간 부분을 추정하는 방법으로 앞서 제시한 평균 온도, 대표 온도 2가지를 조합하여 총 10가지의 기계 학습이 수행되었다. 기계 학습 도입의 목적인 실험에 소요되는 시간을 절감할 수 있다는 측면에서 의미 있는 결과를 얻을 수 있었다. 앞서 언급한 바와 같이 하나의 선도를 그리기 위해 실험에서는 300분 안팎의 시간이 소요되었으나, 기계 학습이 학습을 통해 모델을 도출하는 데 소요된 시간은 21초이다. 기계 학습을 통한 전압의 예측 값이 실험 자료와 얼마나 정성적으로 일치하는지 보기 위해 전류 밀도-전압 선도를 Fig. 3에서부터 Fig. 7까지 도시하였다.
각 선도의 파란 선은 실험을 통해 얻은 자료이며, 빨간 원은 대표 온도를 이용한 기계 학습 추정값, 초록 삼각형은 평균 온도를 이용한 기계 학습 추정값이다. 선도에서 전압의 값은 연료전지 제조사의 기술 보안을 위해 의도적으로 생략하였다.
입력으로 사용한 온도 및 전류 밀도로 추정한 전압을 식 (4)-(6)을 이용하여 정량적으로 검증한 결과를 Table 2에서부터 Table 6에 정리하였다. 그 결과, 평균 절대 백분율 오차는 내삽의 영역에서 0.4702-0.8782%, 외삽의 영역에서 1.4572-1.9402%로 계산되었다. 이는 기계 학습으로 예측한 전압은 내삽의 영역에서는 1% 미만, 외삽의 영역에서도 2% 미만의 오차를 기대할 수 있음을 의미한다. 오차와 편차의 비율을 나타내는 결정계수 또한 내삽의 영역에서는 최소 0.9257, 외삽의 영역에서는 0.8114로 기계 학습으로 생성한 모델이 정확도가 높으면서도 편차도 작아 실제 전압을 충분히 잘 모사함을 보인다. 대표 온도를 변수로 사용하여 학습한 경우가 모델의 정확도가 전반적으로 높게 계산되었는데, 이는 연료전지 연료 및 공기의 입구, 출구로 드나드는 유량의 물리적 정보를 포함하기 때문에 연료전지 스택의 온도를 대표하기에 더욱 정확한 값이라 할 수 있다. 이러한 사항은 기계 학습이 전체적인 자료를 잘 모사하는 가중치와 편향의 값을 빠르게 찾아내어 수렴하는 것으로부터도 추정할 수 있다. 즉, 적합한 물리적인 현상을 반영하여 자료를 전처리하면 기계 학습의 성능이 향상된다. Cases 4와 5에서는 다른 Case보다 기계 학습을 통한 예측 정확도가 떨어지는 경향이 나타났는데, Case 4는 전체 Case 중 가장 고온 운전 조건이며, Case 5는 가장 저온 운전 조건에서 수행된 실험이다. Cases 1-3은 연료전지 스택 실험에서 최고온과 최저온의 결과를 포함하여 학습을 수행한 뒤, 학습 구간의 사이에 있는 조건을 예측하는 반면, Cases 4와 5는 학습에 사용한 결과의 바깥 영역의 값을 하므로 오차가상대적으로 크게 나타났다. 즉, 기계 학습으로 성능을 예측하는 과정은 내삽(interpolation)의 영역을 예상하는 것이 외삽(extrapolation)의 영역을 예상하는 것보다 정확도가 높음을 유추할 수 있다. 이는 기계 학습을 병행하는 성능 실험에서 기기의 한계 조건의 실험을 먼저 수행하여 구간 내에 있는 값을 예측하는 것이 더욱 효율적임을 시사한다.
5. 결 론
본 논문에서는 고체 산화물 연료전지의 성능 측정과 모델 개발에 소요되는 시간을 줄이면서도 높은 수준의 모델 예측 정확도를 확보하기 위한 방안으로 기계 학습을 도입하였다. 사전에 수행된 실험 자료를 기반으로 1차원 합성곱 신경망 기반의 기계 학습을 수행하였고, 실제 측정 자료와 학습으로 추정된 자료의 정성적, 정량적인 검증을 통해 기계 학습을 통한 진단의 타당성을 확보하였다. 기계 학습으로 생성한 전압 예측 모델은 내삽의 자료는 1% 미만, 외삽의 자료는 2% 미만의 오차라는 충분히 신뢰할 수 있는 결과를 보였다. 또한, 다양한 작동 조건에 대하여 기계학을 통해 연료전지 성능 예측모델을 개발한 사항을 정리하여 다음과 같은 결론을 도출하였다.
1) 물리적인 현상을 반영할 수 있도록 자료를 적절하게 전처리하는 것으로 기계 학습의 예측 정확도를 높일 수 있다.
2) 기계 학습으로 인한 성능 추정은 보간의 영역을 유추하는 것이 외삽의 영역을 유추하는 것보다 정밀도가 높다.
기계 학습은 학습 자료의 양이 많아질수록 예측 정확도가 높아진다는 사실은 자명하다. 본 논문에서 사용된 학습 자료를 더욱 늘린다면 성능 예측 정확도가 더욱 높아질 것이며, 물리적 현상의 반영이 모델 성능에 미치는 영향을 정량적으로 분석 할 수 있을 것이다. 이에 연구실은 실시간으로 연료전지의 측정 자료를 초 단위로 입력받아 성능을 모사하는 실험 장치 및 모델 개발을 진행하고 있다.
Acknowledgments
본 연구는 산업통상자원부 한국산업기술평가관리원 산하 산업기술혁신사업(10082569, 5 kW 급 상용고효율 연료전지-엔진 하이브리드 시스템 설계 패키지 및 시제품 개발)의 연구비 지원으로 수행되었습니다.
References
-
T. S. Park, T. H. Nam, D. G. Lee, S. K. Lee, and J. S. Moon, “A study of deduction of evaluation items for design of SOFC stack safety performance evaluation system”, J. Korean Inst. Gas., Vol. 21, No. 6, 2017, pp. 81-87.
[https://doi.org/10.7842/kigas.2017.21.6.81]

-
F. Ramadhani, M. A. Hussain, H. Mokhlis, and S. Hajimolana, “Optimization strategies for solid oxide fuel cell (SOFC) application: a literature survey”, Renewable Sustainable Energy Rev., Vol. 76, 2017, pp. 460-484.
[https://doi.org/10.1016/j.rser.2017.03.052]

-
A. Kirubakaran, S. Jain, and R. K. Nema, “A review on fuel cell technologies and power electronic interface”, Renewable Sustainable Energy Rev., Vol. 13, No. 9, pp. 2430-2440.
[https://doi.org/10.1016/j.rser.2009.04.004]

-
M. C. Williams, S. D. Vora, and G. J. Gary, “Worldwide status of solid oxide fuel cell technology” ECS Transactions, Vol. 96, No.1, 2020, pp. 1-10.
[https://doi.org/10.1149/09601.0001ecst]

-
M. Yoda, S. Inoue, Y. Takuwa, K. Yasuhara, and M. Suzuki, “Development and commercialization of new residential SOFC CHP system”, ECS transactions, Vol. 78, No.1, 2017, pp. 125-132.
[https://doi.org/10.1149/07801.0125ecst]

-
W. M. Chen and H. N. Kim, “Energy, economic, and social impacts of a clean energy economic policy: fuel cells deployment in Delaware”, Energy Policy, Vol. 144, 2020, pp. 111617.
[https://doi.org/10.1016/j.enpol.2020.111617]

-
M. Noponen, P. Torri, J. Göös, J. Puranen, H. Kaar, S. Pylypko, and E. Õunpuu, “Elcogen–next generation solid oxide cell and stack technology”, ECS Transactions, Vol. 91, No. 1, 2019, pp. 91-97.
[https://doi.org/10.1149/09101.0091ecst]

-
Y. S. Kim, Y. D. Lee, and K. Y. Ahn, “System integration and proof-of-concept test results of SOFC–engine hybrid power generation system”, Applied Energy, Vol. 277, 2020, 115542.
[https://doi.org/10.1016/j.apenergy.2020.115542]

-
S. Malek, F. Melgani, and Y. Bazi, “One‐dimensional convolutional neural networks for spectroscopic signal regression”, J. Chemom., Vol. 32, No. 5, 2018, pp. e2977.
[https://doi.org/10.1002/cem.2977]

-
J. M. Jo, “Effectiveness of normalization pre-processing of big data to the machine learning performance”, The Journal of the Korea Institute of Electronic Communication Sciences, Vol. 14, No. 3, 2019, pp. 547-552.
[https://doi.org/10.13067/JKIECS.2019.14.3.547]

-
R. Ma, T. Yang, E. Breaz, Z. Li, P. Briois, and F. Gao, “Data-driven proton exchange membrane fuel cell degradation predication through deep learning method”, Applied Energy, Vol. 231, 2018, pp. 102-115.
[https://doi.org/10.1016/j.apenergy.2018.09.111]

-
Y. H. Jang, J. Y. Kim, and S. K. Oh, “A study on information data segmentation method using optimization algorithm”, Journal of Korean Institute of Intelligent Systems, Vol. 28, No. 4, 2018, pp. 321-327.
[https://doi.org/10.5391/JKIIS.2018.28.4.321]