저등급 열원으로 구동되는 직렬 열병합 발전시스템의 엑서지와 엔트랜시 성능 특성
2020 The Korean Hydrogen and New Energy Society. All rights reserved.
Abstract
In this paper, entransy analysis is carried out for combined heat and power (CHP) generation system driven by low-grade heat source compared with energy and exergy analyses. The system consists of a regenerative organic rankine cycle (ORC) and an additional process heater in a series circuit. Special attention is paid to the effects of the turbine inlet pressure, source temperature, and the working fluid on the thermodynamic performance of the system. Results showed that the work efficiency of entransy is higher than that of energy but lower than that of exergy, wheress the process heat efficiency of entransy is lower than that of energy but higher than that of exergy. Entrance analysis showed the potential to complement the exergy analysis in the optimal design of the energy system.
Keywords:
Combined heat and power (CHP), Organic rankine cycle (ORC), Low-grade heat source, Exergy, Entransy키워드:
열병합, 유기 랭킨 사이클, 저등급 열원, 엑서지, 엔트랜시1. 서 론
저등급 열원으로부터 전기와 같이 보다 가치 있는 에너지 형태로 에너지를 변환하는 방법으로서 유기 랭킨 사이클(organic rankine cycle, ORC)은 가장 경쟁력 있는 시스템 중 하나로 평가되어 왔다1,2). 에너지 변환효율을 최대한 높이기 위한 연구가 광범위하게 진행되어 왔지만, 저등급 열원을 사용하는 한 효율은 카르노 정리에 따라 한계에 부딪힐 수밖에 없어 경제성을 확보하기 쉽지 않고 환경문제 등 아직 많은 문제점이 남아 있다3).
저등급 열원을 이용한 에너지 변환 시스템의 경제성을 획기적으로 높이는 방법 중 하나가 ORC 기반의 열병합 발전 시스템이다4,5). 열병합 발전은 한 공정에서 기계와 열 에너지를 동시에 생산하는 것으로서 에너지 효율을 획기적으로 높일 수 있는 입증된 방법이다6). 열병합 발전의 개념은 오래되었지만 ORC에 기반한 열병합 발전 기술은 성숙하지 못하여 10 kWe 이하의 전력 규모에 초점을 맞춘 사례가 아직은 시장에 거의 없는 실정이다7,8).
바이오매스9), 시멘트 공장의 폐열10), 지열원11) 등을 이용한 ORC 기반 열병합 발전 시스템에 관한 연구가 보고되었다. Pereira 등12)은 ORC 기반 마이크로 열병합 발전 시스템에서 증발기 설계 방법을 제시하였으며, Arabkoohsara와 Nami13)는 폐열을 이용한 ORC 기반 열병합 발전 시스템에서 전기 생산의 비중을 극대화하기 위한 연구를 수행하였다. Sachdeva와 Singh14)은 브레이튼 사이클, 증기 랭킨 사이클, ORC의 삼중 결합 사이클을 연구하였으며 Kim 등15), Kim16)은 병렬과 직렬 연결 ORC 기반 열병합 발전의 열역학적 성능 특성에 대해 연구하였다.
최근 들어 축전기의 전기 포텐셜에 대한 열전달의 상사 개념으로 엔트랜시(entransy)가 제안되었다17). 엔트랜시는 열전달 과정 중에 소산되며, 엔트랜시 소산(dissipation)은 열전달에 있어서 비가역성의 또 다른 척도가 된다18-21). 엔트랜시는 열역학 상태량이며 열역학 제2법칙을 다른 방식으로 설명하기 위해 사용될 수 있다. 열 엔트랜시와 일 엔트랜시는 각각 열과 일의 상호작용을 통해 정의된다22,23).
Kim과 Kim24), Han과 Kim25)은 카르노 사이클의 최적화를 위한 엔트랜시 성능 특성에 대해 연구하였으며, Wang 등26)은 저등급 열원으로 구동되고 혼합물질을 작동유체로 사용하는 ORC의 엔트로피와 엔트랜시 성능 특성에 대해 연구하였다.
본 연구에서는 저등급 열원으로 구동되는 ORC 기반 직렬연결 열병합 발전시스템의 엔트랜시 성능 특성을 에너지 및 엑서지와 비교해서 해석한다. 여덟 가지 작동유체를 대상으로 열원온도와 터빈입구압력의 변화가 시스템의 성능에 미치는 영향을 분석한다.
2. 시스템 해석
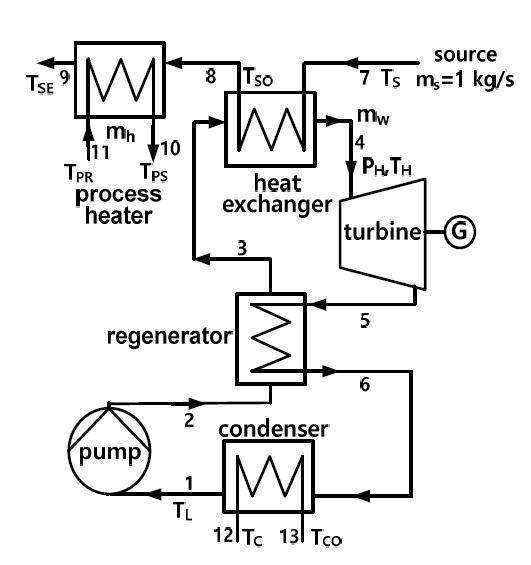
본 논문에서는 Fig. 1에서 보는 바와 같이 저온 열원으로 구동되어 전기를 생산하는 ORC와 공정열이 병렬로 연결된 열병합 시스템을 고려한다. 본 연구에서 기본적인 가정은 다음과 같다11,15,16): 1) 터빈 입구 압력은 작동유체의 임계압력보다 낮은 아임계 사이클이다. 2) 터빈 입구에서 작동유체는 순수 증기 상태이다. 3) 시스템에서 열교환기를 제외한 열손실은 무시한다. 4) 터빈과 펌프 이외에서의 압력 변화는 무시한다. 5) 공정열은 75℃로 공급해서 50℃로 회수한다. 6) 펌프와 터빈에서의 등엔트로피 효율은 각각 ηp와 ηt로 일정하다. 7) 열교환기에서는 고온과 저온 유체의 최소 온도차는 미리 설정한 핀치 포인트와 같다. 엑서지 X와 엔트랜시 G는 다음과 같이 정의한다24,25).
| (1) |
| (2) |
여기에서 T0는 기준 온도인 사장상태 온도이고 H와 S는 각각 엔탈피와 엔트로피이며 사장상태를 기준으로 한다.
열원 에너지 Es, 일 에너지 Ew, 공정열 에너지 Ep, 유용 에너지 Et는 다음과 같이 정의한다
| (3) |
| (4) |
| (5) |
| (6) |
열원 엑서지 Xs, 일 엑서지 Xw, 공정열 엑서지 Xp, 유용 엑서지 Xt는 다음과 같이 정의한다.
| (7) |
| (8) |
| (9) |
열원 엔트랜시 Es, 일 엔트랜시 Ew, 공정열 엔트랜시 Ep, 유용 엔트랜시 Et는 다음과 같이 정의한다24,25).
| (10) |
| (11) |
| (12) |
| (13) |
본 논문에서 에너지, 엑서지 및 엔트랜시에 대한 일 효율 EWE, EWX 및 EWG는 열원의 물리량에 대한 일 물리량의 비로 각각 정의하며, 공정열 효율 EPE, EPX 및 EPG는 열원의 물리량에 대한 공정열 물리량의 비로 각각 정의되고, 총효율 ETE, ETX 및 ETG는 열원 물리량에 대한 일물리량과 열물리량을 합한 총 물리량의 비로 각각 정의되며 Table 1에 정리되어 있다.
ORC의 작동유체로 R134a와 R123을 고려하며 작동유체의 분자량 M, 임계온도 Tcr, 임계압력 Pcr, Global warming potential (GWP), Ozone depletion potential (ODP) 등 기본적인 데이터들은 Table 2에서 보여준다. 본 논문에서 ORC의 작동유체는 R134a, R152a, R290, R600a, R600, R245fa, R123 그리고 R601a의 여덟 가지를 고려하며, 작동유체의 열역학 상태량은 Patel-Teja 방정식을 이용하여 계산하였다27,28).
3. 결과 및 고찰
본 연구에서 열원 유체는 1 kg/s의 표준 공기로 가정하며 시뮬레이션을 위한 기본적인 시스템 데이터는 다음과 같다24,25): 열원 온도 TS=200℃, 응축 온도 TL=35℃, 냉각수 온도 TC=25℃, 핀치 포인트 온도차 ΔTpp=8℃, 터빈입구압력 PH=25 bar, 펌프 효율 ηp=0.8, 터빈 효율 ηt=0.819) 그리고 열원 온도 TS는 150℃부터 300℃까지, 터빈입구 압력 PH2는 10 bar부터 40 bar까지 고려하며, 터빈입구 온도 TH는 열원온도와 15℃ 낮다고 설정한다.
Fig. 2에서는 터빈입구압력 및 작동유체의 변화가 (a) 에너지, (b) 엑서지 및 (c) 엔트랜시의 일효율에 미치는 영향을 보여준다. 전체 작동유체, 전 범위의 열원온도에서 일효율은 엔트랜시 효율 EWG가 에너지 효율 EWE보다는 높고 엑서지 효율 EWX보다는 낮아서, 일효율은 엑서지, 엔트랜시 그리고 에너지 순으로 높다. 터빈입구압력이 증가함에 따라 임계온도가 낮은 편인 R134a, R152a 및 R290의 경우에는 단조 증가하나, 나머지 임계온도가 높은 편인 R600a, R600, R245fa, R123 및 R601a의 경우에는 증가 및 감소하다 다시 증가하여 극대값과 극소값을 갖는다. 압력이 증가함에 따라 에너지와 엑서지 효율이 최대가 되는 작동유체는 R123, R600, R600a, R290, R152a 등으로 변하며 최소가 되는 작동유체는 R601a이다. 압력이 증가함에 따라 엔트랜시 효율이 최대가 되는 작동유체는 R123, R600, R152a 등으로 변하며 최소가 되는 작동유체는 R245fa에서 R601a로 변한다.
Fig. 3에서는 터빈입구압력 및 작동유체의 변화가 (a) 에너지, (b) 엑서지 및 (c) 엔트랜시의 공정열 효율에 미치는 영향을 보여준다. 전체 작동유체, 전 범위의 터빈입구압력에서 공정열 효율은 일효율의 경우와는 반대로 엔트랜시 효율 EPG가 에너지 효율 EPE보다는 낮고 엑서지 효율 EPX보다는 높아서, 공정열 효율은 에너지, 엔트랜시 그리고 엑서지 순으로 높다. 또한 에너지, 엑서지 및 엔트랜시 공정열 효율은 모든 작동유체의 경우에 터빈입구압력이 증가함에 따라 증가하다 감소하여 극대값을 갖는다. 그리고 공정열 효율은 에너지, 엑서지 및 엔트랜시 모두 R134a와 R152a의 경우만 순서가 바뀌고 나머지는 모두 동일 압력 조건에서 작동유체의 임계온도가 높을수록 높아져 R601의 경우가 가장 효율이 높고 R152a의 경우가 가장 효율이 낮다.
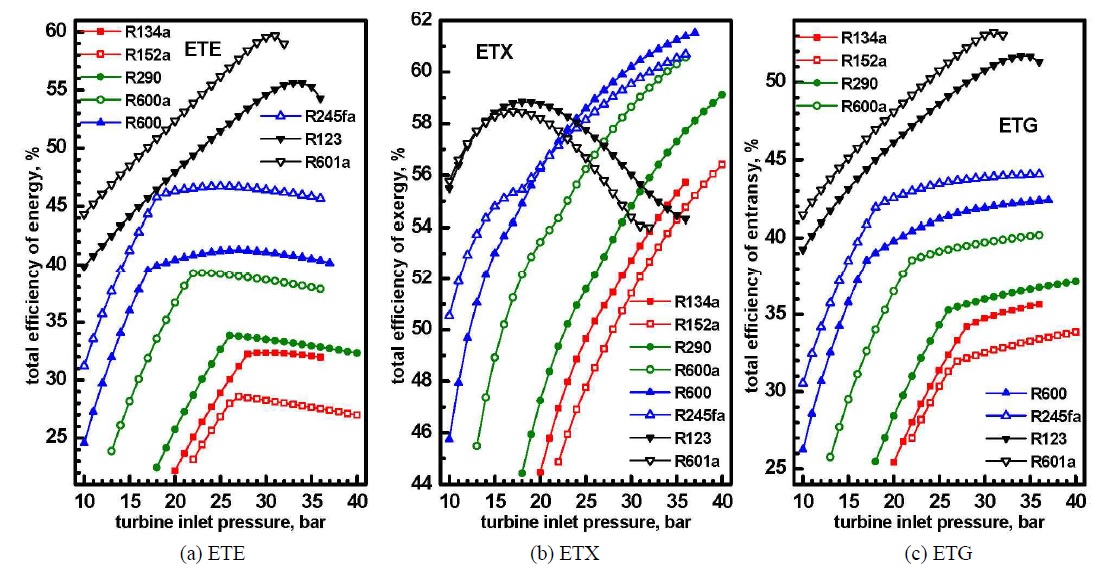
Fig. 4에서는 터빈입구압력 및 작동유체의 변화가 (a) 에너지, (b) 엑서지 및 (c) 엔트랜시의 총효율에 미치는 영향을 보여준다. 총효율은 일효율과 공정열 효율의 합으로 정의되는데, 일효율은 엑서지, 엔트랜시, 에너지 순으로 높고 공정열 효율은 반대로 에너지, 엔트랜시, 엑서지 순으로 높기 때문에 크기 관계가 복잡하다. 엔트랜시 총효율 ETG는 임계온도가 상대적으로 낮은 R134a, R152a, R290, R600a 및 R600의 경우에는 에너지 총효율 ETE보다 더 높지만 임계온도가 상대적으로 높은 R245fa, R123 및 R601a의 경우에는 더 낮다. 엑서지 총효율 ETX는 R123과 R601a를 제외하고는 에너지나 엔트랜시 총효율보다 높다. 그러나 작동유체가 R245fa와 R601a의 경우에 엑서지 총효율은 터빈입구압력이 낮은 범위에서는 에너지 총효율보다 높지만 터빈입구압력이 높은 영역에서는 더 낮다. 또한 터빈입구압력이 증가함에 따라 에너지 총효율은 증가하다 감소하여 극대값을 갖지만 엔트랜시와 엑서지 총효율은 R123과 R601a의 경우에는 극대값을 갖지만 그 외에는 터빈입구압력이 높아짐에 따라 단조 증가한다.
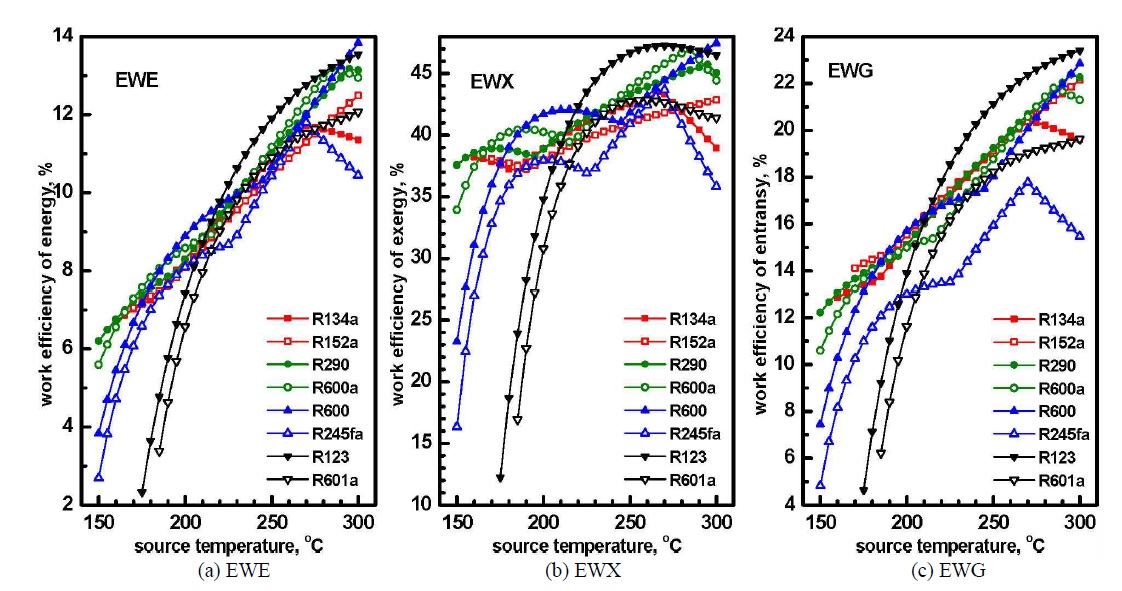
Fig. 5에서는 열원온도 및 작동유체의 변화가 (a) 에너지, (b) 엑서지 및 (c) 엔트랜시의 일효율에 미치는 영향을 보여준다. 전체 작동유체, 전 범위의 열원온도에서 일효율은 엔트랜시 효율 EWG가 에너지 효율 EWE보다는 높고 엑서지 효율 EWX보다는 낮아서, 일효율은 엑서지, 엔트랜시 그리고 에너지 순으로 높다. 열원온도가 증가함에 따라 에너지와 엔트랜시 일효율은 작동유체가 R152a, R600, R123 및 R601a인 경우에는 단조 증가하고 R134a, R290, R600a 및 R600의 경우에는 극대값을 갖는다. 이에 비해 엑서지 일효율의 경우에는 거동 특성이 더 복잡하고 R134a, R290, R600a, R600 및 R245fa의 경우에는 열원온도에 대해 두 개 이상의 극값을 갖는다. 또한 에너지, 엑서지 및 엔트랜시 일효율이 최대가 되는 작동유체는 열원온도가 증가함에 따라 R290, R600a, R600, R123 등으로 변한다.
Fig. 6에서는 열원온도 및 작동유체의 변화가 (a) 에너지, (b) 엑서지 및 (c) 엔트랜시의 공정열 효율에 미치는 영향을 보여준다. 전체 작동유체, 전 범위의 열원온도에서 공정열 효율은 에너지, 엔트랜시 그리고 엑서지 순으로 높다. 또한 에너지, 엑서지 및 엔트랜시의 공정열 효율은 열원온도가 증가함에 따라 작동유체에 따라 단조 감소, 극대값, 극소값, 극대값과 극소값, 극소값-극대값-극소값 등 다양한 거동을 보인다. 에너지, 엑서지 및 엔트랜시의 공정열 효율이 최대가 되는 작동유체는 임계온도가 높은 R601a, R123, R245fa 및 R600 등이고 최소가 되는 작동유체는 R152a이다.
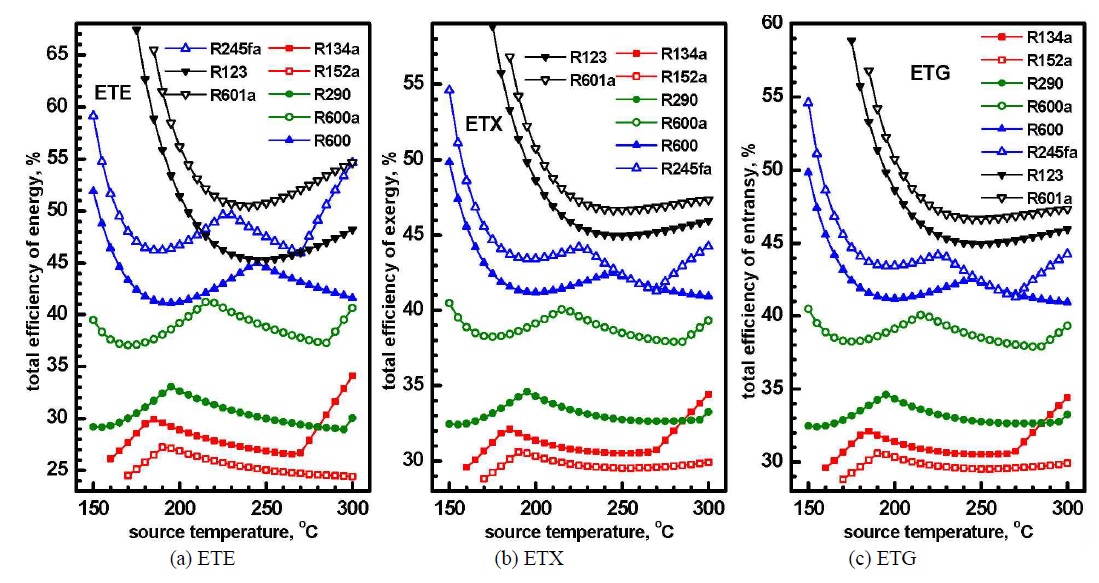
Fig. 7에서는 열원온도와 작동유체의 변화가 (a) 에너지, (b) 엑서지 및 (c) 엔트랜시의 총효율에 미치는 영향을 보여준다. 열원온도 변화에 따른 에너지, 엑서지 및 엔트랜시의 총효율도 일효율은 엑서지, 엔트랜시, 에너지 순으로 높고 공정열 효율은 반대로 에너지, 엔트랜시, 엑서지 순으로 높기 때문에 거동이 복잡하다. 총효율의 거동은 대체적으로 작동유체의 임계온도가 낮은 경우에 극대-극소값을 갖다가 임계온도가 높아짐에 따라 극값에 상응하는 열원온도가 높아지면서 극소-극대-극소값, 극소-극대값, 극소값 등으로 변화한다. 에너지, 엑서지 및 엔트랜시의 총효율은 작동유체가 R601의 경우에 최대가 되고 R152a의 경우에 최소가 된다.
4. 결 론
본 논문에서는 저등급 열원으로 구동되는 ORC 기반 직렬연결 열병합 발전 시스템의 에너지, 엑서지 및 엔트랜시 성능을 비교 해석하였다. 일효율, 공정열효율 및 총효율을 터빈입구압력, 열원온도 및 작동유체의 변화에 따른 영향을 분석하였다. 주요 결과는 다음과 같다.
1) 에너지, 엑서지 및 엔트랜시 효율 특성은 터빈입구압력, 열원온도 및 작동유체의 변화에 따라 큰 영향을 받는다.
2) 모든 해석 범위에서 엔트랜시 일효율은 에너지 경우보다 높고 엑서지 경우보다 낮으며, 엔트랜시 공정열 효율은 반대로 에너지 경우보다 낮고 엑서지 경우보다 높다.
3) 일효율과 공정열 효율의 합으로 정의되는 총효율은 터빈입구압력, 열원온도 및 작동유체에 따라 거동 특성이 복잡하게 변화하고, 엑서지 및 엔트랜시 효율간 크기 순서도 달라지며, 최고 효율과 최저 효율을 보이는 작동유체도 달라진다.
4) 에너지 시스템의 최적설계에 있어서 엔트랜시 해석은 에너지와 엑서지 해석을 보완할 수 있는 잠재성이 있다.
Acknowledgments
이 논문은 2018년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업입니다(NRF-2018R1D1A1B07048866).
References
-
A. Schuster, S. Karellas, E. Kakaras, and H. Spliethoff, “Energetic and economic investigation of organic Rankine cycle applications”, Appl. Therm. Eng., Vol. 29, No. 8-9, 2009, pp. 1809-1817.
[https://doi.org/10.1016/j.applthermaleng.2008.08.016]

-
T. C. Hung, S. K. Wang, C. H. Kuo, B. S. Pei, and K. F. Tsai, “A study of organic working fluids on system efficiency of an ORC using low-grade energy sources”, Energy, Vol. 35, No. 3, 2010, pp. 1403-1411.
[https://doi.org/10.1016/j.energy.2009.11.025]

-
M. Aguirre and G. Ibikunle, “Determinants of renewable energy growth: a global sample analysis”, Energy Policy, Vol. 69, 2014, pp. 374-384.
[https://doi.org/10.1016/j.enpol.2014.02.036]

-
K. H. Kim and H. Perez-Blanco, “Performance analysis of a combined organic Rankine cycle and vapor compression cycle for power and refrigeration cogeneration”, Appl. Therm. Eng., Vol. 91, 2015, pp. 964-974.
[https://doi.org/10.1016/j.applthermaleng.2015.04.062]

-
K. H. Kim and K. C. Kim, “Thermodynamic performance analysis of a combined power cycle using low grade heat source and LNG cold energy”, Appl. Therm. Eng., Vol. 70, No. 1, 2014, pp. 50-60.
[https://doi.org/10.1016/j.applthermaleng.2014.04.064]

-
G. Qiu, “Selection of working fluids for micro-CHP systems with ORC”, Renewable Energy, Vol. 48, 2012, pp. 565-570.
[https://doi.org/10.1016/j.renene.2012.06.006]

-
J. S. Pereira, J. B. Ribeiro, R. Mendes, G. C. Vaz, and J. C. André, “ORC based micro-cogeneration systems for residential application - a state of the art review and current challenges”, Renew. Sustain. Energy Rev., Vol. 92, 2018, pp. 728-743.
[https://doi.org/10.1016/j.rser.2018.04.039]

-
M. Santos, J. André, E. Costa, R. Mendes, and J. Ribeiro, “Design strategy for component and working fluid selection in a domestic micro-CHP ORC boiler”, Appl. Therm. Eng. Vol. 169, 2020, pp. 114945.
[https://doi.org/10.1016/j.applthermaleng.2020.114945]

-
U. Dresher and D. Brueggemann, “Fluid selection for the organic Rankine cycle (ORC) in biomass power and heat plants”, App. Therm. Eng,, Vol. 27, No. 1, 2007, pp. 223-228.
[https://doi.org/10.1016/j.applthermaleng.2006.04.024]

-
J. Wang, Y. Dai, and L. Gao, “Exergy analysis and parametric optimization for different cogeneration power plants in cement industry”, App. Energy, Vol. 86, 2009, pp. 941-948.
[https://doi.org/10.1016/j.apenergy.2008.09.001]

-
F. Heberle and D. Brueggemann, “Exergy based fluid selection for a geothermal organic Rankine cycle for combined heat and power generation”, Appl. Therm. Eng., Vol. 30, No. 11-12, 2010, pp. 1326-1332.
[https://doi.org/10.1016/j.applthermaleng.2010.02.012]

-
J. S. Pereira, J. B. Ribeiro, R. Mendes, and J. C. André, “Analysis of a hybrid (topping/bottoming) ORC based CHP configuration integrating a new evaporator design concept for residential applications”, Appl. Therm. Eng., Vol. 160, 2019, pp. 113984.
[https://doi.org/10.1016/j.applthermaleng.2019.113984]

-
A. Arabkoohsara and H. Nami, “Thermodynamic and economic analyses of a hybrid waste-driven CHP–ORC plant with exhaust heat recovery”, Energy Convers. Mgmt., Vol. 187, 2019, pp. 512-522.
[https://doi.org/10.1016/j.enconman.2019.03.027]

-
J. Sachdeva and O. Singh, “Comparative evaluation of solarized triple combined cycle for different ORC fluids”, Renewable Energy, Vol. 163, 2021, pp. 1333-1342.
[https://doi.org/10.1016/j.renene.2020.09.063]

-
K. H. Kim, B. D. Park, and M. H. Kim, “Thermodynamic performance analysis of a cogeneration system in series circuit using regenerative ORC”, Trans Korean Hydrogen New Energy Soc, Vol. 26, No. 3, 2015, pp. 278-286.
[https://doi.org/10.7316/KHNES.2015.26.3.278]

-
K. H. Kim, “Theoretical characteristics of thermodynamic performance of combined heat and power generation with parallel circuit using organic Rankine cycle”, J. Korean Solar Energy Society, Vol. 31, No. 6, 2011, pp. 49-56.
[https://doi.org/10.7836/kses.2011.31.6.049]

-
Z. Y. Guo, H. Y. Zhu, and X. G. Liang, “Entransy—a physical quantity describing heat transfer ability”, Int. J. Heat Mass Transfer, Vol. 50, No. 13-14, 2007, pp. 2545-2556.
[https://doi.org/10.1016/j.ijheatmasstransfer.2006.11.034]

-
X. T. Cheng, X. G. Liang, and Z. Y. Guo, “Entransy decrease principle of heat transfer in an isolated system”, Chin. Sci. Bull., Vol. 56, 2011, pp. 847-854.
[https://doi.org/10.1007/s11434-010-4328-4]

-
X. T. Cheng and X. G. Liang, “From thermomass to entransy”, Int. J. Heat Mass Transfer, Vol. 62, 2013, pp. 174-177.
[https://doi.org/10.1016/j.ijheatmasstransfer.2013.02.063]

-
Z. Q. Yu, P. Wang, W. J. Zhou, Z. Y. Li, and W. Q. Tao, “Study on the consistency between field synergy principle and entransy dissipation extremum principle”, Int. J. Heat Mass Transfer, Vol. 116, 2018, pp. 621-634.
[https://doi.org/10.1016/j.ijheatmasstransfer.2017.09.044]

-
L. Zhang, H. Y. Wei, and X. S. Zhang, “Theoretical analysis of heat and mass transfer characteristics of a counter-flow packing tower and liquid desiccant dehumidification systems based on entransy theory”, Energy, Vol. 141, 2017, pp. 661-672.
[https://doi.org/10.1016/j.energy.2017.09.118]

-
M. Xu, “The thermodynamic basis of entransy and entransy dissipation”, Energy, Vol. 36, No. 7, 2011, pp. 4272-4277.
[https://doi.org/10.1016/j.energy.2011.04.016]

-
X. T. Cheng and X. G. Liang, “Analyses of entropy generation and heat entransy loss in heat transfer and heat-work conversion”, Int. J. Heat Mass Transfer, Vol. 64, 2013, pp. 903–909.
[https://doi.org/10.1016/j.ijheatmasstransfer.2013.05.025]

-
K. H. Kim and K. Kim, “Comparative analyses of energy–exergy–entransy for the optimization of heat-work conversion in power generation systems”, Int. J. Heat Mass Transfer, Vol. 84, 2015, pp. 80‒90.
[https://doi.org/10.1016/j.ijheatmasstransfer.2015.01.002]

-
C. H. Han and K. H. Kim, “Entransy and exergy analyses for optimizations of heat-work conversion with carnot cycle”, J. Ther. Sci., Vol. 25, 2016, pp. 242-249.
[https://doi.org/10.1007/s11630-016-0856-9]

-
S. Wang, W. Zhang, Y. Q. Feng, X. Wang, Q. Wang, Y. Z. Liu, Y. Wang, and L. Yao, “Entropy, entransy and exergy analysis of a dual-loop organic rankine cycle (DORC) using mixture working fluids for engine waste heat recovery”, Energies, Vol. 13, No. 6, 2020, pp, 1301.
[https://doi.org/10.3390/en13061301]

-
T. Yang, G. J. Chen, and T. M. Guo, “Extension of the Wong-Sandler mixing rule to the three-parameter Patel-Teja equation of state: Application up to the near-critical region”, Chem. Eng. J., Vol. 67, No. 1, 1997, pp. 27-36.
[https://doi.org/10.1016/S1385-8947(97)00012-0]

-
J. Gao, L. D. Li, Z. Y. Zhu, and S. G. Ru, “Vapor–liquid equilibria calculation for asymmetric systems using Patel–Teja equation of state with a new mixing rule”, Fluid Phase Equilibria, Vol. 224, No. 2, 2004, pp. 213-219.
[https://doi.org/10.1016/j.fluid.2004.05.007]