상업용 리튬 배터리의 수명 예측을 위한 고속대량충방전 데이터 정규화 선형회귀모델의 적용

3.1 데이터의 파악

Severson 등³⁾은, 상업용 LFP/graphite (A123-APR18650M1A) 배터리를 사용하여, 제조업체가 권장하는 고속충전 속도인 3.6 C에서 6 C까지 충전 조건을 의도적으로 변경하여 72개의 다른 급속충전 조건을 사용하여 다양한 양상을 보이는 124개 셀의 데이터를 생성했다. LFP/graphite (A123-APR18650M1A) 배터리의 공칭 용량은 1.1 Ah, 공칭 전압은 3.3 V이다. 72개의 충전 정책(policy)은 ‘C₁ (Q₁ %)-C₂’로 나타낼 수 있는데, C₁-rate로 Q₁ % 충전상태(state of charge, SOC)까지, C₂-rate로 80% 충전상태까지 정전류(constant current, CC)로 충전한다. 다음은 동일하게 1 C-rate로 CC 충전하며 3.6 V cut-off voltage 도달 시 1/50 C cut-off current까지 정전압(constant voltage, CV)으로 진행한다. 다음 방전은 동일하게 4 C-rate로 CC 한 후 2.0 V cut-off voltage 도달 시 CV로 1/50 C cut-off current 도달까지 진행된다. 공칭 용량의 80% 즉, 0.88 Ah가 될 때까지 충방전하여, 최소 150, 최고 2,300 싸이클 수명을 갖는 셀들의 데이터를 생성하였다.

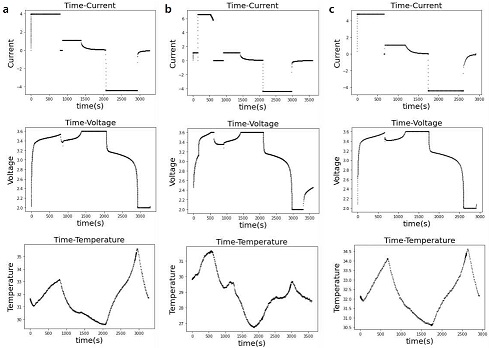
제공된 총 124개 셀의 CSV 파일 데이터 실험 날짜는 ‘2017-05-12’, ‘2017-06-30’, ‘2018-04-12’로 3개의 batch로 각 41, 43, 40개의 셀이다. Fig. 1은 데이터의 일부 예로, 기본적으로 전류, 전압, 온도 정보가 시간의 함수로 주어진다. 온도 증가는 충방전 시 전류가 인가될 때 일어나며⁴⁾ 열방출이나 흐름에 따라 최고온도는 전류가 감소된 후에 일어나는 것을 알 수 있다. ‘2017-05-12. 3.6 C (80%)-3.6 C’는 80% 충전 상태 도달 후 1분 휴식, 방전 후 1초 휴식, ‘2017-06-30. 1 C (4%)-6 C’는 80% 충전 상태 도달 후, 방전 후 모두 5분 휴식, ‘2018-04-12. 4.36 C (80%)-4.36 C’는 80% 충전 상태 도달 후, 내부 저항(internal resistance, IR) 측정 후, 1 C 충전 후, 방전 후 각 5초 휴식을 한 것을 알 수 있다. IR은 펄스법으로 별도로 싸이클 당 일회 측정하는데, 측정된 IR 값을 다음 싸이클에서 다시 측정할 때까지 시간에 따라 동일하게 기록하였다.

Fig. 1.

Example of data available at https://data.matr.io/1. Current, voltage and temperature as a function of time. (a) 2017-05-12, 3.6 C (80%)-3.6 C, (b) 2017-06-30, 1 C (4%)-6 C, (c) 2018-04-12, 4.36 C(80%)-4.36 C

3.2 용량 열화(capacity fade) 특성

Fig. 2 는 Severson 등³⁾의 논문에서 보고한 124개 셀의 용량 저하 양상의 기본 분석 결과를 그대로 재현한 것이다. 용량 열화곡선(capacity fade curve)을 나타내기 위해 로그 값을 적용한 각 배터리의 수명에 대해서 MinMaxScale을 적용 후 파이썬 matplotlib 패키지의 cm.coolwarmcolor를 적용하였다(Fig. 2[a]). MinMaxScale 식은 다음과 같다.

Fig. 2.

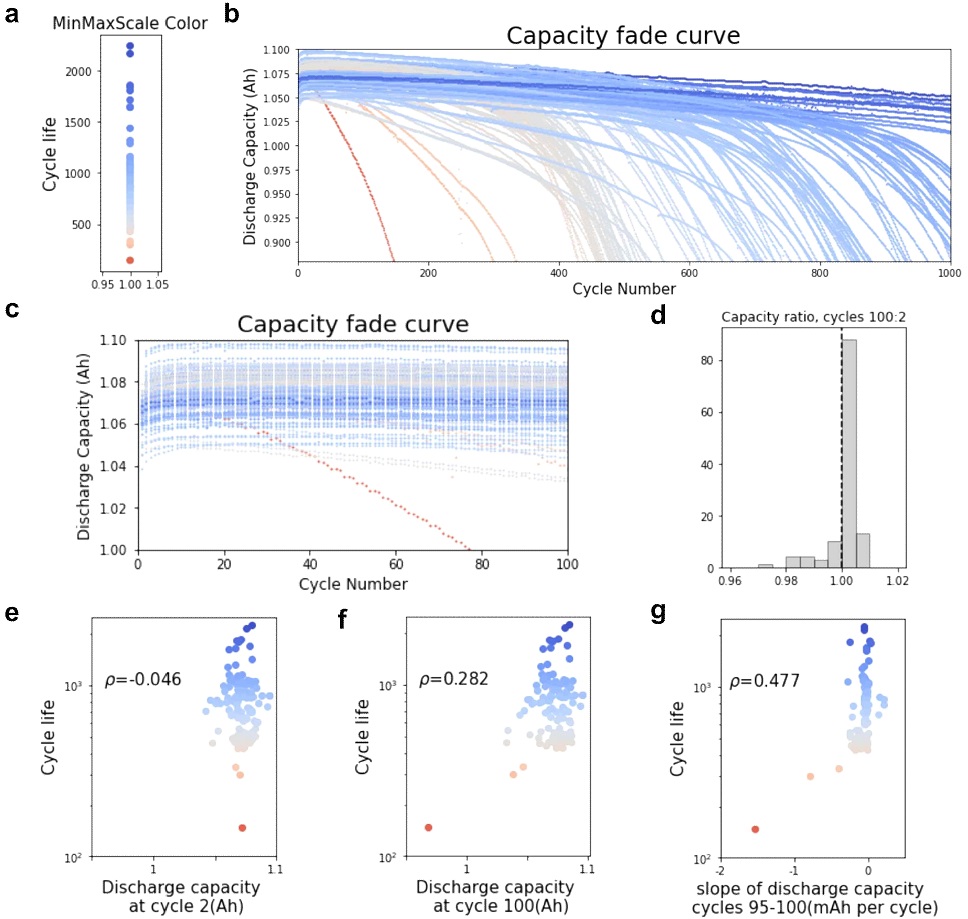
Reproduced Fig. 1 in Ref. [3]. (a) MinMaxScaled color of battery cycle life. (b) Reproduced 124 capacity fade curves (c) Capacity fade curve showing (a) up to 100 cycles (d). Cycle 100:2 capacity ratio (e). Cycle life as a function of discharge capacity at cycle 2. (f) Cycle life as a function of discharge capacity at cycle 100. (g) Cycle life as a function of the slope of the discharge capacity curve for cycles 95-100

Fig. 2(b), (c)는 각각 1,000 및 100 싸이클까지의 방전 용량 열화곡선을 나타낸 것이다. 100 싸이클까지 용량 열화가 거의 일어나지 않고 오히려 다소 증가하는데, Fig. 2(d)의 히스토그램에 100:2 싸이클의 용량 비율(capacity ratio) 값이 대부분 1 이상을 갖는 것을 나타내었다. 이 현상은 양극(cathode electrode)면적보다 음극(anode electrode)면적이 넓을 때 발생하는 돌출(overhang)영역 때문에 나타난다⁵⁾. 이 현상에 의해서 초기 싸이클에서 용량 열화가 적게 일어나게 되므로, Fig. 2(e)-(g)에서 나타내었듯이 2번째 싸이클의 용량, 100번째 싸이클의 용량, 또는 95와 100번째 싸이클의 변화량과 배터리의 수명과는, 각 p=-0.049, -0.276, -0.465 로 매우 낮은 피어슨 상관계수(pearson correlation coefficient, PCC)를 보인다. 다소 높아진 상관계수도, 수명이 매우 짧은, 이상치(outlier)에 해당하는 몇 개의 셀 데이터에 인한다. 즉, 100 싸이클 정도까지의 방전 용량과 배터리 수명이 약한 선형관계가 있음을 나타내며, 200 싸이클, 300 싸이클의 용량을 사용하여도 수명을 예측할 수 있는 선형관계를 보기 어렵다. 이는 초기 또는 상당한 충방전 후의 용량 열화 양상으로부터, 배터리 수명 예측이 잘 되지 않는다는 것을 보여준다.

3.3 용량 열화(capacity fade) 데이터의 머신러닝 접근

Severson 등³⁾의 논문에 기술된 대로, ‘2017-05-12’, ‘2017-06-30’, ‘2018-04-12’ 데이터를 batch 1, batch 2, batch 3으로 설정하고 batch 1, batch 2를 합쳐서 짝수 번째를 train 데이터, 홀수 번째를 primary test 데이터(마지막 데이터는 짝수 번째이지만 primary test 데이터로 설정), batch 3를 secondary test 데이터로 만든다. train 데이터가 41개로 예측 모델에 학습시키고, primary test 데이터가 43개로 train 데이터로 학습시킨 예측 모델을 검증하고, secondary test 데이터가 40 개로 검증 후에 테스트를 하게 된다. secondary test 데이터인 batch 3 셀 들은, batch 1과 2 셀들과 같이 준비되었으나, 측정 시작 날짜가 batch 1과 11개월 후이므로 캘린더노화 효과를 고려해야 할 수 있다. 참고문헌과 같이, Fig. 3을 비롯한 본 연구의 모든 그래프에서 train 데이터는 파랑, primary test 데이터는 빨강, secondary test 데이터는 주황색으로 나타내었다.

Fig. 3.

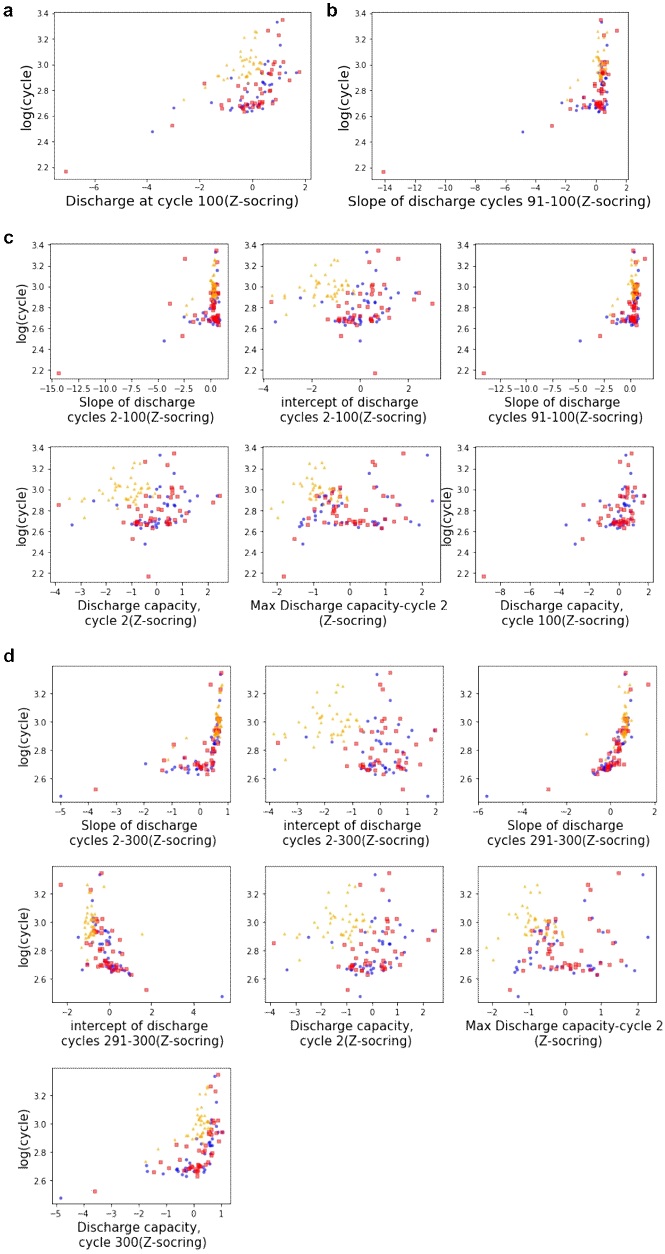
Features used in different models. (a) ‘discharge at cycle 100’, (b) ‘slope of discharge cycles 91-100’, (c) ‘multivariate discharge curve model, cycle 100’, (d) ‘multivariate discharge curve model, cycle 300’. Blue, red, and orange colors represent each train, primary test, and secondary test. The Z-scored feature values are presented on the X-axis. Z-scoring is performed based on the training data

벤치마킹 모델인 3개의 용량 열화곡선 일변량 모델(univariate model)과 2개의 용량 열화곡선 다변량 모델(multivariate model)로 회귀(regression) 분석을 재현했다. 첫 번째 모델은 ‘constant’로 수명의 평균만을 사용하여 회귀를 진행하였는데, ‘constant’는 수명 값을 이미 알고 있게 되는 데이터가 되므로 학습의 의미가 없어 두 번째 모델부터 학습을 진행했다.

Fig. 3에 나머지 모델의 데이터를 플롯하였는데, 모든 feature에 대해 표준화 (standardization, Z-scoring)이 필요한데, train 데이터의 평균과 표준편차를 사용하여 표준화하였다. Fig. 3(a)에 나타낸 ‘discharge at cycle 100 (100번째 싸이클의 방전용량)’으로 오직 100 싸이클에서 방전 용량만 feature 로 사용하여 회귀를 진행, Fig. 3(b)는 ‘slope of discharge cycles 91-100’으로 용량 열화곡선의 91-100 싸이클에서 선형 피팅(fitting) 후 기울기만 feature로 사용하여 회귀 진행, Fig. 3c 는 ‘Multivariate discharge curve model, cycle 100’으로 1) slope of discharge cycles 2-100 (싸이클 2와 100 사이 선형 피팅의 기울기), 2) intercept of discharge cycles 2-100 (절편), 3) slope of discharge cycles 91i100 (91-100 사이의 기울기), 4) discharge capacity, cycle 2 (2번째 싸이클의 방전 용량), 5) Max discharge capacity - discharge capacity, cycle 2 (최고 용량과 2번째 싸이클 용량과의 차이), 6) discharge capacity, cycle 100 (100번째 싸이클의 용량), 6개의 feature로 회귀를 진행. Fig. 3(d)는 ‘Multivariate discharge curve model, cycle 300’으로 1) slope of discharge cycles 2-300 (싸이클 2와 300 사이 선형 피팅의 기울기), 2) intercept of discharge cycles 2-300 (절편), 3) slope of discharge cycles 291-300 (291-300 사이의 기울기), 4) intercept of discharge cycles 291-300 (절편), 5) discharge capacity, cycle 2 (2번째 싸이클의 방전 용량), 6) max discharge capacity - discharge capacity, cycle 2 (최고 용량과 2번째 싸이클 용량과의 차이), 7) discharge capacity, cycle 300 (300번째 싸이클의 용량), 7개의 features로 회귀를 진행하였는데, 300 싸이클 이하 150싸이클 수명의 ‘b2c1’ 데이터는 제외하였다.

모든 feature에 대해서 특성별 표준화를 진행 후 정규화(regularization)된 선형회귀 모델 3가지 Lasso, Ridge, Elastic Net의 최적의 hyperparameter를 찾는데 4-겹 교차 검증(4-fold cross validation)을 적용해서 학습했다. 선형회귀는 mean square error (MSE) 값을 최소화하는 것으로 MSE는 다음과 같으며 모델의 예측 값과 실제 값의 차이를 제곱 평균한 것이다.

MSE는 비용함수(cost function), 손실함수(loss function)라고 부르며 이 값이 최소가 되도록 하는 것을 최소제곱법(ordinary least squares, OLS)이라 부른다. 이렇게 얻은 모델이 훈련데이터에 잘 맞지만 일반성이 떨어질 때 과대적합(overfitting) 되었다고 표현한다. 과대 적합은 훈련데이터의 노이즈가 크고 모델이 너무 복잡할 때 일어난다. 과대적합을 해결하기 위해서 모델에 규제(penalty)를 가해서 가중치를 제한한다. 선형회귀 모델인 Lasso, Ridge, Elastic Net은 손실함수에 규제가 추가되어 다음과 같이 주어진다^6,7).

회귀모델의 평가로 root mean square error (RMSE), mean percentage error (MPE)를 사용한다.

Fig. 4는 ‘Discharge at cycle 100’ 모델의 정규화된 Ridge, Lasso, Elastic Net 선형회귀 예측 결과이다. 데이터의 경향이 실선을 따라 움직일 때 잘 학습되고 잘 예측하는 모델이 되는데 ‘Discharge at cycle 100’ 모델의 결과는 실선 아래로 분포하는 모습을 볼 수 있다. Table 1에 나타낸 Train, Primary test, Secondary test의 MPE가 대략 21.8%, 23.0%, 39.5%로 모델이 과소적합(underfitting) 되어있는 것을 볼 수 있으며 큰 RMSE 값을 볼 수 있다. 앞에서 나타낸 MPE는 Ridge, Lasso, Elastic Net에서 최솟값을 나타낸 것으로 최솟값이 나타나는 모델이 적절함을 나타낸다. Secondary test 예측에서는 더 큰 오차(error)가 발생함을 볼 수 있는데, 큰 오차는 데이터의 수가 작거나, 노이즈가 섞여 있거나, 간단한 선형회귀 모델에 복잡한 feature을 학습시킬 때 발생할 수 있는데, secondary test 데이터는 train, primary test 데이터와 비교 측정 시작 10-11개월 지난 시점에서 측정된 것이므로, 캘린더 노화에 따른 효과로 추론할 수도 있는데, 이를 고려하는 데이터 feature 이 머신러닝에 필요할 것이다.

Fig. 4.

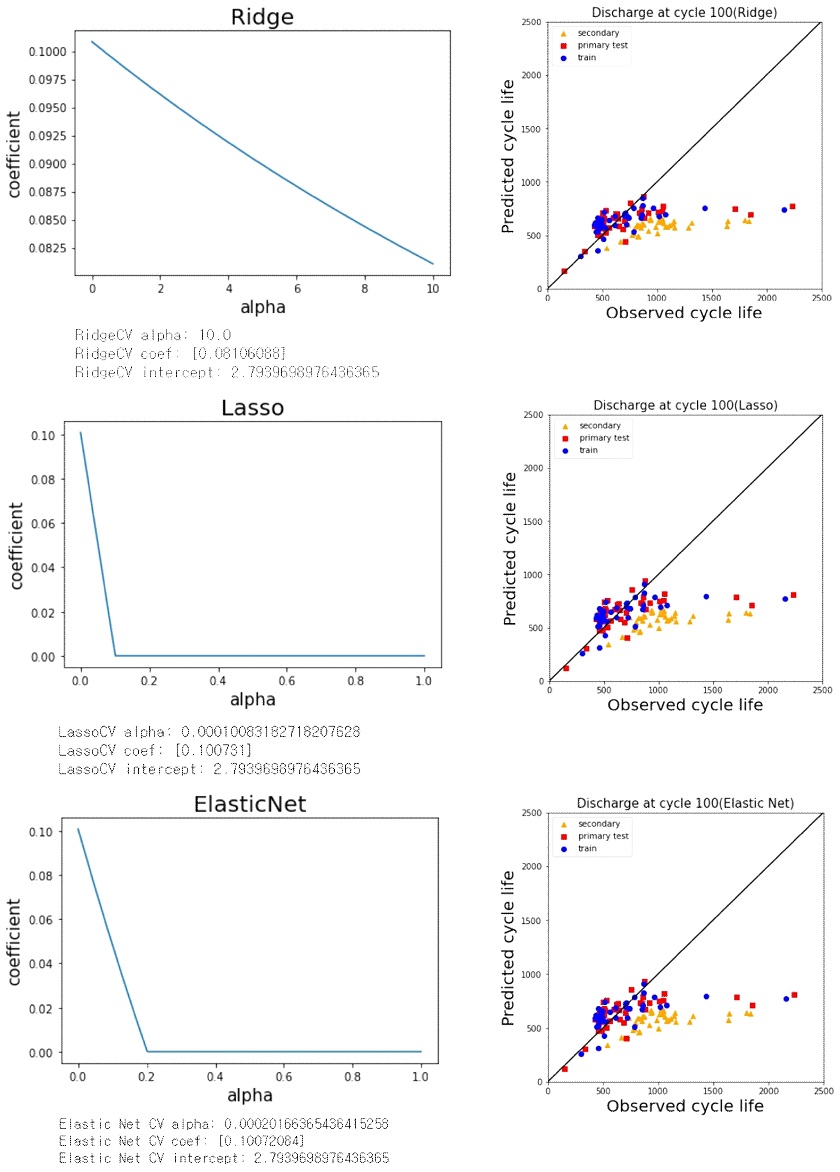
Linear regression prediction result with Ridge, Lasso, and Elastic Net regularization of ‘Discharge at cycle 100’ model of Fig. 3(a)

Table 1.

RMSE, MPE result of ‘Discharge at cycle 100’ model

Fig. 5는 ‘Slope of discharge cycles 91-100’ 모델의 정규화된 Ridge, Lasso, Elastic Net 선형회귀 예측 결과이다. Fig. 4의 ‘Discharge at cycle 100’ 모델 결과보다 더 실선에서 벗어나 평탄한 양상을 볼 수 있다. Table 2에 나타낸 MPE는 train, primary test, secondary test가 대략 24.7%, 25.6%, 33.4%로 과소 적합이 더 심하게 된 것을 볼 수 있으며 앞 모델과 마찬가지로 RMSE가 크고 secondary test 예측에서 더 큰 오차가 발생함을 볼 수 있다.

Fig. 5.

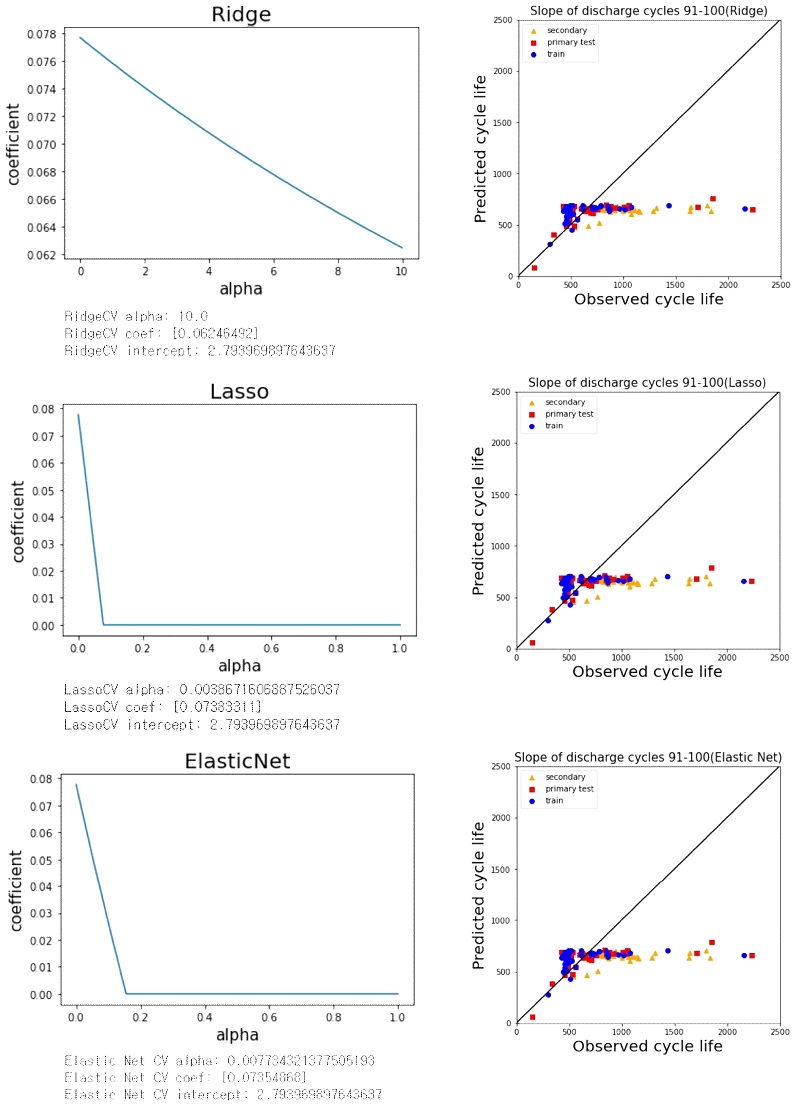
Linear regression prediction result with Ridge, Lasso, and Elastic Net regularization of ‘Slope of discharge cycles 91-100’ model of Fig. 3(b)

Table 2.

RMSE, MPE result of ‘Slope of discharge cycles 91~100’ model

Fig. 6은 feature을 6개 사용한 ‘Multivariate discharge curve model, cycle 100’ 모델의 결과이다. Severson 등³⁾의 논문의 그래프와 유사하도록 그래프 사이즈를 조정하였다. 용량열화곡선의 feature을 6개로 늘렸음에도 불구하고 train, primary test, secondary test의 MPE가 대략 24.2%, 25.3%, 37.0%로 과소적합이 심한 것을 볼 수 있다(Table 3). 마찬가지로 RMSE가 크고 secondary test 예측에서 더 큰 오차가 발생함을 볼 수 있다. Lasso나 Elastic Net의 상관계수 값이 0이 되는 feature을 볼 수 있는데 이는 결과를 얻는데 불필요한 feature가 0이 된 것이다. Lasso에서는 ‘slope of discharge cycles 2-100’, ‘max discharge capacity-discharge capacity, cycle 2’이 불필요한 feature이고, Elastic Net에서는 ‘slope of discharge cycles 2-100’, ‘intercept of discharge cycles 2-100’, ‘max discharge capacity-discharge capacity, cycle 2’ 이 불필요한 feature임을 볼 수 있다.

Fig. 6.

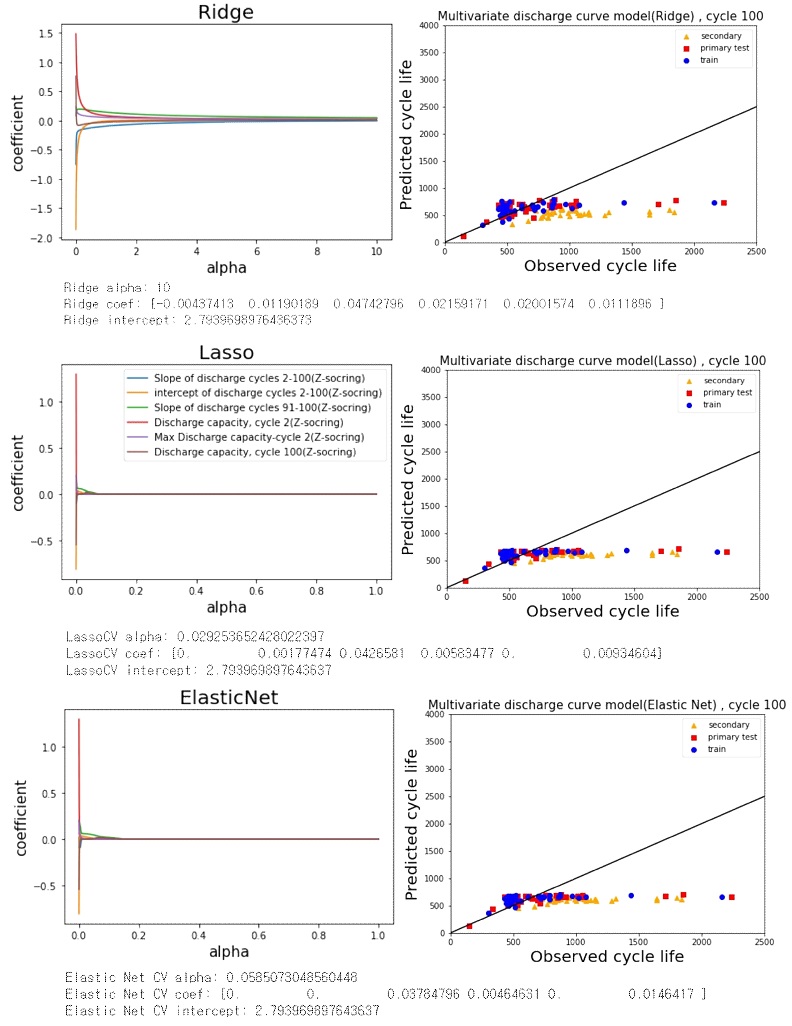
Reproduced Supplementary Fig. 8 in Ref. [3]. Linear regression prediction result with Ridge, Lasso, and Elastic Net regularization of ‘Multivariate discharge curve model, cycle 100’ model of Fig. 3(c)

Table 3.

RMSE, MPE result of ‘Multivariate discharge curve model, cycle 100’

Fig. 7은 feature을 7개 사용한 ‘Multivariate discharge curve model, cycle 300’ 모델의 결과이다. 마찬가지로 참고문헌과 비슷하게 그래프를 조정하였다. Feature을 7개로 늘렸음에도 불구하고 train, primary test, secondary test의 MPE가 대략 19.6%, 22.3%, 32.3%로 과소적합이 심한 것을 볼 수 있다(Table 4). 마찬가지로 RMSE가 크고 secondary test 예측에서 더 큰 오차가 발생함을 볼 수 있다. ‘slope of discharge cycles 2-300’, ‘intercept of discharge cycles 2-300’, ‘intercept of discharge cycles 291-300’, ‘discharge capacity, cycle 2’, ‘max discharge capacity-discharge capacity cycle 2’가 불필요한 feature임을 볼 수 있다.

Fig. 7.

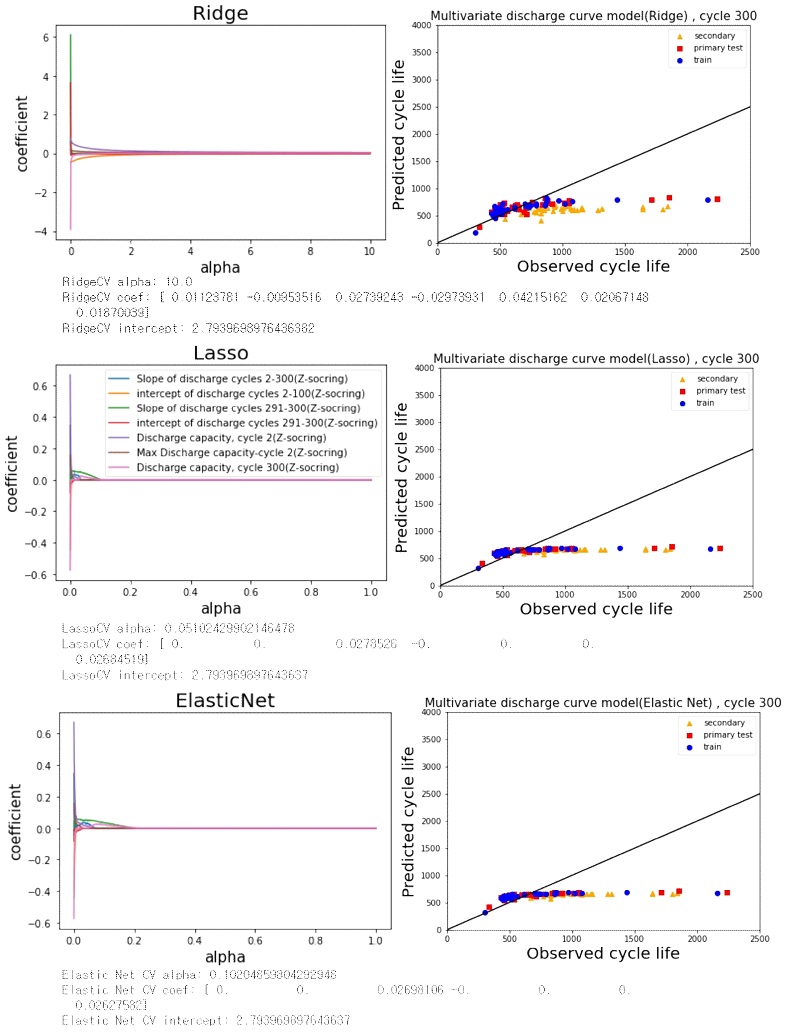
Reproduced Supplementary Fig. 9 in Ref. [3]. Linear regression prediction result with Ridge, Lasso, and Elastic Net regularization of ‘Multivariate discharge curve model, cycle 300’ mode of Fig. 3(d)

Table 4.

RMSE, MPE result of ‘Multivariate discharge curve model, cycle 300’

3.4 방전전압곡선 feature의 머신러닝 활용

상기의 결과는 방전 용량 열화곡선에서 얻은 특성을 사용한 머신러닝 접근으로는, 수백 싸이클까지의 초기 충방전 용량 결과를 사용하고도, 배터리의 수명 예측을 제대로 할 수 없다는 것을 보였다. Severson 등³⁾의 연구 결과의 하이라이트는 다음에 기술하듯이 전압곡선 feature을 활용할 경우 초기 100 싸이클까지 정도의 데이터를 사용해서도, 배터리의 수명 예측을 9.1 % 오차내에서 가능함을 보였다는 것이다.

Fig. 8에 나타낸 방전전압곡선에서 capacity fade feature은 2.0 V cut-off에서의 n번째 싸이클의 용량 값 Q_n데이터를 사용한 것인데, 모든 싸이클 데이터가 cut-off 전압 조건에 의해서 전압값이 2.0 V-3.5 V 사이로 동일하게 제한되므로 동일한 전압 값에 대해, 싸이클에 따라, 용량의 변화 양상을 사용하는 것이다. 다른 싸이클의 동일한 전압에서의 용량 값을 비교하기 위해서는 데이터 처리가 필요한데, Fig. 1에 나타냈듯이 정해진 C-rate (4 C)로 일정한 전류를 가하고, 일정한 시간간격으로 측정한 데이터는 일정한 간격의 용량에 해당하여 전압값은 일정하지 않다. Fig. 8(a) 의 실제 측정 데이터가 충분히 촘촘하게 측정되었으므로, 모든 방전 데이터를 2.0 V-3.5 V에서 선형으로 간격을 둔 1,000개의 전압 지점에서 스플라인 선형 보간 피팅(spline linear interpolation fitting)을 하면, Fig. 8(b)에 나타낸 것과 같이, 실제 데이터의 곡선과 거의 일치하게 되고 같은 전압 지점에서 방전 용량 값을 얻거나 싸이클 간의 차이 등을 구할 수 있다. Lee와 Lim¹⁾의 연구 데이터 링크에 이와 같이 작업된 데이터들도 제공되어 있다. 본 연구에서는 데이터 처리를 확인해 보고, 제공된 피팅 데이터를 사용하였다.

Fig. 8.

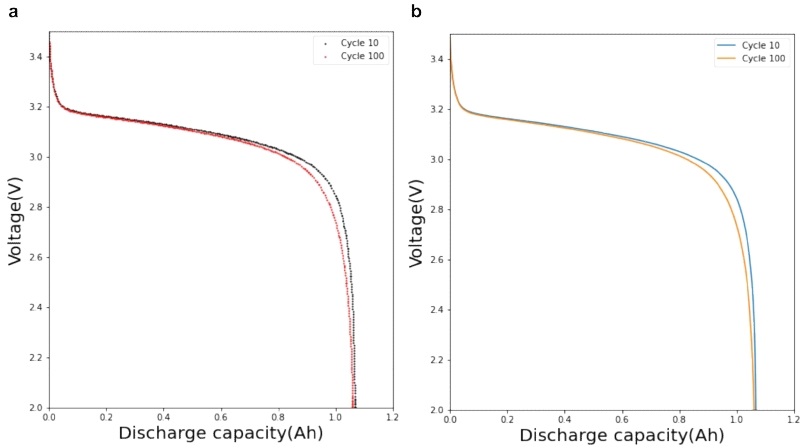
Reproduced Fig. 2(a) in Ref. [3]. Sample ‘b1c30’ discharge voltage curve for 100th and 10th cycles. (a) Raw data curve. (b) Spline linear interpolation fitted curve

전압 값에 따라 정리된 방전곡선 데이터를 사용하여 Fig. 9(a) 에 전체 124개 셀의 100번째 싸이클과 10번째 싸이클의 차이와 전압의 관계 ΔQ_100-10(V)를 나타낼 수 있는데, Fig. 2와 같이 각 셀의 수명에 따른 칼라로 나타내었다. 본 연구에서 만든 그래프는, 재현된 논문의 그래프, Fig. 9(b)와 차이가 있는데, 제외가 명시된 짧은 수명의 셀 데이터(빨간색) 외에도, 오른쪽으로 돌출된 부분이 있는, 즉, 100번째 싸이클의 용량이 10번째보다 큰 부분이 있는 셀 들은 나타내지 않았음을 알 수 있었다(‘b2c1’, ‘b3c16’, ‘b3c17’, ‘b3c42’, ‘b3c43’ 데이터를 나타내지 않았음을 확인할 수 있었다). 예외적인 데이터, 이상치들이 머신러닝에서 학습에 방해가 되므로 적절히 제거해야 하나 유의미한 양상들이 배제될 수 있으므로 주의해야 한다. 직접적으로 확인할 수는 없으나 본 연구에서 재현한 머신러닝 결과와 Severson 등³⁾의 논문의 결과가 차이가 있는 것은 고려한 데이터세트가 정확히 일치하지 않는 요인도 있다고 추정된다.

Fig. 9.

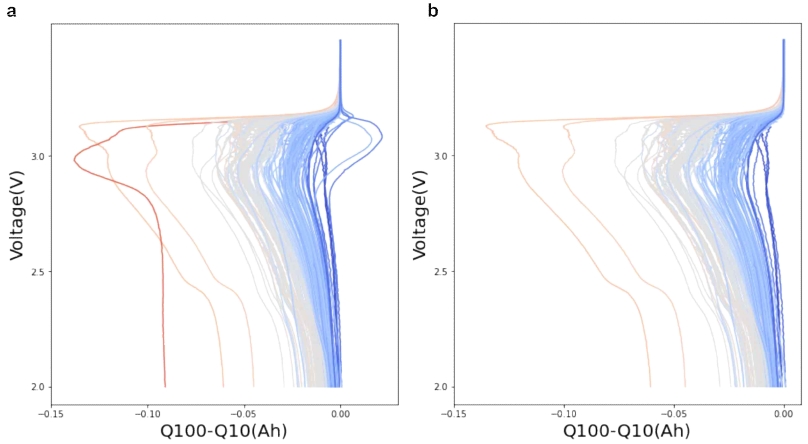
Reproduced Fig. 2(b) in Ref. [3]. Difference of the discharge capacity curves as a function of voltage between the 100th and 10th cycles, ∆Q100-10(V), for 124 cells. (a) Full data. (b) Outlier removal data

Fig. 9의 곡선들이 수명을 나타내는 색깔의 순서로 정렬된 양상을 보여주는 것을 알 수 있다. 즉 파랑색의 수명이 긴 셀들은 ΔQ_100-10(V) 이 0에 가깝게 작고 전압에 대한 변화가 작은 반면 수명이 짧은 셀들은 전압에 따라 큰 변화를 보이고 차이가 크다. 이러한 초기 싸이클 특성을 사용하여 배터리의 수명예측이 잘 될 수 있으리라는 것을 보여준다. Fig. 9의 양상을 잘 나타내는 feature 로, 평균값, 최솟값, 최댓값 등 보다 분산(variance) 값임을 알 수 있다. Fig. 10(a) (left)에 로그 분산 값, Var(ΔQ_100-10[V])과 로그 수명 값이 피어슨 상관계수 p=-0.92를 보임을 나타내었다.

Fig. 10.

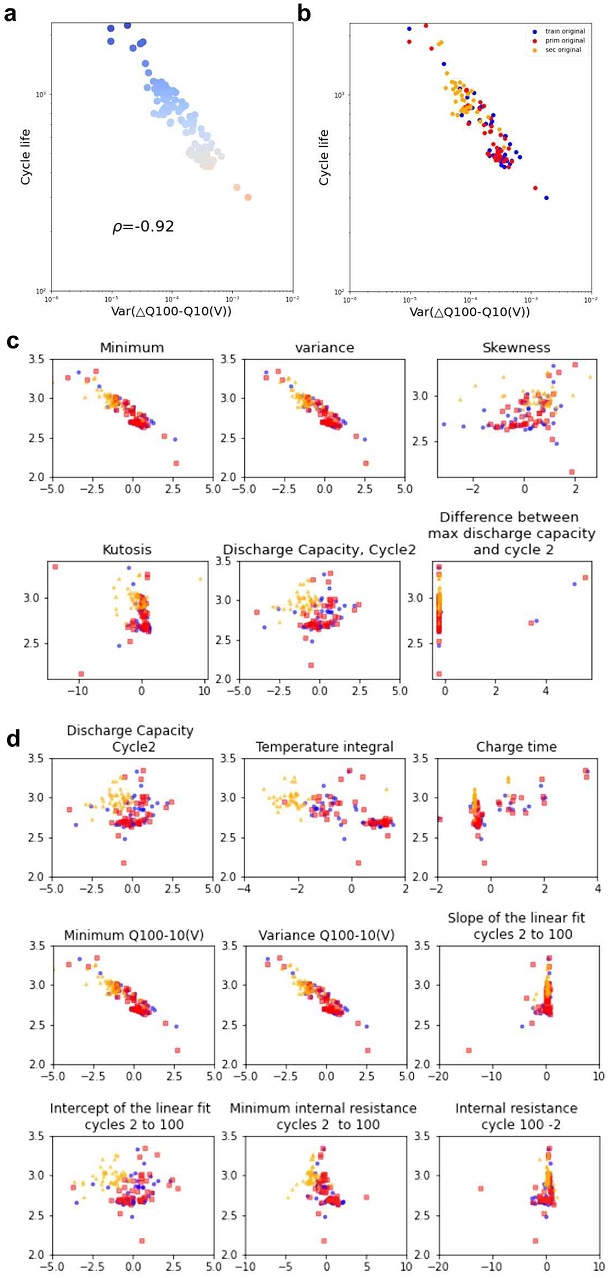
(a) Difference of the discharge voltage curves as a function of voltage between the 100th and 10th cycles, ΔQ100-10(V), for 124 cells. (Reproduced Fig. 2[c] in Ref. [3]); (b) ‘variance' model data, supplementary Fig. 5 in Ref. [3]. (c) 6 features of 'Discharge' model (d) 9 features of 'Full' model data

3.5 방전전압곡선 feature의 머신러닝 접근법

Severson 등³⁾의 방전전압 곡선(discharge voltage curve)으로부터 추출한 feature 를 사용한 ‘Variance’, ‘Discharge’, ‘Full’ 모델을 재현했다. ‘Variance’ 모델은 Fig. 10(a)의 분산을 feature로 사용하여, 앞 단원과 마찬가지의 train, primary test, secondary test로 나눈 데이터로 회귀를 진행한다(Fig. 10[a], [b]). Fig. 10(b)에서 주목할 점은 주황색으로 나타낸 secondary test 데이터가 캘린더 노화가 있었을 것으로 생각됨에도 불구하고 로그-로그 그래프에서 batch 1과 2의 train 데이터와 primary test 데이터가 일관된 양상을 보인다는 것이다. Variance 로 나타나는 셀 수명특성보다 캘린더 노화 특성의 효과가 두드러지지 않는다고 볼 수도 있다.

Fig. 10(c)에 나타낸 ‘Discharge’ 모델은 ΔQ_100-10(V) 그래프(Fig. 9[b])의 1) minimum (최솟값), 2) variance (분산), 3) skewness (비대칭도), 4) kurtosis (첨도)와, (앞 절에서 다룬) 용량 열화곡선에서(Fig. 2) 5) discharge capacity, cycle 2 (2번째 싸이클의 방전용량), 6) difference between max discharge capacity and cycle 2 (최대 방전 용량 값과 두 번째 싸이클 용량의 차이), 6개의 feature을 사용하여, 회귀를 진행하였다. Fig. 10(d) 에 나타낸 ‘Full’ 모델은 i) ΔQ_100-10(V)의 1) minimum (최솟값), 2) variance (분산)과 ii) 용량열화곡선으로부터 3) slope of the linear fit to the capacity fade curve, cycles 2 to 100 (싸이클 2와 100 사이 선형 피팅의 기울기), 4) intercept of the linear fit to capacity fade curve, cycles 2 to 100 (절편), 5) discharge capacity, cycle 2 (2번째 싸이클의 방전용량), iii) 기타 데이터로부터 feature 로 6) average charge time, first 5 cycles (초기 5 싸이클의 평균 충전 시간), 7) Integral of temperature over time, cycles 2 to 100 (싸이클 2와 100 사이 온도의 적분 값), 8) minimum internal resistance, cycles 2 to 100 (싸이클 2와 100 사이에서 IR 최솟값), 9) internal resistance, difference between cycle 100 and cycle 2 (싸이클 2와 100의 IR값의 차이), 총 9개의 feature를 사용하는 ‘Full’ 모델을 재현했다. 기타 다른 feature 은 Fig. 1과 3.1절에 기술한 raw 데이터에서 제공되는 데이터이다. 앞의 3.3절에서 용량열화 데이터로부터 추출한 feature를 이용한 모델 분석과 마찬가지로, 모든 feature에 대해서 표준화를 진행하여 데이터를 만든 후 정규화된 선형회귀 모델 3가지 Lasso, Ridge, Elastic Net으로 4-겹 교차 검증을 적용해서 학습했다. 회귀모델의 평가로 RMSE, MPE를 사용한다.

3.6 전압곡선의 feature를 사용한 배터리 수명 예측

Fig. 11은 ΔQ_100-10(V)의 분산 특성만 사용한 ‘Variance’ 모델의 정규화된 Ridge, Lasso, Elastic Net 선형회귀 예측 결과이다. Table 5에 나타낸 것과 같이 train, primary test, secondary test의 MPE가 대략 14.1%, 14.8%, 11.1%가 나타났으며 RMSE 역시, 앞서 용량열화곡선의 feature 을 사용하여 예측한 것보다 좋은 결과를 볼 수 있다.

Fig. 11.

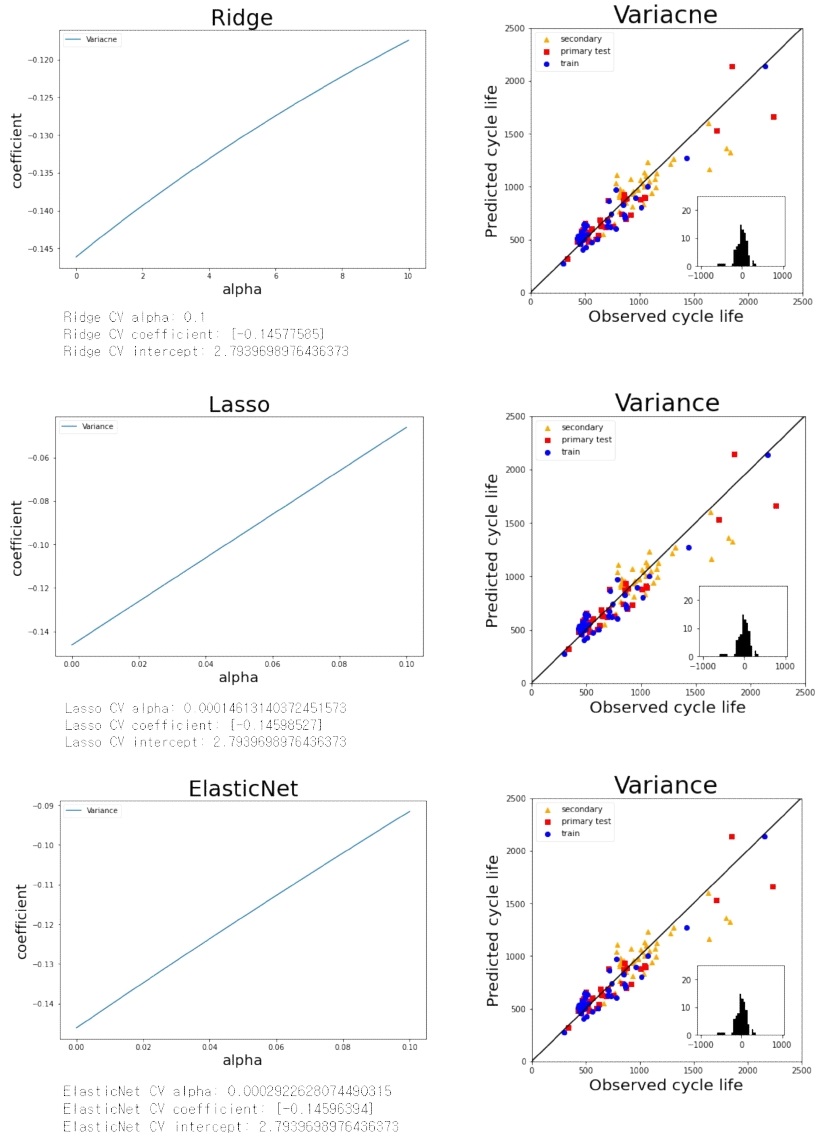
Reproduced Fig. 3(a) in Ref. [3]. Linear regression prediction result with Ridge, Lasso, and Elastic Net regularization of ‘Variance’ model. The inset shows the histogram of residuals (predicted-observed) for the primary and secondary test data

Table 5.

RMSE, MPE result of ‘Variance’ model

Fig. 12는 ΔQ_100-10(V) 데이터에서 4개, 용량 열화곡선 데이터에서 2개, 총 6개의 특성을 사용한 ‘Discharge’ 모델의 결과이다. Train, primary test, secondary test의 MPE가 대략 9.8%, 15.7%, 11.7%가 나타났다(Table 6). Ridge regression 과 달리, Lasso, Elastic Net에서 상관계수 값이 0이 되는 불필요한 특성을 알려주는데 수명과 분명한 상관관계를 보이는 ‘variance’가 0이 되는 의외의 결과가 나왔다(Minimum이 가장 높은 상관계수를 보였다).

Fig. 12.

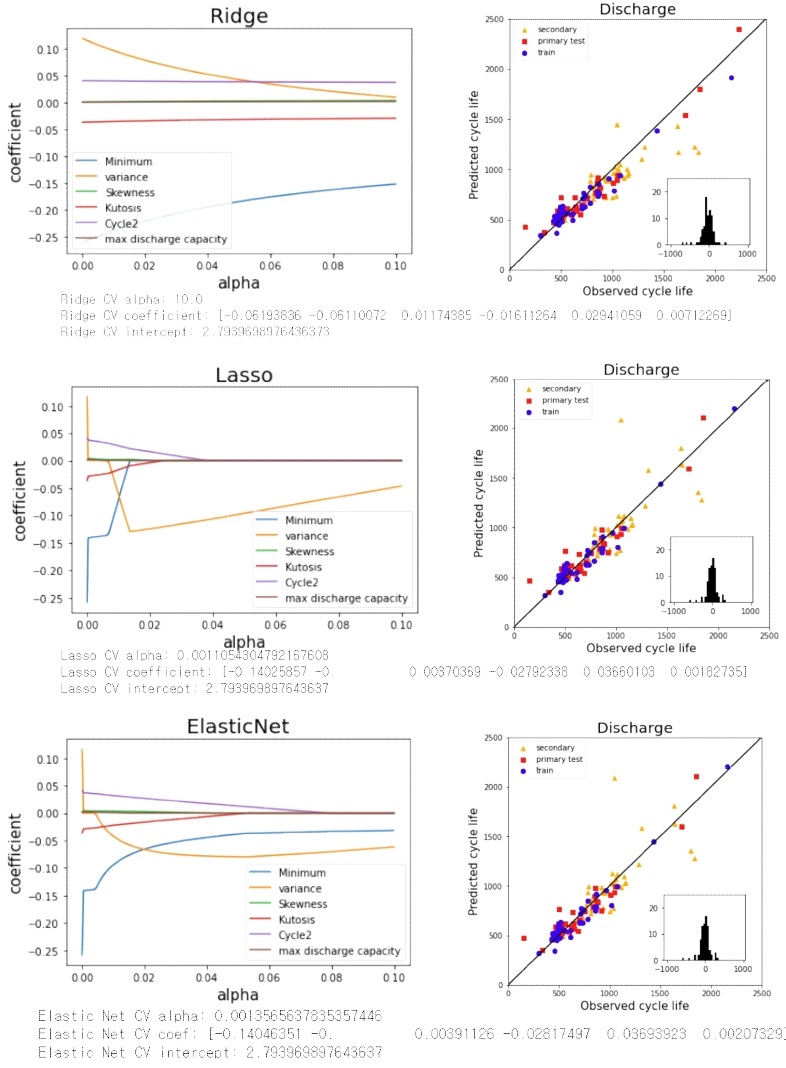
Reproduced Fig. 3(b) in Ref. [3]. Linear regression prediction result with Ridge, Lasso, and Elastic Net regularization of ‘Discharge’ model

Table 6.

RMSE, MPE result of ‘Discharge’ model

이는 alpha 값이 낮은 곳에서 variance 데이터와 비슷한 데이터 형태를 갖는 minimum 데이터가 가장 영향력이 강한 것을 볼 수 있으며, 제약을 어느정도 준 곳에서는 variance 가 영향력이 가장 강한 것을 볼 수 있다. minimum, variance 데이터의 구조가 비슷하기 때문에 4-겹 교차검증으로 얻어낸 최적의 하이퍼파라미터는 variance를 제거한 것으로 보여진다.

Fig. 13은 ΔQ_100-10(V)의 feature와 용량 열화곡선에서의 feature, 시간, 온도, IR 등과 같은 특성들의 조합으로 9개의 특성을 사용한 ‘Full’ 모델의 결과이다. Train, primary test, secondary test의 MPE가 대략 5.4%, 12.4%, 11.9%가 나타났으며(Table 7) Lasso, Elastic Net에서 상관계수 값이 0 이 되는 불필요한 feature 로 용량열화곡선에서 추출한 feature인 ‘slope of the linear fit to the capacity fade curve, cycles 2 to 100’, ‘intercept of the linear fit to capacity fade curve, cycles 2 to 100’이 나타났다. 이것은 앞서 이러한 용량열화곡선의 feature 들로 regression 한 결과가 수명예측이 잘 되지 않은 것과 일치한다.

Fig. 13.

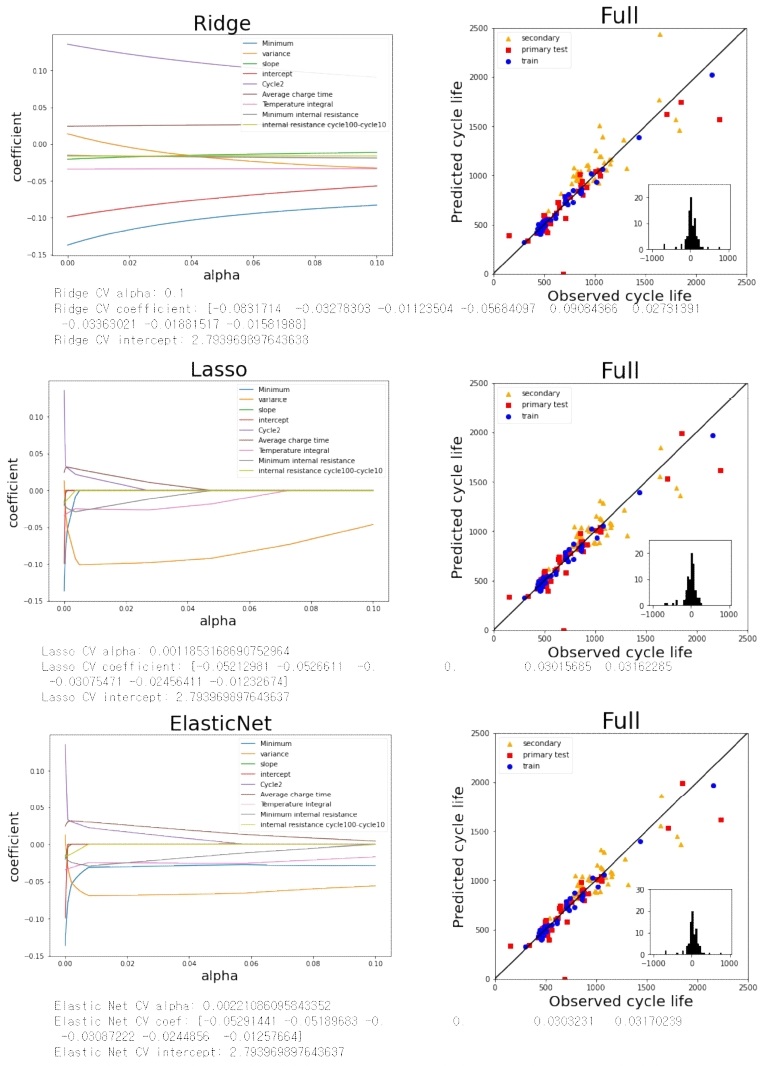
Reproduced Fig. 3(c) in Ref. [3]. Linear regression prediction result with Ridge, Lasso, and Elastic Net regularization of ‘Full’ model

Table 7.

RMSE, MPE result of ‘Full’ model

‘Variance’, ‘Discharge’, ‘Full’ 모델의 실제수명과 예측한 수명을 비교한 그래프를 보면 실선을 따라 움직이는 경향이 보이게 되며, 초기 싸이클 데이터는 ‘variance’ 특성만 사용함에도 좋은 결과를 얻어낼 수 있다. 용량열화곡선 특성만 사용한 결과보다 전압곡선 특성을 사용한 모델이 MPE가 더 낮게 나타났으며, 다양한 특성을 조합한 ‘Full’ 모델의 MPE가 가장 낮은 모습을 나타냈다. Figs. 11-13 및 Table 2의 결과는 Severson 등³⁾의 결과와 100% 일치하지 않는다. ‘Full’ 모델의 primary test 와 secondary test 의 평균 MPE 12.2% 는 Severson 등³⁾이 보고한 최적의 결과로 발표한 9.1% 보다 크다. 이는 제거된 이상치 데이터의 구체적인 전체 정보가 주어지지 않아, 정확히 같지 않을 수 있고, regression에서 사용된 하이퍼파라미터도 제시되지 않았는데, 일반적으로 같지 않기 때문이다. 동일한 데이터와 동일한 하이퍼파라미터를 사용하면 동일한 결과가 얻어진다.

3.7 물리적 의미의 고찰

Severson 등³⁾은 초기 싸이클 동안 용량 감소로는 나타나지 않으나, 방전전압곡선의 양상인ΔQ_100-10(V)곡선에서 드러나는 배터리의 수명 특성의 물리적 메카니즘도 추가 실험 데이터와 문헌⁵⁾으로 설명하였다. 초기 싸이클에 solid electrolyte interphase (SEI)가 성장함에 따라 리튬 도금과 같은 반응에 소모되며 양극, 음극 사이의 싸이클링에 사용할 수 없게 되는 loss of lithium inventory (LLI)가 일어나고 이는 용량 감소로 이어지게 된다. LLI는 온도, C-rate가 증가함에 따라 증가한다. 하지만 방전 저전압하에서, 양극보다 넓은 흑연 전극의 overhang 영역에서 리튬이 공급되면서 초기 용량 저하가 나타나지 않기 때문에 용량 열화곡선은 배터리의 수명과의 연관을 잘 보여주지 않는다. 하지만 이러한 반응은 리튬이 탈리된(delihiated) 상태의 음극 활물질이 줄어드는 것, loss of active material of the delithiated negative electrode (LAM_deNE)이 일어나므로 graphite 전위가 변경됨에 따른 전압곡선의 이동이 일어나고, 전압에 따른 용량 손실의 불균일, 즉, 큰 분산을 보이게 된다. LAM_deNE가 일어난 시점에서 충전하는 동안 리튬 이온을 수용하는 면적이 충분하지 않아서 리튬 도금을 유도하고 용량 저하가 가속화된다. 이런 관찰은 LAM_deNE가 초기 싸이클에서 용량 열화를 나타내지 않기 때문에 방전전압곡선을 기반으로 한 모델이 용량 열화곡선을 기반으로 한 특성만 사용하는 모델보다 오류가 더 낮은 이유가 된다. 방전전압곡선의 분산 feature만 사용한 'Variance' 모델은 용량 열화곡선 feature만 사용한 모델보다 좋은 결과가 나타난다. 그러나 한 가지 feature만 사용하는 것보다 물리적 의미를 알고 있는 다양한 feature를 조합하여 학습시키는 것이 더 좋은 결과를 얻어낼 수 있다. 가장 좋은 결과를 나타낸 ‘Full’ model의 feature는 용량 열화곡선, 방전전압곡선, 온도, IR에 추출한 다양한 feature를 사용하였는데, 추가적인 feature 테스트해볼 수 있다.