비선형 동특성 모델을 통한 전해막 습증기 함유도 특성 예측
2021 The Korean Hydrogen and New Energy Society. All rights reserved.
Abstract
Water management is essential to improve the performance of proton exchange membrane fuel cells. This study targets to understand the characteristics of water concentration in proton exchange membrane fuel cells at a dynamic load variable environment. The fuel cell model was developed to simulate nonlinear water transport in membrane by the MATLAB/Simulink® (MathWorks, Natick, MA, USA) platform, and it calculates water content in membrane, ionic conductivity, and predicts fuel cell performance through one-dimensional analysis.
Keywords:
Proton exchange membrane fuel cell, Water transport, Water content, Dynamic model키워드:
이온 교환막 연료전지, 수분 수송, 습증기 함유도, 통특성 모델1. 서 론
현재 화석연료를 바탕으로 하는 기존 시스템들은 연료 매장량의 고갈과 지구온난화 등의 환경 문제로 인해서 한계상황에 직면에 있다. 그 대안 중 하나로수소를 에너지원으로 하는 연료전지 또한 주목받고 있다1,2). 이온 교환막 연료전지(proton exchange membrane fuel cell, PEMFC)는 저온에서의 응답성이 좋고 고효율, 고전류 운전이 가능할 뿐만 아니라 부하변화에 대한 응답특성이 빨라 기존 내연기관을 대체할 수송용, 발전용 동력 발생원으로 개발되고 있다. 또한 이온 교환막 연료전지는 NOx, SOx 등 대기오염물질을 배출하지 않는 환경 친화적인 특성3)을 가지고 있어 차세대 차량 에너지원으로서 다양한 연구가 진행되고 있다4,5). 이온 교환막 연료전지는 가습된 수소와 산소의 전기 화학반응으로 전기와 물을 생산한다. 이때 공급되는 물과 생성되는 물은 전해막을 통해 양방향으로 이동하며 양극과 전해막의 수분 농도를 유지한다. 하지만 필요 이상의 물이 연료전지 내에 존재하면, 공급기체의 이동을 막고 전기 화학반응을 방해하여 연료전지의 내구성 및 성능을 저하시키며, 충분한 수분이 공급되지 않으면 전해막에 열화가 발생해 내구성 및 수명이 저하된다. 연료전지 성능 및 내구성 향상을 위해 내부 물 관리는 필수적이며 셀 내부의 수분이동에 대한 특성 연구가 필요하다6).
Springer 등7)은 유동채널의 기체 및 수분의 분포를 일정하다 가정하고 전해막 영역에 대한 1차원 해석을 수행하였다. Okada 등8)은 1차원 수분 확산 방정식을 통해 수소이온의 이동에 따른 전해막 내부의 습증기 함유도에 대한 연구를 수행하였다. Yi와 Nguyen9)은 유동채널을 차분화하고 열과 물질전달 방정식을 유도하여 채널흐름에 따른 수분 농도와 분압특성을 연구하였다. Chavan과 Talange10)은 기존 PEMFC의 모델을 Matlab/Simulink® (MathWorks, Natick, MA, USA)를 이용하고 스택 거동을 모사하는 수학적 모델을 제안하였다. Yang 등11)은 1차원적인 해석을 통해 전해막에서의 습증기 함유도를 예측하고 연료전지 성능에 끼치는 영향을 연구하였다.
연료전지의 셀 전압 모델에 관련하여 Sui 등12)은 촉매층을 균일하게 가정하고 전기 화학반응을 모사하여 활성화손실을 계산한 유사 균질(Pseudo-homogeneous) 모델을 제안하였으며, Pukrushpan13)은 연료전지의 공기극에서 발생하는 물질전달손실을 실험식을 통해 나타내었다.
기존의 동특성 모델에서는 전해막의 동적 수분 거동에 대해 보고된 예가 없다. 전해막의 수분 투과 동적 응답이 성능에 중요한 요소이기 때문에, 시스템 수준 연구에서도 전해막의 동적 거동에 대한 응답을 모사하는 것이 필요하다. 본 연구에서는 이온 교환막 연료전지의 동적 부하 가변 환경에서의 수분 농도 변화에 대한특성을 이해하고자 한다.
MATLAB/Simulink® (MathWorks) 플랫폼을 이용해 양극 유동채널 내부의 수분 농도를 계산하여 전해막에서의 비선형 습증기 수송 현상을 모사하는 모델을 개발하고, 동적 작동환경에서 연료극과 공기극의 가습조건, 전해막의 두께 그리고 요구 전류 밀도의 변화에 따른 전해막의 습증기 함유도를 확인하였다. 또한 습증기 함유도에 따른 전해막의 이온 저항과 연료전지의 성능 특성과 응답 특성도 확인하였다.
2. 이온 교환막 연료전지 전해막 비선형 동특성 모델
2.1 수분 수송 모델
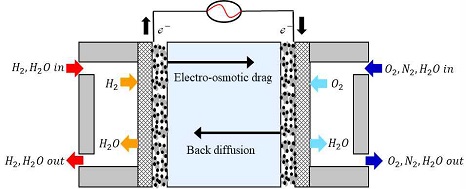
Fig. 1은 고분자 전해질 연료전지 내 수분 이동을 나타낸 그림이다. 연료전지는 연료극, 공기극, 전해막으로 구성되어 있으며, 각 전극으로 공급되는 수소와 공기는 가습된 상태로 공급된다. 연료극에 공급 된 수소는 전해막의 촉매층에서 전기 화학반응을 통해 수소이온과 음이온으로 분해되고, 수소이온은 전해막을 따라 공기극으로 이동한 후, 공기극에 공급 된 산소와 결합하여 물을 생성한다.
양극의 수분 농도는 연료전지 분리판 유로를 통과하는 기체의 물 분율로 나타낼 수 있으며, 입출구의 물 농도와 전해막을 따라 이동하는 습증기의 유동으로 결정된다. 실제 연료전지 구동에 있어서 양극의 물 분율은 공급 기체가 분리판 유로를 이동하며 변하지만, 본 연구에서는 연료전지의 1차원 해석을 통해 전해막의 함습도 특성을 확인하는 것이 목표이기 때문에, 분리판 유로에 존재하는 기체의 물 분율은 위치에 관계없이 동일하다 가정하고 해석을 진행하였다.
| (1) |
| (2) |
전기 화학반응 이후 배출되는 물의 농도는 양극에서 최종적으로 배출되는 기체의 몰과 식 (1)과 식 (2)에서 계산된 물 분율로 나타낼 수 있다.
| (3) |
| (4) |
| (5) |
전해막을 따라 이동하는 습증기의 유동은 두 가지 구동력의 균형으로 결정된다. 즉, 수소이온에 의한 전기삼투력과, 양 단 수분 농도차에 의한 역확산력이다. 두 가지 구동력 이외에도 양 전극에서의 압력차로 인한 습증기 이동도 존재하지만 본 연구에서는 양 전극의 압력차는 동일하다고 가정하였다. 따라서 전해막의 수분 수송의 지배 방정식은 전기삼투력과 역확산력 균형으로부터 유도되며, Yu와 Jung14)이 제안한 비정상 종보존 방정식을 통해 나타낼 수 있다.
| (6) |
전해막의 전기 전도도는 막 내부의 습증기 농도에 따라 민감하게 반응하므로, 전해막 내부 습증기의 농도를 적절히 관리하는 것이 연료전지의 성능에 중요하다. Springer 등7)은 습증기 함유도(water content)라는 개념을 사용하여 전해막의 습증기 농도를 나타내었으며, 이를 통해 전해막의 물 확산계수 상관식을 제안하였다. 또한 전해막의 전기삼투압계수도 습증기 함유도로 나타낼 수 있는데, 본 연구에서는 Dutta 등15)이 제안한 식을 모델에 적용하였다.
| (7) |
| (8) |
| (9) |
식 (6)과 식 (7)을 통해 전해막 내부의 습증기 함유도는 식 (10)으로 나타낼 수 있다.
| (10) |
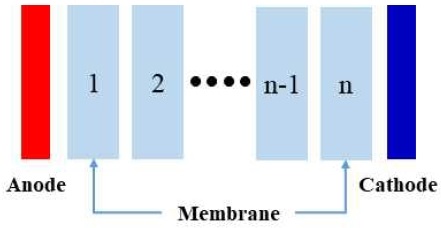
전해막의 비선형 습증기 수송현상을 모사하기 위해선 습증기 함유도를 통해 전해막 내부의 수분 분포 경향을 확인하여야 한다. 따라서 본 연구에서는 Fig. 2와 같이 전해막을 n개의 노드로 차분화 후, 식 (10)으로부터 다음과 같은 식을 도출하였다.
| (11) |
식 (11)의 경계 조건은 다음과 같다.
| (12) |
양극의 습증기 함유도는 수분활성도를 통한 경험식으로 나타낼 수 있으며7), 수분활성도는 식 (4)과 식 (5)로 계산된 물 분율을 통해 계산할 수 있다.
| (13) |
| (14) |
전해막의 전기 전도도는 식 (11)을 통해 계산된 각 노드별 습증기 함유도를 실험식에 적용하여 계산하였다1).
| (15) |
전해막의 전체 전기저항은 식 (15)를 통해 계산된 각 노드별 전기 전도도를 적분한 후, 총합으로 나타내었다.
| (16) |
2.2 전압 모델
연료전지의 실제 전압은 전기 화학반응으로 발생하는 이론적인 전압으로부터 손실들을 모두 고려하여 구하여 한다. 실제 작동 전압은 다음과 같이 나타낼 수 있다.
| (17) |
연료전지가 기전력은 Nernst에 의해 제안된 상관식을 통해 구하였다.
| (18) |
이온 교환막 연료전지의 전기 화학반응은 양극의 촉매층에서 발생하며 화학반응의 속도가 느리기 때문에 발생된 전압의 일부분이 전기 화학 반응에서 손실된다. 그러나 연료극에서 수소 산화 반응은 공기극에서의 산소 소모 반응보다 훨씬 빠르므로 활성화 손실은 공기극에서만 고려된다. 본 연구에서는 공기극의 전기 화학반응 모델링하기 위해 Sui 등12)이 제안한 Pseudo-homogeneous 모델의 전기 화학반응식을 적용하였다.
| (19) |
전해막에서의 이온 전달 손실은 식 (16)을 통해 계산된 전기저항을 통해 구해진다.
| (20) |
마지막으로 물질 전달 손실은 환원반응을 통해 물이 생성되는 공기극에서 발생하며 생성된 물로 인해 공기극의 물 농도가 높아져 산소의 전기 화학반응을 방해하여 전압 손실을 일으킨다. 본 연구에서는 Pukrushpan13)이 제안한 실험식을 사용하여 모델링을 하였다.
| (21) |
| (22) |
| (23) |
모델링에 사용한 모든 수식의 parameter 및 작동 조건을 Table 1에 나타내었다.
3. 결과 및 고찰
본 연구에서는 이온 교환막 연료전지의 양극의 가습 조건에서의 입구조건에 따른 전해막 습증기 함유도 및 성능 특성을 시뮬레이션을 통해 확인하고자 하였으며, 시뮬레이션 결과는 모델이 정상상태에 도달하였을 때의 데이터를 기반으로 비교하였다. 특별한 언급이 없는 경우 기준 파라메터는 Table 1을 이용하였으며, 전해막의 두께는 25 μm와 108 μm로 나누어 비교하였다.
3.1 연료전지 셀 모델 검증
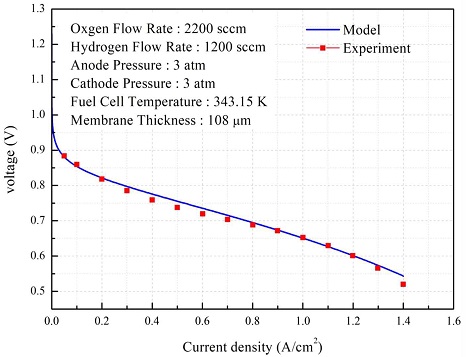
연료전지 비선형 동특성 모델을 Wang 등16)이 실험 및 모델링한 결과와 비교하여 검증하였다. 셀 구동 온도는 70°C로 유지시켰으며 압력은 300 kpa이다. 그 이외의 parameter는 Fig. 3에 나타내었다. 모델과 문헌상 결과를 비교하면 0.996566의 상관계수(R)를 보이며 일반적으로 알려진 연료전지 운전 구간에서 적절히 수렴하고 있는 것을 볼 수 있다.
3.2 전류밀도별 전해막 습증기 함습도
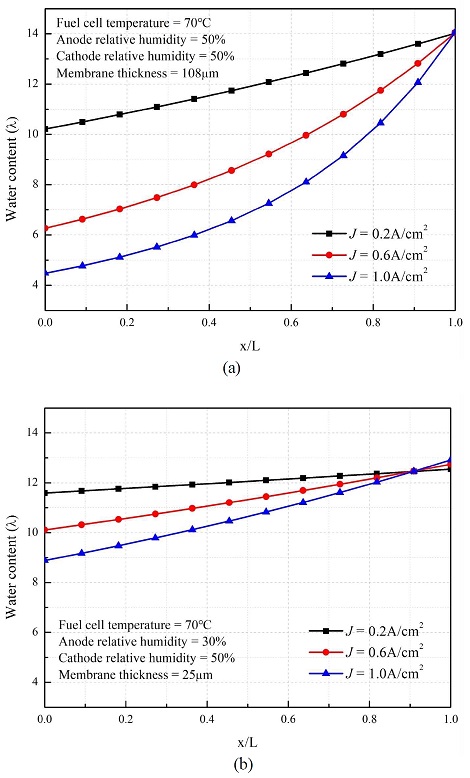
Fig. 4는 전류밀도의 크기에 따라 전해막 내부의 습증기 함유도를 나타낸 그림이다. 셀의 온도는 70℃를 유지하였으며, 기체의 압력은 100 kpa로 공급해 주었다. 두께는 108 μm인 전해막을 사용하였고, 공기극 가습량은 50%, 연료극 가습량은 각각 50%와 30%로 공급하였다. 두 그림 모두 공기극과 연료극의 습증기 함유도 차이에 따라 전해막 내부의 습증기 함유도가 비선형적으로 증가함을 나타낸다. Fig. 4(a)는 연료극 가습을 50%로 공급하였을 때의 습증기 함유도 분포를 나타내는 그림이다. 공기극의 습증기 함유도는 환원반응으로 생성된 물과 전기삼투력으로 수송된 물로 인해 전류밀도에 관계없이 일정한 값을 유지하는 것을 확인할 수 있다. 허나 연료극의 습증기 함유도는 전류밀도의 증가에 따라 감소하는 것을 확인 할 수 있는데, 이는 전류밀도가 증가할수록 전기 화학반응이 활발하게 이루어져 전기삼투력이 강해지고, 이 때문에 수소이온이 물을 공기극으로 더 많이 수송하게 되어 연료극의 습증기 함유도가 감소하게 됨을 나타낸다. 전기삼투력으로 인해 양극의 함습도 차이는 커지게 되지만, 그로인해 역확산력 또한 강해지게 되어 두 개의 반대되는 힘은 평형을 이루게 되고, 전해막은 열화 되지 않고 수분 농도를 적절히 유지할 수 있다. Fig. 4(b)는 연료극 가습량을 30%로 공급하였을 때의 습증기 함유도를 나타내는데, 일정 전류밀도 이상에서 공기극의 습증기함유도가 일정한 값을 유지하는 것을 확인할 수 있다. 이는 연료극의 낮은 가습량으로 인해 역확산력이 강해져 공기극의 물이 연료극으로 이동하게 되지만, 전류밀도가 증가할 때 환원반응이 증가하여 일정 전류밀도 이상에선 생성된 물로부터 충분한 수분을 공급받아 일정 습증기 함유도를 유지할 수 있음을 나타낸다.
Profiles of water content across nafion 115 membrane at different operating condition (a) anode relative humidity 50% (b) anode relative humidity 30%
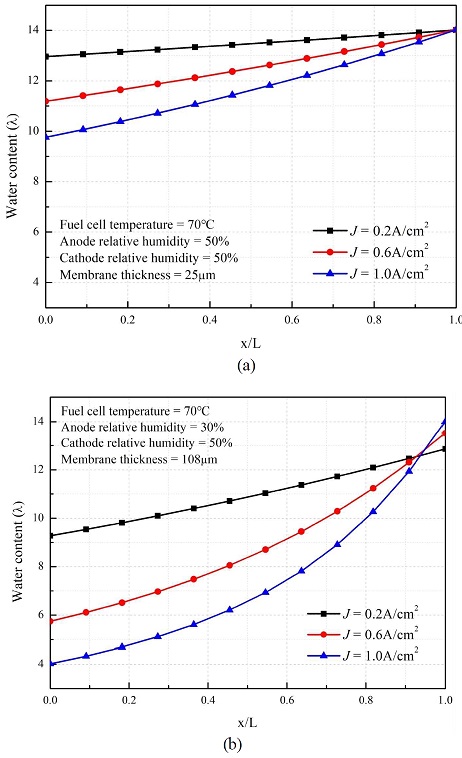
Fig. 5는 두께가 25 μm인 전해막을 사용하였고 다른 조건은 Fig. 4의 조건과 동일하다. Fig. 5에서 전해막의 두께가 감소하여 각 노드의 습증기 함유도가 증가하고, 전류밀도별 습증기 함유도 분포 차이가 감소함을 보이고 있다. 전해막 두께의 감소는 역확산력을 강하게 만들어 연료극으로 흘러가는 물의 양을 증가시키고, 그로인해 연료극의 습증기 함유도가 전해막이 두꺼울 때보다 증가하게 된다. Fig. 5(a)는 연료극 가습을 50%로 가습하였을 때의 습증기 함유도 분포를 나타낸 그림이다. Fig. 4(a)과 달리 그래프가 선형적인 모습을 보이는데, 이는 수분활성도가 높은 구간에선 습증기 함유도가 선형적으로 증가하기 때문이다. Fig. 5(b)는 연료극 가습을 30%로 가습하였을 때의 습증기 함유도 분포를 나타내 그림이다. 공기극 습증기 함유도가 최댓값에 도달하지 못해 일정하게 유지하지 않고 계속 증가하는 것을 확인할 수 있다. 역확산력으로 흘러간 물로 인해 공기극의 습증기 함유도가 감소하였고, 환원반응으로 생성된 물로 수분을 충분히 공급받지 못해 증기 함유도의 최댓값까지 지속적으로 증가함을 알 수 있다.
3.3 전해막 두께별 이온 저항
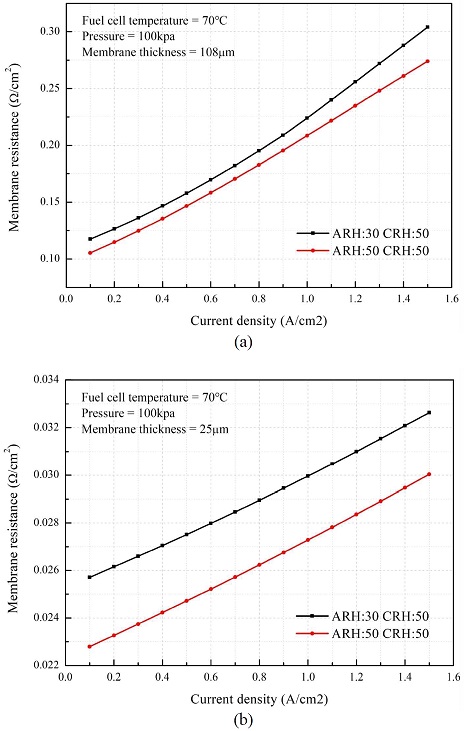
Fig. 6은 전해막 두께별 이온 저항을 나타낸 그림이다. 전해막의 두께가 두꺼울수록 막 내 전체적인 습증기 함유도가 낮아 각 노드별 이온 전도도가 감소하고, 수소이온의 이동거리가 증가하여 전체 이온 저항이 높아지는 것을 확인할 수 있다. 또한 습도별 이온 저항도 두께가 두꺼울수록 큰 차이를 보였는데, 이는 전기저항을 계산할 때 전기 전도도의 역수를 곱하기 때문에 발생한다. 두께가 두꺼운 전해막은 각 노드별 이온 전도도가 낮고 역수를 취한 값이 커 이온 전도도 상승에 따른 이온 저항의 감소폭이 크고, 얇은 전해막은 각 노드별 이온 전도도가 높고 역수를 취한 값이 작아 이온 전도도 상승에 따른 이온 저항의 감소폭이 작다. 이를 통해 전해막의 두께가 두꺼울수록 이온 전도도가 낮고 이온 저항이 습도 변화에 민감하게 반응함을 확인할 수 있다.
3.4 전해막 두께별 성능곡선
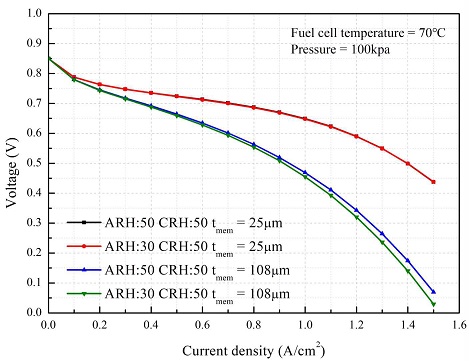
Fig. 7은 전해막 두께별 연료전지 성능곡선을 나타낸 그림이다. 앞선 연구에서 연료극 가습량을 30%에서 50%로 증가시켰을 때 전해막 두께별 습증기 함유도 특성 및 이온 저항의 변화를 확인할 수 있었고, 그에 따른 연료전지 전압성능을 확인하기 위해 동일조건으로 공기극의 상대습도는 50%, 연료극 상대습도는 30%에서 50%로 증가시켰다. 전해막의 두께가 두꺼울 경우 이온 저항이 증가하여 얇은 전해막에 비해 성능이 낮은 것을 확인할 수 있다. 또한 두꺼운 전해막의 경우 가습량 감소에 따른 이온 저항의 증가 폭이 커 연료전지 성능이 얇은 전해막에 비해 가습량 변화에 민감하게 반응함을 확인할 수 있다. 따라서 효과적으로 연료전지를 운전하기 위해서는 전해막 두께별로 운전조건을 다르게 가져가야하는데, 두께가 두꺼울 경우 양극의 가습량을 조절하여 전해막 내부를 충분히 수화시켜 이온 저항을 줄이는 조건으로 연료전지를 운전해야 하며, 두께가 얇을 경우 가습량 변화가 전해막의 전기저항에 큰 영향을 주지 않으니 전해막이 열화되지 않을 정도의 가습량을 공급하여 가습기로 인한 전력소비를 줄이는 운전조건을 채택하는 것이 바람직한 것으로 판단된다.
4. 결 론
이온 교환막 연료전지의 비선형 동특성 모델을 개발하여 전해막 내부의 습증기 함유도 분포를 분석하였다. 연료전지의 운전변수로 연료극의 상대습도와 전해막 두께를 고려하여 전해막 내부의 습증기 함유도, 이온 저항 그리고 연료전지의 성능을 계산하여 비교 분석하였으며 주요 결과는 다음과 같이 요약할 수 있다.
1) 공기극 습증기 함유도는 연료극 가습량에 영향을 받으며, 연료극 가습량이 50%인 경우 요구 전류밀도가 0.2 A/cm2 이상인 구간에서 정상상태에 도달하지만, 연료극 가습량이 30%인 경우 요구 전류밀도가 1 A/cm2 이상인 구간에서 정상상태에 도달한다.
2) 연료극 가습량이 30%일 때, 전해막 두께가 25 µm인 경우, 막 내 전체적인 습증기 함유도는 전해막 두께가 108 µm인 경우보다 증가하지만, 전해막 두께의 증가에 따라 역확산력이 강해져 공기극 습증기 함유도는 정상상태에 도달하지 못한다.
3) 연료극 가습량 감소에 따른 연료전지 전압성능은 전해막이 두께가 108 µm인 경우 최대 0.05 V 감소를 보였고, 전해막이 두께가 25 µm인 경우 최대 0.0005 V 감소하며 전압성능이 거의 감소하지 않는 모습을 보였다.
4) 요구 전류밀도가 0.1 A/cm2일 때와 1.5 A/cm2일 때의 이온 저항 차이는 전해막 두께가 108 µm인 경우 0.2 Ω/cm2로 큰 차이를 보였으며, 전해막 두께가 25 µm인 경우 0.07 Ω/cm2로 미미한 감소를 보였다.
본 모델을 통해 연료전지 정상상태에서의 습증기함유도 특성을 확인하였고, 추가적으로 비정상상태를 고려하면 습증기 함유도의 동특성 해석이 가능할 것으로 기대된다.
Acknowledgments
본 연구는 산업통상자원부(MOTIE)와 한국에너지기술평가원(KETEP)의 지원(No. 20203010030010)과 2021년도 산업통상자원부 및 산업기술평가관리원(KEIT) 연구비 지원(20011907)에 의한 연구입니다.
References
-
X. Cheng, Z. Shi, N. Glass, L. Zhang, J. Zhang, D. Song, and J. Shen, “A review of PEM hydrogen fuel cell contamination: impacts, mechanisms, and mitigation”, J. Power Sources, Vol. 165, No. 2, 2007, pp. 739-756.
[https://doi.org/10.1016/j.jpowsour.2006.12.012]

-
S. Kélouwani, K. Agbossou, and R. Chahine, “Model for energy conversion in renewable energy system with hydrogen storage”, J. Power Sources, Vol. 140, No. 2, 2005, pp. 392-399.
[https://doi.org/10.1016/j.jpowsour.2004.08.019]

-
L. Carrette, K. A. Friedrich, and U. Stimming, “Fuel cells: principles, types, fuels, and applications”, ChemPhysChem, Vol. 1, No. 4, 2000, pp. 162-193.
[https://doi.org/10.1002/1439-7641(20001215)1:4<162::AID-CPHC162>3.0.CO;2-Z]

-
N. Z. Muradov and T. N. Veziroğlu, ““Green” path from fossil-based to hydrogen economy: an overview of carbon-neutral technologies”, Int. J. Hydrog. Energy, Vol. 33, No. 23, 2008, pp. 6804-6839.
[https://doi.org/10.1016/j.ijhydene.2008.08.054]

-
M. Steinberg, “Fossil fuel decarbonization technology for mitigating global warming”, Int. J. Hydrog. Energy, Vol. 24, No. 8, 1999, pp. 771-777.
[https://doi.org/10.1016/S0360-3199(98)00128-1]

-
J. Son, J. Jeong, and S. Yu, “Measurement of diffusion coefficient and water transport flux in Nafion® 117 membrane”, The Korean Society of Mechanical Engineers, Vol. 43, No. 9, 2019, pp. 631-637.
[https://doi.org/10.3795/KSME-B.2019.43.9.631]

-
T. E. Springer, T. A. Zawodzinski, and S. Gottesfeld, “Polymer electrolyte fuel cell model”, J. Electrochem. Soc., Vol. 138, No. 8, 1991, pp. 2334-2342.
[https://doi.org/10.1149/1.2085971]

-
T. Okada, G. Xie, and M. Meeg, “Simulation for water management in membranes for polymer electrolyte fuel cells”, Electrochimica Acta, Vol. 43, 1998, No. 14-15, pp. 2141-2155.
[https://doi.org/10.1016/S0013-4686(97)10099-8]

-
J. S. Yi and T. V. Nguyen, “An Along-the- channel model for proton exchange mem- brane fuel cells”, Journal of the Electrochemical Society, Vol. 145, No. 4, 1998, pp. 1149-1159.
[https://doi.org/10.1149/1.1838431]

-
S. L. Chavan and D. B. Talange, “Modeling and performance evaluation of PEM fuel cell by controlling its input parameters”, Energy, Vol. 138, 2017, pp. 437-445.
[https://doi.org/10.1016/j.energy.2017.07.070]

- J. S. Yang, G. M. Choi, and D. J. Kim, “Prediction of fuel cell performance and water content in the membrane of a proton exchange membrane fuel cell”, The Korean Society of Automotive Engineers, Vol. 14, No. 6, 2006, pp. 151-159. Retrieved from https://www.dbpia.co.kr/journal/articleDetail?nodeId=NODE00770118, .
- P. C. Sui, L. D. Chen, J. P. Seaba, and Y. Wariishi, “Modeling and optimization of a PEMFC catalyst layer”, SAE Technical Paper Series, 1999.
- J. T. Pukrushpan, “Modeling and control of fuel cell systems and fuel processors”, University of Michigan, 2003. Retrieved from http://www-personal.umich.edu/~annastef/FuelCellPdf/pukrushpan_thesis.pdf, .
-
S. Yu and D. Jung, “Thermal management strategy for a proton exchange membrane fuel cell system with a large active cell area”, Renewable Energy, Vol. 33, No. 12, 2008, pp. 2540-2548.
[https://doi.org/10.1016/j.renene.2008.02.015]

-
S. Dutta, S. Shimpalee, and J. W. Van Zee, “Numerical prediction of mass-exchange between cathode and anode channels in a PEM fuel cell”, International Journal of Heat and Mass Transfer, Vol. 44, No. 11, 2001, pp. 2029-2042.
[https://doi.org/10.1016/S0017-9310(00)00257-X]

-
L. Wang, A. Husar, T. Zhou, and H. Liu, “A parametric study of PEM fuel cell performances”, Advanced Energy Systems, 2002, pp. 139-145.
[https://doi.org/10.1115/IMECE2002-33167]