수소 저장용 탱크의 튜브 형상에 따른 온도분포 특성에 대한 수치해석 연구
2021 The Korean Hydrogen and New Energy Society. All rights reserved.
Abstract
Recently, it is necessary for study on renewable energy due to environmental pollution and fossil fuel depletion. Therefore, in this study, the filling temperature according to the nozzle geometry was evaluated based on the limit temperature specified in SAEJ2601 for charging hydrogen, a new energy. There are three types of nozzles, normal, angle and round, fixed the average pressure ramp rate at 52.5 MPa/min, and the injection temperature was set at 293.4 K. As a result, the lowest temperature distribution was found in the round type, although the final temperature did not differ significantly in the three types of nozzles. In addition, Pearson's coefficient was calculated to correlate the mass flow rate with the heat transfer rate at the inner liner wall, which resulted in a strong linear relationship of 0.98 or higher.
Keywords:
Hydrogen, Hydrogen storage vessel, Numerical analysis, Pressure, Temperature키워드:
수소, 수소 저장 용기, 수치해석, 압력, 온도1. 서 론
최근 환경오염 문제로 인해 신재생에너지 및 대체연료에 대한 연구가 활발히 진행되고 있다. 기존에 사용되는 연료 중 가장 큰 문제가 되고 있는 디젤의 경우, 가솔린 연료와 비교하여 연비가 좋고 불완전연소가 적은 등의 장점이 있지만 배기가스 배출량에서 입자상물질(particlulate matter)과 질소산화물(nitrogen oxide, NOx)이 높아 문제가 심각1)하며 이를 해결하기 위해 전처리 및 후처리 기술에 대한 연구가 진행되고 있다2). 또한 추가적인 장치 없이 기존의 연료에 그 외의 물질(식물성 기름, 물 등의 친수성 물질)을 첨가하여 비율을 조절함으로 연료 자체의 사용을 감소시키거나 물성치 차이에 기인한 연소실 온도감소 및 미세폭발(micro-explosion)로 NOx 및 Soot를 감소시킬 수 있는 연구가 진행 중이다3). 이러한 방법이 적용된 연료는 바이오디젤(biodiesel)4), 에멀젼 연료(emulsified fuel)1) 등이 있다.
하지만 부가적인 장치 및 연료설계를 통한 방법들은 화석연료를 기반으로 하고 있어 본질적인 문제해결 방법이 아니다. 현재 유럽연합(European Union, EU)과 미국은 탄소 국경세 도입을 논의 중이며, EU의 경우 자동차 배출가스 규제 상향 등을 추진하고 있다. 이에 한국 정부는 탄소중립 추진전략을 경제구조 모든 영역에 적용하여 에너지 주공급원인 화석연료에서 깨끗한 신재생에너지로의 추진을 제도화하였다5). 따라서 기존 화석연료를 기반한 개선 방법은 한계가 있고 대체 에너지에 대한 연구 및 도입이 필요하다. 화석연료를 대체하기 위한 방법으로 배터리 기반의 전기차와 수소와 산소의 전기화학반응을 통해 생선된 전기로 모터를 구동하는 수소전기차가 있다.
특히, 신에너지인 수소는 온실가스 배출이 없고 물, 유기물 등의 화합물로부터 제조할 수 있고 화석연료의 경우 특정 지역에 매립되어 지정학적으로 문제가 있지만 이와 비교하여 수소의 경우 지역적 편중이 없다. 수소전기차는 전기차와 비교하여 에너지밀도가 높고 충전 시간이 적다는 등의 장점이 있다6). 이를 위해서는 수소저장탱크의 일정한 내구성과 안전성이 확보되어야 하며, 관련 분야에 대한 많은 연구가 진행되고 있다.
일반적으로 고압으로 충전되는 수소기체에서 이상기체(ideal gas) 방정식의 적용은 적절하지 못하며 3차 상태방정식(cubic equations of state [EOS])이 널리 적용되고 있다. 이에 Park7)은 수소 충전에서 3차 상태 방정식 중 van der Waals 상태방정식(vdW EOS), Redlich-Kwong 상태방정식(RK EOS), Soave-Redlich-Kwong 상태방정식(SRK EOS) 및 Peng-Robinson 상태방정식(PR EOS)을 적용하여 수소 충전을 모사하였다. Dicken과 Mérida8)는 2D 축대칭(axistmmetry)을 적용하여 충전 시간 40 s, 35 MPa 및 74 L 부피를 가지는 탱크에서 실험데이터와 수치해석 데이터를 비교하여 내부 평균 온도가 2.2 K 이내에서 일치하는 결과를 보고하였다.
Lee 등6)은 수소의 잔존 용량(state of charge, SOC)에 따라 –40℃, 40 g/s의 일정유량조건하에서 수소 탱크에 수소를 충전하였을 때 나타나는 열적 특성을 연구하였으며 SOC가 많을수록 충전 시간은 단축되며 초기온도에 비해 최종온도는 증가하는 것을 확인하였다. 또한 Suryan 등9)은 수소 탱크 충전모사 해석에서 난류 모델에 따른 수치해석 결과를 실험데이터와 비교하여 수소 충전 모사를 위한 적합한 난류 모델이 realizable k-ε model and the Reynolds Stress model이라고 보고하였다.
수소 충전에서 작동 조건에 따른 연구 결과는 보고되고 있지만 저장용기에 삽입되어 있는 튜브 형상이 수소 충전 시 온도 분포 및 압력 증가에 미치는 영향에 대한 분석 및 연구가 국내외적으로 미미하므로 이에 대한 연구가 필요한 시점이다.
따라서 본 연구에서는 튜브 형상 변화에 대한 수소 저장용 탱크의 온도 분포 특성 및 충전 시간에 대해 수치 해석적으로 연구하였다. 튜브 끝단의 노즐을 총 3가지 형상으로 구분하여 해석을 진행하였으며 수치기법이 적합한지를 판단하기 위해 선행 연구8)의 실험 결과와 비교하여 수치해석 기법을 검증하고 노즐 형상에 따른 수소 충전 특징에 대해 분석하였다.
2. 수치해석 방법
2.1 지배방정식 및 실제 기체 방정식
본 연구에서 수소 충전을 모사하기 위해 유한체적법(finite volume method) 기반의 ANSYS (Canonsburg, PA, USA) Fluent 2020 R2를 적용하였으며 지배 방정식은 다음과 같다10).
-The continuity equation
| (1) |
-Momentum conservation equation
| (2) |
-Energy conservation equation
| (3) |
여기서 t, ρ는 각각 시간과 밀도를 나타내고 v, p, s는 속도 벡터, 정압 및 소스항을 나타낸다. 는 응력 텐서를 의미하고 다음과 같다.
| (4) |
여기서 μ는 점성계수를 I는 단위 텐서이다.
수식 (3)에서 E = h - (p/ρ) + (1/2)v2이고 유효열전도율 kgeff = kg + kt에서 kt = (cpgμt) / Prt이며 Prt는 난류 Prandtl 수이다. 는 점성가열을 나타낸다.
수소의 탱크 충전 과정에서 변화하는 온도, 압력 및 체적 등의 물리적 특성을 예측하기 위해서는 조건에 적합한 상태방정식(EOS)을 적용해야한다. 일반적으로 사용되는 이상기체 방정식(ideal gas equation)은 수소 충전과 같은 상대적으로 밀도가 크고 고압의 조건에서는 적합하지 않다7). 따라서 실제 기체 방정식(real gas equation)을 적용해야하며 대표적으로 van der Waals' Gas Equation이 있다. 하지만 선행 연구11)의 결과를 바탕으로 Redlich and Kwong 방정식을 적용하였으며 상태 방정식은 다음과 같다.
| (5) |
여기서 a, b는 다음과 같이 구해진다.
| (6) |
| (7) |
2.2 수치해석 방법
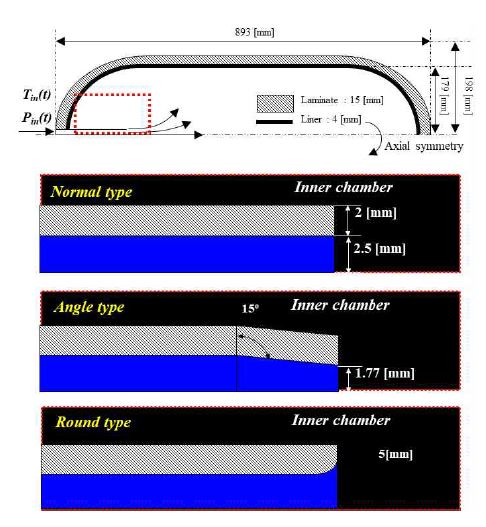
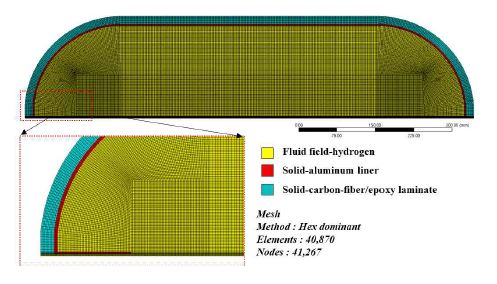
노즐 형상에 따른 수소 탱크 충전 해석을 진행하기 위해 Fig. 1과 같이 수소 탱크를 모델링 하였다. 해석에 적용된 수소 탱크는 Type III으로 자세한 치수 정보는 Table 1에 나타내었고 수소 탱크의 용량은 74 L이다. 수소 탱크에 충전 튜브의 형상을 Fig. 1에 그림과 같이 직관 형상의 normal type, 직관형상에서 내부 15o로 기울어진 형태로 면적비 1:2로 설정한 angle type과 반지름 5 mm로 라운드 형태의 round type으로 설정하였다. 각각의 노즐을 통해 유입되는 수소 온도는 293.4 K로 고정하였고 평균압력상승속도(average pressure ramp rate, APRR)를 52.5 MPa/min로 설정하였다. 초기 탱크 내부 온도 및 압력은 각각 25℃, 0 atm으로 설정하였다. 해석에 적용된 모델은 해석 소요 시간 등을 고려하여 2D 축대칭(axisymmetry)으로 설정하였으며 Fig. 2는 격자 형상을 나타낸다. 격자는 형상은 정렬격자인 Hex dominant 격자 및 노드 수는 각각 57,632 및 58,128이다. 적용된 Fluent의 해석 솔버는 coupled scheme을 적용하였고 난류 모델로는 선행 연구에서 수소기체 충전에 적합하다고 알려진 Realizable k-epsilon을 적용하였다. 대기 온도는 293.4 K 및 외부 대류 계수는 10 W/m2K으로 설정하였다.
3. 결과 및 고찰
3.1 수치해석 검증
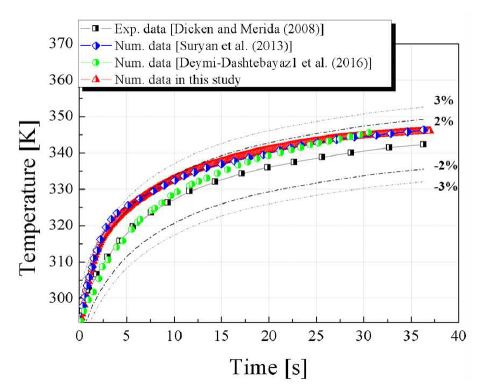
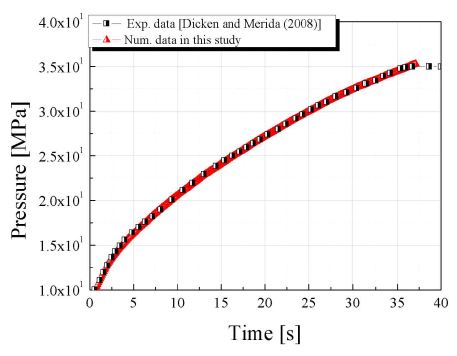
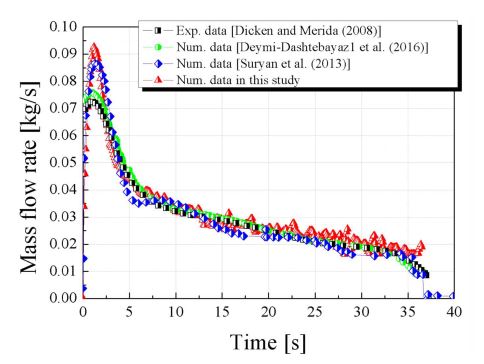
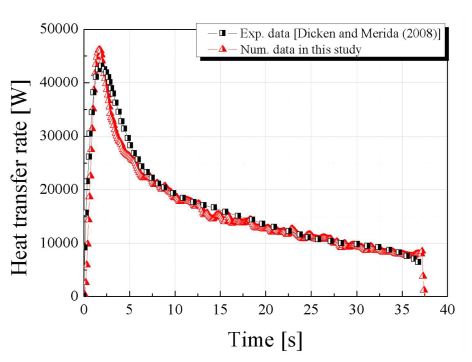
수치해석을 실시하기 전, 본 연구에서 적용된 난류 모델 및 real gas model (Redlich-Kwong equation)이 실제 수소 탱크의 충전을 모사하는 데 적합한지를 검증하기 위해 선행 연구 결과8,9)를 참고하여 동일조건에서 해석을 실시하였고 이를 각각의 연구에서 실험 및 수치해석 결과와 비교하였다. 검증을 위해 실시한 해석의 경계조건은 Table 2에 나타낸다. 입구 경계 조건은 수소기체의 압력과 온도의 실험데이터를 활용하였다. Fig. 3은 수소 탱크 내의 평균 온도를 시간에 따라 나타낸 결과이며 Fig. 4와 같이 각 시간에 대해 수소저장용기의 평균 온도로 구하였다. 그래프와 같이 선행 연구의 결과인 실험 데이터와 수치해석 데이터를 비교하였을 때 평균 온도 데이터의 오차율은 2%임을 확인 할 수 있다. 또한 Figs. 5-7은 각각 수소 저장 용기 내부 평균 압력 변화 및 노즐 입구에서 질량 유량 및 내부 벽면에서의 열전달률의 결과를 나타낸 것으로 그림과 같이 시간 변화에 따른 평균 압력과 질량 유량 및 열전달률의 경향이 선행 연구와 유사한 것을 확인할 수 있다. 이러한 결과 역시 시간에 따른 평균온도 변화와 비교하였을 때 그 경향성이 실험과 유사한 것을 확인할 수 있으며 노즐 형상 변화에 따른 수소 저장용 탱크의 해석을 실시하기 위해 동일기법을 적용하였다.
3.2 노즐 형상에 따른 수치해석 결과
노즐 형상 및 질량 유량에 따른 수소 저장 탱크의온도 및 압력 분포 특성을 분석하기 위해 선행 연구와 비교하여 검증된 수치해석 기법을 바탕으로 변수에 따른 해석을 실시하였다.
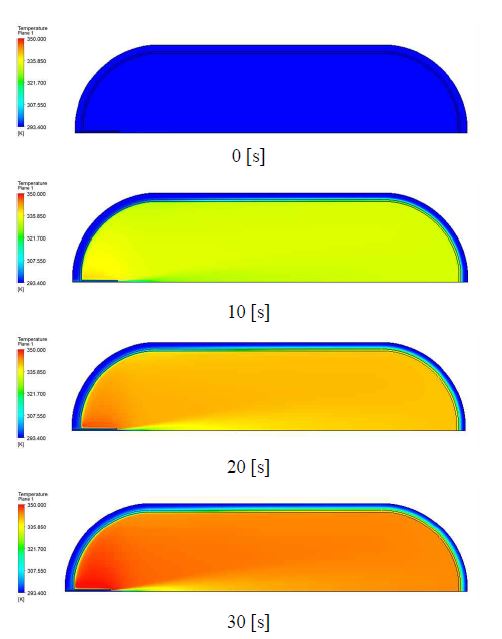
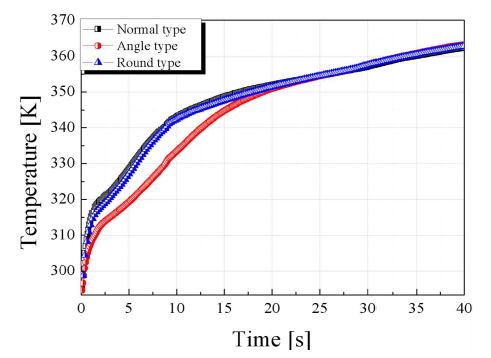
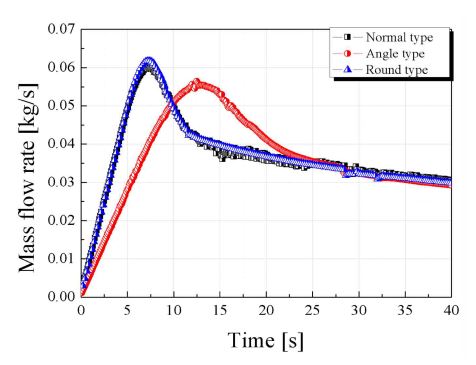
온도 293.4 K, APRR 52.5 MPa/min 조건에서의 경우 그림과 같이 normal type, angle type 및 round type에서 Fig. 8과 같이 충전 시간 40 s에서 약 360 K의 온도 분포를 확인할 수 있다. Normal 및 round type의 경우 그림과 같이 수소 저장 용기 내부 온도 상승 경향이 비슷하지만 angle type의 경우 15 s까지 낮은 상승률을 보인다. 그후부터는 normal, round type과 비슷한 증가율을 보인다. 이는 초기 압력 상승에 따라 angle type의 경우 노즐 형상으로 인해 저항이 증가하여 나타나는 형상으로 판단되며 이는 Fig. 9의 유량 증가와 동일하다. 특히, 최종 충전 시간 40 s에서 normal, angle 및 round type에서 최종 온도는 각각 362.912424, 363.2196 및 362.75598 K으로 미소하지만 round type의 경우가 낮은 온도 분포를 확인 할 수 있다. Angle type의 경우 질량 보존에 따른 입구가 좁은 노즐 홀에서 속도 증가로 직관의 경우보다 상대적으로 압축비가 높아지고 이에 따라 열발생이 증가고 줄-톰슨효과(Joule-Thomson effect)에 의한 온도 상승이 이유인 것으로 판단된다. 또한 노즐 형상에 따른 명확한 결과를 확보하기 위해서는 APRR의 변경에 따른 열적 특성이 필요하다고 판단된다.
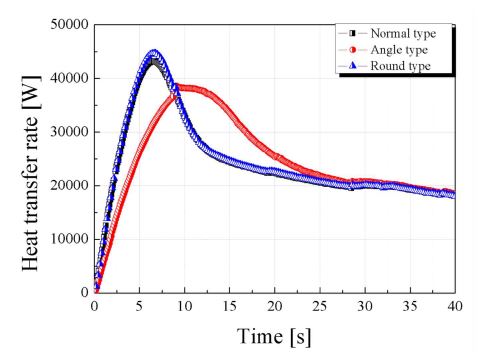
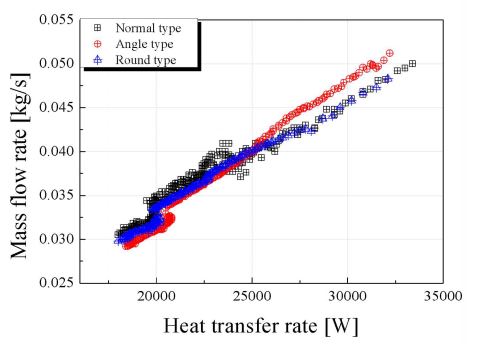
내부 liner 벽면에서의 열전달률을 확인해보면 Fig. 10에서 나타난 바와 같이 전체적으로 유량 결과와 유사한 경향을 확인할 수 있다. 이러한 결과는 수소 저장 용기로 유입되는 기체 수소의 속도는 저장용기 내의 속도장과 난류 운동 에너지의 크기에 직접적인 영향을 미치며, 내벽과의 대류 계수를 통한 열 전달률에 영향을 주기 때문에 흡입 유량이 클수록 대류 계수의 증가량이 상승한다. Fig. 9의 유량 결과와 Fig. 10의 열전달률 결과를 확인해 보면 유량이 상승하는 부분과 열전달률이 상승하는 시간대가 동일한 시점에 발생하며 데이터의 형태가 유사한 것을 확인 할 수 있다. 따라서 유량과 열전달률은 상관관계가 있는 것으로 판단된다. Fig. 11은 이러한 관계를 분석하기 위해 나타낸 결과이며 x축은 열전달률, y축은 유량을 나타낸다. 통계적 분석 방법(Pearson's r Correlation)을 통해 상관계수12)를 도출하면 normal, angle 및 round type의 경우에서 각각 0.9723, 0.99468 및 0.98588로 강한 선형관계를 나타내는 것을 확인할 수 있다.
4. 결 론
본 연구는 노즐형상에 따른 수소 저장용기 충전 특성을 온도, 유량, 내부 벽면에서의 열전달률 등을 통해 분석하였다. 그 결과는 다음과 같다.
1) 선행 연구의 실험데이터를 바탕으로 수치해석적으로 모사하기 위해 실제 기체방정식을 적용하였으며 실험데이터와 2% 오차 이내에서 모사 가능함을 확인하였다.
2) 노즐 형상 normal, angle 및 round type에서 최종 온도는 약 360 K으로 동일하며 angle type의 경우 기하학적 특성으로 인해 저항이 증가하여 초기 15 s까지 온도 상승률은 낮았다.
3) 유량과 내부 벽면에서의 열전달률의 선형관계를 분석하기 위해 통계학에 기초한 Pearson coefficient를 도출하였고 노즐 형상과 무관하게 0.97 이상의 강한 선형관계를 확인할 수 있었다.
노즐 형상 변화에 따른 수소 충전용기의 열적 특 분석에 있어 기초자료로 활용될 수 있을 거라 기대된다.
Acknowledgments
이 논문은 동아대학교 교내연구비 지원에 의하여 연구되었습니다.
References
-
J. K. Yeom and J. H. Yoon, “Study of behavior characteristics of emulsified fuels with evaporative field”, Trans. Korean Soc. Mech. Eng. B, Vol. 39, No. 3, 2015, pp. 237-243.
[https://doi.org/10.3795/KSME-B.2015.39.3.237]

-
J. K. Yeom and J. H. Yoon, “Basic study of spray-behavior characteristics of emulsified fuel”, Trans. Korean Soc. Mech. Eng. B, Vol. 38, No. 9, 2014, pp. 763-771.
[https://doi.org/10.3795/KSME-B.2014.38.9.763]

-
M. Huo, S. Lin, H. Liu, and C. F. Lee, “Study on the spray and combustion characteristics of water-emulsified diesel”, Fuel, Vol. 123, 2014, pp. 218-229.
[https://doi.org/10.1016/j.fuel.2013.12.035]

-
S. Y. No, “Application of bio-oils from lignocellulosic biomass to transportation, heat and power generation-a review”, Renew Sustain Energy Rev., Vol. 40, 2014, pp. 1108-1125.
[https://doi.org/10.1016/j.rser.2014.07.127]

- Ministry of Economy and Finance, “2050 carbon neutral strategy of the republic of Korea”, Ministry of Economy and Finance, 2020. Retrieved from https://www.korea.kr/archive/expDocView.do?docId=39241, .
-
H. W. Lee, D. H. Oh, and Y. J. Seo, “Prediction of changes in filling time and temperature of hydrogen tank according to SOC of hydrogen”, Trans Korean Hydrogen New Energy Soc, Vol. 31, No. 4, 2020, pp. 345-350.
[https://doi.org/10.7316/KHNES.2020.31.4.345]

-
B. H. Park, “Simulation of temperature behavior in hydrogen tank during refueling using cubic equations of state”, Trans Korean Hydrogen New Energy Soc, Vol. 30, No. 5, 2019, pp. 385-394.
[https://doi.org/10.7316/KHNES.2019.30.5.385]

-
C. J. B. Dicken and W. Mérida, “Modeling the transient temperature distribution within a hydrogen cylinder during refueling”, J. Numerical Heat Transfer Part A, Vol. 53, No. 7, 2007, pp. 685-708.
[https://doi.org/10.1080/10407780701634383]

-
A. Suryan, H. D. Kim, and T. Setoguchi, “Three dimensional numerical computations on the fast filling of a hydrogen tank under different conditions”, Int. J. Hydrogen Energy, Vol. 37, No. 9, 2012, pp. 7600-7611.
[https://doi.org/10.1016/j.ijhydene.2012.02.019]

- ANSYS, “2020 ANSYS FLUENT solver theory”, 2020. Retrieved from https://ansyshelp.ansys.com/account/secured?returnurl=/Views/Secured/corp/v201/en/flu_th/flu_th.html?q=ansys%20fluent%20theory%20guide, .
-
O. Redlich and J. N. S. Kwong, “On the thermodynamics of solutions. V. An equation of state. Fugacities of gaseous solutions”, Chem. Rev. Vol. 44, No. 1, 1949, pp. 233-244.
[https://doi.org/10.1021/cr60137a013]

- W. C. Kim, “Modern statistical”, 4th ed. YONUNGCHI MUNHWASA, Korea, 2006, pp. 256-325.