냉각계통 동적 예측을 위한 수전해 시스템 동적 모사 모델
2021 The Korean Hydrogen and New Energy Society. All rights reserved.
Abstract
Water electrolysis technology, which generates hydrogen using renewable energy resources, has recently attracted great attention. Especially, the polymer electrolyte membrane water electrolysis system has several advantages over other water electrolysis technologies, such as high efficiency, low operating temperature, and optimal operating point. Since research that analyzes performance characteristics using test bench have high cost and long test time, however, model based approach is very important. Therefore, in this study, a system model for water electrolysis dynamics of a polymer electrolyte membrane was developed based on MATLAB/Simulink®. The water electrolysis system developed in this study can take into account the heat and mass transfer characteristics in the cell with the load variation. In particular, the performance of the system according to the stack temperature control can be analyzed and evaluated. As a result, the developed water electrolysis system can analyze water pump dynamics and hydrogen generation according to temperature dynamics by reflecting the dynamics of temperature.
Keywords:
PEMWE, Transient response, Electroosmotic force, Back-diffusion, BOP, Activation overvoltage키워드:
고분자 전해질막 수전해, 과도현상, 전기 삼투 현상, 역확산, 보조 장치, 활성화 과전압1. 서 론
고분자 전해질막 수전해(proton electrolyte membrane water electrolyzer, PEMWE)는 신재생 에너지 자원으로부터 수소를 생성하는 데 가장 유리한 기술 중 하나로 간주된다1). 기술 성숙도가 짧음에도 불구하고 PEMWE는 다른 수전해 기술에 비해 많은 장점(단순성, 더 높은 전류 밀도, 고체 전해질, 더 높은 작동 압력)을 가지고 있어 기존 알칼리인 수전해를 대신하는 저온형 시스템에 사용되는 미래 대안이 될 것으로 예상된다. 최근 PEMWE에 관한 주요한 연구들은 PEMWE 기술의 잠재력을 보여준다2-7). 신재생 에너지와 PEMWE 결합으로 인해 많은 장점을 갖게 되는데 위험한 액체 전해질과 이를 재순환하고 제어하는 여러 부가 장치가 필요하지 않아 시스템이 간단해진다. 또한, 부하에 따른 빠른 대응으로 인해 시스템의 시동이 쉬워지며 높은 전류 밀도로 운전이 가능함에 따라 시스템의 소형화가 가능하다.
수전해 모델링은 수소 발생 시스템의 거동을 시뮬레이션하고 예측하는 데 아주 유용하다. 신재생 에너지와 수소 발생 시스템 구성 시 간헐적이고 가변적인 전력 공급을 예상할 수 있으므로 수전해 모델링은 신재생 에너지로부터 전력을 직접 공급받는 경우 더욱 더 중요한 역할을 할 수 있다.
지난 몇 년 동안 PEMWE 연구에 관한 관심이 눈에 띄게 증가하였으며 최근 몇몇 눈길을 끄는 PEMWE 모델들이 개발되었다. Choi 등8)은 Butler-Volmer 동역학을 기반으로 간단한 모델을 개발하였지만, 전기 화학적 거동만 다루었다. Görgün9)은 양극과 음극의 몰 균형 보존에 기반을 둔 완전한 동적 모델을 소개하였지만, 실험적으로 검증되지 않았다. 미국 노스다코타 대학(University of North Dakota)의 한 그룹은 준 경험식 방정식을 사용하여 6 kW PEMWE의 분극 성능을 모델링하였다10-12). 이 방정식은 열역학 이론과 Bulter–Volmer 역학을 기반으로 한다. 실험 피팅 결과에서 그들은 또한 전극의 교환 전류 밀도, 고분자 전해질막의 전도도 및 양극 전달계수 온도에 대한 영향을 분석하였다. 최근 Marangio 등13,14)은 고압 PEMWE를 통해 검증된 완전한 모델을 제시하였다. 그들의 연구는 농도 손실을 고려하였으며, 물질들은 수전해 전지들 내부로 흐르며 전극과 플레이트 그리고 막의 옴 손실 모델링을 복잡하게 한다. Lebbal과 Lecoeuche15)의 방식은 반응의 동역학을 모델링하기위한 농도 과전압을 고려하고 모델의 매개 변수를 추정하기 위한 비선형 제곱식별 방법을 제안한다. 변수들의 온도 의존성은 명확하지 않지만, 이 연구에서 사용된 구별법 및 모니터링 방법은 아주 흥미롭다. Awasthi 등16)은 온도와 압력 변화가 전지 성능과 손실에 미치는 영향을 조사하였다. Lee 등17)은 PEMWE의 성능에 대한 온도, 유속 및 유동장의 영향을 조사하기 위해 PEMWE 모델을 개발하고 그 결과를 실험적 연구와 비교하였다. Han 등18)은 PEMWE에서 확산 손실을 계산할 수 있는 전기 화학 모델을 개발하였다. Abdin 등19)은 또한 전기 회로 모델로 전해조의 옴 저항을 나타내기 위해 Simulink를 사용하는 PEMWE 모델을 개발하였다. 그들은 또한 PEMWE 성능에 대한 온도와 압력의 영향을 조사하고 그 결과를 먼저 수행된 실험 결과와 비교하였다.
대부분의 모델링 연구는 주로 셀 또는 스택의 형상 또는 거동에 중점을 둔다. 시스템을 설계할 때는 운전 조건에 따른 PEMWE의 거동이 연구되어야 한다. 또한, 셀 또는 스택의 최적화된 변수들을 사용하여 시스템을 구축하는 것도 매우 중요하다. 때로는 셀 또는 스택의 운전 변수들이 다른 시스템 구성품들의 특성에 따라 변경되어야 한다. 시스템의 구성 요소 및 정격 조건 범위를 결정할 때 전원 공급 장치, 물 펌프, 물탱크, 냉각 시스템, 제어 장치 등과 같은 여러 구성 요소의 특성도 고려되어야 한다. 연료전지에 관한 다양한 시스템 모델링 연구가 있다20-26). 그러나 PEMWE 스택을 포함한 시스템 모델링에 관한 연구는 문헌상 찾기 힘들다. Dale 등12)은 상용화된 시스템 내의 PEMWE 스택을 모델링하였지만 시스템 구성품 모델을 포함하지 않았다. 이런 시스템들은 가동 중 외부 환경 조건 및 이전 조건에 따라 운전 조건을 지속해서 바꿔야 한다. 또한, PEMWE 시스템은 운전 온도에 따라, 냉각 조건에 따라 시스템 성능이 급격하게 변한다. 그러므로 시스템 모델 구성품 간의 통합과 이에 따른 운전 최적화 및 온도 최적화가 필수이다. 또한 수전해 시스템을 실제 사양으로 구축하기에는 상당히 큰 비용이 필요하며 시스템을 운전하는 데에도 수 시간이 필요하다. 하지만 본 연구처럼 수전해 시스템의 외부환경 및 과도현상, 전체적인 BOP를 통합한 수전해 시스템을 Matlab/Simulink로 구축하게 되면 이러한 단점들을 보안할 수 있다. 또한, 수소의 발생량이 전류 및 온도의 영향을 받기 때문에 적절한 스택의 온도제어를 통해 수전해 시스템의 더욱 높은 효율을 도출해 낼 수 있다.
따라서 본 연구에서는 MATLAB/Simulink를 기반으로 PEMWE 동특성 시스템 모델을 개발하였다. 시스템 내의 각 부품 모델을 개발하여 스택 모델과 통합하고 전체 PEMWE 시스템의 동적 응답특성을 분석할 수 있도록 개발하였다. 또한, 부하 변화에 따른 각 수전해 셀 내의 열 및 물질 전달 특성을 고려할 수 있도록 모델링 하였다. 이에 따라 전해질막의 동특성 및 시스템 전체의 동특성을 파악할 수 있도록 열관리 모델이 개발되었다. 이를 이용하여 시스템에 인가되는 전압, 전류 및 운전 온도 등의 변화에 따른 수소 발생량을 제어할 수 있고, 운전 최적화를 통해 시스템 효율을 최대로 끌어올릴 수 있다.
2. 본 론
2.1 고분자 전해질 수전해 해석 모델
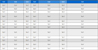
수전해 시스템은 물의 전기분해 반응 때문에 수소와 산소를 발생한다. 이러한 전기분해 반응을 자세히 설명하기 위해서는 과도현상(transient response)을 포함한 정교한 모델을 필요로 한다. 그 중 수전해 시스템에 대한 다양한 모델들이 보고되고 있으나 대부분 모델은 과도현상을 고려하지 않은 정상 상태를 가정한 수학적 모델이다. 이러한 모델은 동적 응답특성에 대한 전체 시스템의 응답특성을 정확히 분석할 수 없으며, 부하 변화에 따른 셀 내의 열 및 물질 전달 특성을 분석할 수 없다. 이에 전해액의 동특성 및 시스템 전체의 동특성을 반영하기 위한 열 모델 및 열관리 모델이 필요하다. 본 연구에서는 수전해 시스템을 개발하기 위해, 연료극, 공기극, 막 전해질 등으로 스택 모델을 구성하였으며, 펌프, 열 교환기 그리고 모터 등으로 보조 장치를 구성하였다. Table 1은 본 연구에 사용된 수전해 스택의 사양과 작동 온도를 나타낸다.
2.2 연료극 ancillary
연료극은 산소와 막-전극 표면에서 전기 화학 반응으로 발생한 산소 가스 모델을 계산할 수 있다.
| (1) |
| (2) |
Xi는 종의 몰 분율이며, nO2는 산소의 몰 유동, 는 연료극을 통한 물의 몰 유동이다.
2.3 공기극 ancillary
공기극은 물의 전기 화학 반응 때문에 막-전극 표면에 수소가 생성되며, 연료극과 계산과정이 유사하다.
| (3) |
| (4) |
nH2는 수소의 몰 유동, 는 공기극에서 물의 몰 유동이다.
2.4 Membrane ancillary
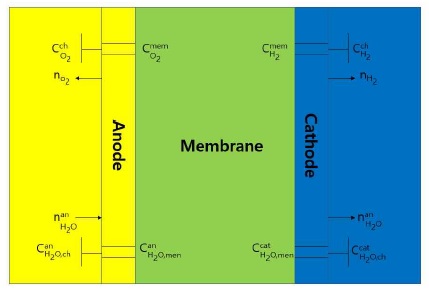
전기삼투현상과 역 확산력에 의한 습증기 함유도(water content, λ)는 이온 교환막 전해질의 습증기 수송특성과 전기전도도와 상관관계를 확인할 수 있다. Fig. 1은 고분자 전해질막 전해액 셀 내부의 각 화학종의 농도 및 몰 유동을 설명한다.
수전해 막내의 물 수송 보존 방정식은 다음과 같다.
| (5) |
여기서, , 는 전기삼투압, 역확산 현상에 의한 질량 유량이다
전기삼투압 저항계수(nd)는 양성자당 이동하는 물의 몰수와 물 함유도를 통해 정의된다.
| (6) |
역확산력은 결과적으로 막 전체에 걸친 물 농도를 균일하게 유지할 수 있으며 막을 통한 물의 이동 유량은 다음과 같이 표현할 수 있다.
| (7) |
여기서 nd은 전기삼투압의 저항계수이고, Dw는 막 내에서 물의 확산계수이며, δmem는 막의 두께, ρH2O는 물의 밀도이다. Tan,Tcat는 연료극과 공기극의 채널로 유입되는 가스의 온도, M>H2O는 물의 분자량이다. 또한 는 2항 (H2-H2O)의 연료극에서의 유효확산계수이고, 는 공기극에서의(O2-H2O) 유효확산계수이며, , 는 연료극과 공기극에서의 채널 두께를 각각 나타낸다.
2.5 수전해 시스템 전압 모델
상용화된 전해질은 전류를 제어하여 필요한 작동전압을 준수해야 한다. 본 연구에서는 전류를 입력으로 전압을 출력으로 설정하였으며, 일반적으로 수전해 시스템 셀에 인가되는 전압 및 셀 내에서의 전압은 다음과 같이 가역 전압에 각각의 손실을 추가해준 값으로 계산할 수 있다.
| (8) |
ENernst은 Nernst 전압이고, Vact,a,Vact,c은 연료극, 공기극 활성화 과전압이며, VΩ은 이온 전도성 및 전기적 저항 과전압, Vcon는 스택 내에서의 농도 과전압이다.
활성화 과전압은 전기 화학 운동성 및 전극 표면에서 일어나는 반응속도를 나타내며 다음과 같이 유도된다.
| (9) |
여기서 io는 교환 전류 밀도이며, αan,αcat는 연료극, 공기극 전하 전달계수이다.
전기분해가 진행 중일 때 전극 표면에서는 반응물질의 농도변화로 인해 농도/전위성이 발생하여 반응률이 저하된다. 일반적으로 농도 저항은 수전해 시스템의 작동조건에 벗어나는 영역이기 때문에 고려하지 않아도 되지만, 본 연구에서는 향후 농도 손실에 따른 내구성을 분석하기 위해 다음과 같이 유도하였다.
| (10) |
| (11) |
여기서 , 는 막과 전극 인터페이스에서의 산소와 수소 농도이며, Deff는 수송 매체의 유효 확산계수이다.
수전해 시스템이 작동하면 셀 내에서 전하의 이동으로 인해 손실이 발생하며 이를 저항 손실이라고 한다. 저항 손실은 막의 두께, 전도도 그리고 셀의 작동 온도의 상관관계로 표현되며, 다음과 같다.
| (12) |
여기서 λ은 막의 물 함유도를 나타내며, 일반적인 수전해 시스템에서는 물을 유입 유체로 사용하기 때문에 완전 포화상태를 가정하여 함유도를 22로 설정하였다
수전해 시스템에서 발생하는 열을 계산하기 위해서는 이론적인 전압에서 손실들을 모두 제거한 실제 전압을 구해야 한다. 또한, 수전해 시스템은 전극에 전류를 가해서 수소를 생산함과 동시에 열을 발생시키므로, 유입물이 수소 생성과 방열 역할을 동시에 하게 된다. 스택 내에서 발생한 모든 열이 냉각수에 모두 열이 전달된다고 가정하면 냉각수 출구 온도는 스택 온도와 동일하게 된다. 따라서 냉각수 출구 온도와 방열량은 다음과 같다.
| (13) |
| (14) |
2.6 냉각수 저장조(reservoir) 모델
전술하였듯이, 수전해 시스템의 경우 유입되는 물이 냉각수의 역할도 하므로 냉각수 저장조가 필요하다. 또한, 저장조의 물의 양에 따라 전체 시스템의 온도 응답 시정 수에 끼치는 영향력이 상당하기에 이를 설명하기 위한 모델이 필요하다. 레저버 모델은 단열 용기 모델로 가정하였으며 냉각수의 용량은 사용자의 입력에 의해 변경할 수 있도록 설계되었다.
| (15) |
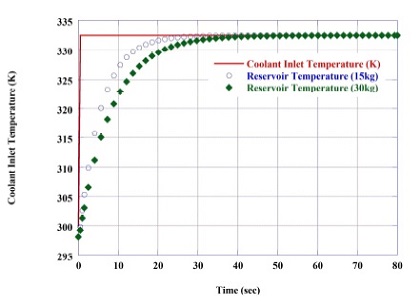
Fig. 2는 잔류유량을 15 kg과 30 kg을 기준으로 해석한 결과이다. 30 kg의 잔류유량에 비해 15 kg의 잔류유량을 선정한 결과가 대략 10초 정도 감소하였으며 여전히 응답에 많은 시간을 소요함을 알 수 있었다. 본 연구에서는 스택과 펌프 사이에 레저버가 위치하는 것으로 모델링하였다.
2.7 모터 동적 거동 모델
직류 전동기는 부하에 에너지를 제공하는 전력 구동 소자이며 전달함수는 본 연구에서는 모터 다이나믹스를 고려하였다. 하지만 비선형 모터 모델은 계산 부하를 증가시켜 다음과 같은 전달함수의 형태로 표현하여 적용하였다.
| (16) |
여기서 시정 수를 τf=Lf/Rf,τL=J/b이라 하고, Km은 전동기 상수이다.
2.8 열 교환기 단순 모델
열 교환기 모델의 복잡성은 수전해 시스템 모델 설계에서 방해가 되기 때문에 열 교환량만 계산할 수 있는 수준으로 단순화하였으며 특성은 유지해야 한다. 따라서 열교환기 모델은 입구 온도 정보를 바탕으로 그 유효도를 찾아 적용하여 모델링 하였다.
| (17) |
3. 결과 및 고찰
3.1 스택 동특성 모델 검증
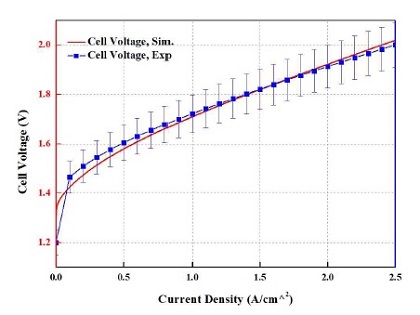
본 연구에서는 개발된 모델의 검증을 수행하기 위해 참고문헌 데이터를 활용하였다. 차후 모듈 검증을 위한 수전해 시스템 성능 평가 장치를 구성하고 획득한 시험 데이터를 활용할 예정이다. 단위 전지 특성 평가는 290 cm2의 활성화 면적을 가지고 셀을 구성하였다. Fig. 3에서 보듯이, 개발된 수전해 시스템 스택 전압 모델이 참고문헌 데이터와 오차 범위 5% 이내에 잘 설명하는 것을 확인할 수 있다.
3.2 정전류 입력 시 전압
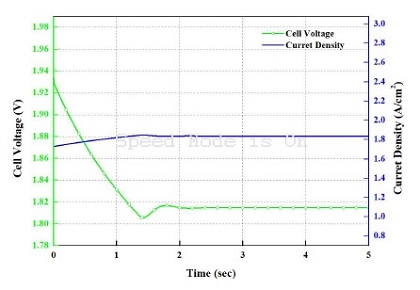
Fig. 4는 정전류에 따른 수전해 시스템 전압을 나타낸다. 여러 전류 밀도 영역을 가지고 있는 수전해 시스템은 넓은 전압 영역을 가지고, 정전류 시뮬레이션은 약 1.88 V 영역에서 진행되었다. Fig. 4에 나타내어진 수전해 시스템 정전류 테스트에서는 전류 입력에 따른 수전해 시스템의 전압을 확인할 수 있다.
또한, 온도 동특성을 고려한 모델이기 때문에 온도 동특성에 따라 전압값이 동특성을 가진다는 것을 볼 수 있다.
3.3 온도 동특성
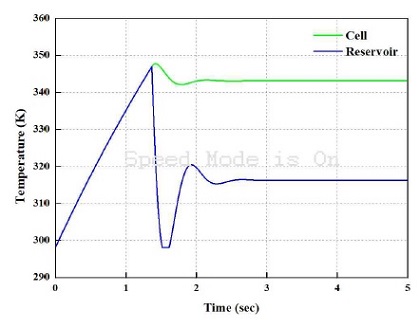
Fig. 5는 각각 본 연구에서 설정한 스택 온도와 2차 냉각수의 입구 온도(레저버 온도)를 임의로 설정한 정전류 프로파일로 시스템을 구동하였을 시의 온도 응답성을 나타낸 것이다.
Fig. 5에서 스택의 온도값은 지령값이 70℃에 수렴하는 것을 확인할 수 있으며, 이는 PI 제어 기법으로 설계된 피드백 제어 기법이 정상적으로 작동하는 알 수 있으며, 온도의 동특성을 모델에 제대로 반영되었다는 것을 알 수 있다. 또한, 수전해 시스템으로 유입되는 2차 냉각라인의 냉각수의 온도 응답도 설정한 제어 지령에 수렴하는 것을 알 수 있다. 비록 오버 슈트와 다운 슈트가 어느 정도 존재하지만, 향후 실험 결과값을 바탕으로 튜닝 게인을 조정한다면 견실한 제어기에 따른 정확한 온도 예측을 할 수 있을 것이라 사료된다.
3.4 BOP 동특성
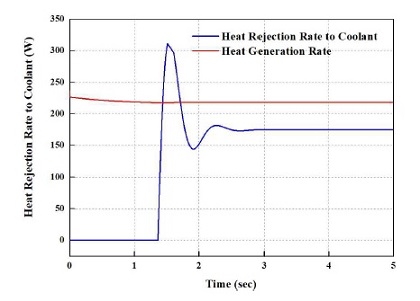
Fig. 6은 각각 연료전지 셀 내에서 전기 화학 반응 때문에 발생한 열 및 냉각수로의 열전달 양을 나타낸 것이다. 정전류를 수전해 시스템이 인가하였기 때문에, 셀 내의 전기 화학 반응은 온도 변화에 지배적이다. 따라서 Fig. 6에서와 같이, 셀 내의 열 발생량은 약 230 W에서 초기 조건에 발열이 되어 시간이 지나갈수록 거의 변화가 없게 된다. 일반적으로 수전해 시스템은 효율이 가장 좋은 영역에서 정전류로 작동하므로, BOP를 포함한 전체 연료전지 시스템을 최적 통합하여 효율이 가장 좋은 영역을 도출하고 작동조건을 설정한 후 시스템을 구동하게 된다면, 수전해 시스템의 효율을 극대화할 수 있으리라 생각된다. 이러한 작업을 위해서는 개발된 모델의 실험적 검증이 충분히 이루어져야 한다. 또한, 펌프에 의해 유입되는 냉각수는 두 가지 일을 병행한다. 첫 번째로 수소를 발생시키며, 두 번째는 셀 내에 발생한 열을 적절히 제거해 준다. Fig. 6에서 보듯이, 셀 내의 열 발생을 적절히 제거해 주고, 셀 내의 온도를 제어하기 위해 적절히 열을 제거해 주는 것을 볼 수 있다. 다운 슈트와 오버 슈트가 존재하는 것은 냉각수 유량 유입의 제어를 위해 PI 제어기를 모델에 추가하였기 때문이다.
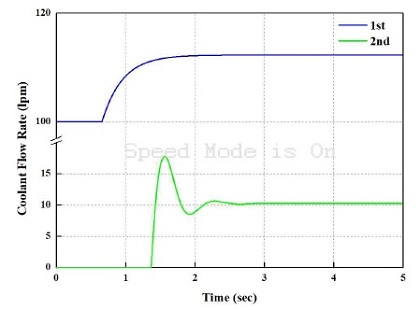
이는 Fig. 7에서 더 자세히 확인할 수 있다. Fig. 7에서 보면 1차로 셀 내에 유입되는 냉각수의 유량은 초기에 100 lpm으로 유입되지만, 정전류가 셀로 인가되었을 때, 열 발생량을 제거하기 위해 유량이 증가하는 것을 볼 수 있다. 유량은 약 110 lpm 정도로 냉각을 위해 증가되며, 이에 맞추어 셀에서의 냉각수로의 열 전달량이 Fig. 6에서와 같이 증가한다. 또한, 열 교환기에 설치된 2차 측 펌프의 유량도 확인할 수 있다. 1차로 셀 내에 발생한 열을 얻은 냉각수는 셀 내의 채널 출구에서 온도가 증가하게 된다. 증가한 냉각수를 적절히 냉각하고 다시 셀 내에 유입하기 위해서는 열 교환기에 의해 냉각이 되어야 한다. 열 교환기의 방열을 위해서는 2차 측 펌프 모델이 추가로 더 필요한데, 이는 스택으로 유입하는 냉각수의 방열을 담당하는 역할을 한다.
Fig. 7에서 보면 스택으로 유입되는 1차 측 펌프 출구 유량과 열 교환기로 유입되는 2차 측 펌프 유량을 볼 수 있다. 스택의 방열을 위해 1차 측 출구의 유량이 증가하면 어느 정도의 시차를 가지고 2차 측 열 교환기의 유량이 증가하는 것을 볼 수 있다. 이는 스택의 열량이 증가하면 방열을 위한 1차 측 펌프 유량이 증가하고, 따라서 1차 측 냉각수의 방열을 위한 2차 측 펌프의 유량이 증가한다.
3.5 수소 발생량
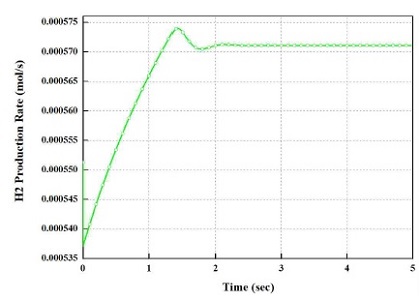
Fig. 8은 정전류 입력에 따른 셀 내의 수소 발생량을 나타내었다. 채널 내의 초기에 저장된 수소의 양은 0.000552 mol이라 가정하였다. Fig. 8에서 보듯이,
시뮬레이션 초기에 초기 조건에서 서서히 증가하여 약 2초에 정상 상태가 되는 것을 볼 수 있다. 이는 수소의 발생량이 전류 및 온도의 영향을 받기 때문이다. 특히, 전압의 경우 막 또는 전극의 저항 그리고 열전도도가 온도에 지배적으로 영향을 받는다. 활성화 과전압도 온도에 영향을 받지만, 특히 저항 손실에서 온도의 영향을 많이 받기 때문에, 적절한 스택의 온도제어는 수전해 시스템의 효율을 보장할 수 있다. 이러한 영향을 모델에 반영하였기 때문에, 수소 발생량에 있어 동특성 현상을 볼 수 있다. 일반적으로 26 kW 이상의 수전해 시스템은 정상상태 도달까지 수 시간이 걸리지만, 모델의 동특성만을 확인 하기 위해 열용량 및 시정 수를 작게 설정하였다. 향후 모델 검증 테스트 장비와 비교 검증하여 모델의 정교화를 높일 예정이다.
4. 결 론
온도의 동특성이 반영된 모델을 개발하였으며 결과적으로 수소 발생량의 동특성 현상을 확인하였다.
1) 전기분해 반응의 과도현상을 포함한 정교한 모델을 개발하였으며 보조 장치 또한 개발 및 통합하였다.
2) 정전류 입력 시 온도 동특성을 고려한 모델로 온도 동특성에 따른 전압값의 동특성을 확인하였다. 또한 온도 동특성 PI제어기법으로 설계된 피드백 제어 기법이 정상적으로 운전하는 것을 확인하였다.
3) BOP를 포함한 전체 연료전지 시스템을 최적 통합하여 효율이 가장 좋은 영역을 작동조건으로 설정하여 시스템을 구동 시 수전해 시스템의 효율을 극대화할 수 있다.
4) 수소의 발생량은 전류 및 온도의 영향을 받으며 전압의 경우 저항손실에서 온도의 영향이 크기 때문에 적절하게 스택의 온도를 제어 한다면 수전해 시스템의 효율은 증가시킬 수 있다.
Acknowledgments
본 연구는 교육부(한국연구재단)의 지자체-대학협력기반 지역혁신 사업(경상남도지역혁신플랫폼 스마트제조엔지니어링)으로 수행되었습니다.
References
-
F. Barbir, “PEM electrolysis for production of hydrogen from renewable energy sources”, Solar Energy, Vol. 78, No. 5, 2005, pp. 661-669.
[https://doi.org/10.1016/j.solener.2004.09.003]

-
J. Turner, G. Sverdrup, M. K. Mann, P. C. Maness, B. Kroposki, M. Ghirardi, R. J. Evans, and D. Blake, “Renewable hydrogen production”, Int. J. Energy Res., Vol. 32, No. 5, 2007, pp. 379-407.
[https://doi.org/10.1002/er.1372]

-
P. Millet, R. Ngameni, S.A. Grigoriev, N. Mbemba, F. Brisset, A. Ranjbari, and C. Etiévant, “PEM water electrolyzers: from electrocatalysis to stack development”, Int. J. Hydrogen Energy, Vol. 35, No. 10, 2010, pp. 5043-5052.
[https://doi.org/10.1016/j.ijhydene.2009.09.015]

-
P. Millet, N. Mbemba, S. A. Grigoriev, V. N. Fateev, A. Aukauloo, and C. Etiévant, “Electrochemical performances of PEM water electrolysis cells and perspectives”, Int. J. Hydrogen Energy, Vol. 36, No. 6, 2011, pp. 4134-4142.
[https://doi.org/10.1016/j.ijhydene.2010.06.105]

-
S. A. Grigoriev, V. I. Porembskiy, S. V. Korobtsev, V. N. Fateev, F. Auprêtre, and P. Millet, “High-pressure PEM water electrolysis and corresponding safety issues”, Int. J. Hydrogen Energy, Vol. 36, No. 3, 2011, pp. 2721-2728.
[https://doi.org/10.1016/j.ijhydene.2010.03.058]

-
P. Millet, R. Ngameni, S. A. Grigoriev, and V. N. Fateev, “Scientific and engineering issues related to PEM technology: water electrolysers, fuel cells and unitized regenerative systems”, Int. J. Hydrogen Energy, Vol. 36, No. 6, 2011, pp. 4156-4163.
[https://doi.org/10.1016/j.ijhydene.2010.06.106]

-
J. Nieminen, I. Dincer, and G. Naterer, “Comparative performance analysis of PEM and solid oxide steam electrolysers”, Int. J. Hydrogen Energy, Vol. 35, No. 20, 2010, pp. 10842-10850.
[https://doi.org/10.1016/j.ijhydene.2010.06.005]

-
P. Choi, D. G. Bessarabovb, and R. Dattaa, “A simple model for solid polymer electrolyte (SPE) water electrolysis”, Solid State Ionics, Vol. 175, No. 1-4, 2004, pp. 535-539.
[https://doi.org/10.1016/j.ssi.2004.01.076]

-
H. Görgün, “Dynamic modelling of a proton exchange membrane (PEM) electrolyzer”, Int. J. Hydrogen Energy, Vol. 31, No. 1, 2006, pp. 29-38.
[https://doi.org/10.1016/j.ijhydene.2005.04.001]

-
C. Y. Biaku, N. V. Dale, M. D. Mann, H. Salehfar, A. J. Peters, and T. Han, “A semiempirical study of the temperature dependence of the anode charge transfer coefficient of a 6 kW PEM electrolyzer”, Int. J. Hydrogen Energy, Vol. 33, No. 16, 2008, pp. 4247-4254.
[https://doi.org/10.1016/j.ijhydene.2008.06.006]

-
K. W. Harrison, E. Hernandez-Pacheco, M. Mann, and H. Salehfar, “Semiempirical model for determining PEM electrolyzer stack characteristics”, J. Fuel Cell Sci. Technol., Vol. 3, No. 2, 2006, pp. 220-223.
[https://doi.org/10.1115/1.2174072]

-
N. V. Dale, M. D. Mann, and H. Salehfar, “Semiempirical model based on thermodynamic principles for determining 6 kW proton exchange membrane electrolyzer stack characteristics”, Journal of Power Sources, Vol. 185, No. 2, 2008, pp. 1348-1353.
[https://doi.org/10.1016/j.jpowsour.2008.08.054]

-
F. Marangio, M. Santarelli, and M. Cali, “Theoretical model and experimental analysis of a high pressure PEM water electrolyser for hydrogen production”, Int. J. Hydrogen Energy, Vol. 34, No. 3, 2009, pp. 1143-1158.
[https://doi.org/10.1016/j.ijhydene.2008.11.083]

-
M. Santarelli, P. Medina, and M. Cali, “Fitting regression model and experimental validation for a high-pressure PEM electrolyzer”, Int. J. Hydrogen Energy, Vol. 34, No. 6, 2009, pp. 2519-2530.
[https://doi.org/10.1016/j.ijhydene.2008.11.036]

-
M. E. Lebbal and S. Lecoeuche, “Identification and monitoring of a PEM electrolyser based on dynamical modelling”, Int. J. Hydrogen Energy, Vol. 34, No. 14, 2009, pp. 5992-5999.
[https://doi.org/10.1016/j.ijhydene.2009.02.003]

-
A. Awasthi, K. Scott, and S. Basu, “Dynamic modeling and simulation of a proton exchange membrane electrolyzer for hydrogen production”, Int. J. Hydrogen Energy, Vol. 36, No. 22, 2011, pp. 14779-14786.
[https://doi.org/10.1016/j.ijhydene.2011.03.045]

- B. Lee, K. Park, and H. Kim, “Dynamic simulation of PEM water electrolysis and comparison with experiments”, Int. J. Electrochem. Sci., Vol. 8, 2013, pp. 235-248. Retrieved from http://electrochemsci.org/papers/vol8/80100235.pdf, .
-
B. Han, S. M. Steen, J. Mo, and F. Y. Zhang, “Electrochemical performance modeling of a proton exchange membrane electrolyzer cell for hydrogen energy”, Int. J. Hydrogen Energy, Vol. 40, No. 22, 2015, pp. 7006-7016.
[https://doi.org/10.1016/j.ijhydene.2015.03.164]

-
Z. Abdin, C. J. Webb, and E. M. Gray, “Modelling and simulation of a proton exchange membrane (PEM) electrolyser cell”, Int. J. Hydrogen Energy, Vol. 40, No. 39, 2015, pp. 13243-13257.
[https://doi.org/10.1016/j.ijhydene.2015.07.129]

-
K. Haraldsson and K. Wipke, “Evaluating PEM fuel cell system models”, Journal of Power Sources, Vol. 126, No. 1-2, 2004, pp. 88-97.
[https://doi.org/10.1016/j.jpowsour.2003.08.044]

-
P. R. Pathapati, X. Xue, and J. Tang, “A new dynamic model for predicting transient phenomena in a PEM fuel cell system”, Renewable Energy, Vol. 30, No. 1, 2005, pp. 1-22.
[https://doi.org/10.1016/j.renene.2004.05.001]

-
A. J. del Real, A. Arce, and C. Bordons, “Development and experimental validation of a PEM fuel cell dynamic model”, Journal of Power Sources, Vol. 173, No. 1, 2007, pp. 310-324.
[https://doi.org/10.1016/j.jpowsour.2007.04.066]

-
C. Wang, M. H. Nehrir, and S. R. Shaw, “Dynamic models and model validation for PEM fuel cells using electrical circuits”, IEEE Transactions on Energy Conversion, Vol. 20, No. 2, 2005, pp. 442-451.
[https://doi.org/10.1109/TEC.2004.842357]

-
G. L. Arsov, “Improved parametric PSpice model of a PEM fuel cell”, 2008 11th International Conference on Optimization of Electrical and Electronic Equipment, 2008, pp. 203-208.
[https://doi.org/10.1109/OPTIM.2008.4602367]

- C. Spiegel, “PEM fuel cell modeling and simulation using Matlab”, Academic Press/Elsevier, USA/Netherlands, 2008.
-
A. C. Olesen, C. Rømer, and S. K. Kær, “A numerical study of the gas-liquid, two-phase flow maldistribution in the anode of a high pressure PEM water electrolysis cell”, Int. J. Hydrogen Energy, Vol. 41, No. 1, 2016, pp. 52-68.
[https://doi.org/10.1016/j.ijhydene.2015.09.140]